Introduction
Global averages of glacier mass balance (Reference Kaser, Cogley, Dyurgerov, Meier and OhmuraKaser and others, 2006) are based mostly on direct measurements, which support reasonably convincing estimates at annual (Oh-mura, 2004; Reference Dyurgerov and MeierDyurgerov and Meier, 2005) or pentadal (Reference Cogley and AndersonCogley, 2005) resolution. These data leave much to be desired in terms of coverage. One way to improve coverage would be to draw on geodetic as well as direct measurements. However, before we can treat direct and geodetic balance measurements within the same analytical framework, we must address the mismatch in temporal resolution. Direct measurements are nearly all annual, whereas geodetic measurements are nearly all multi-annual. The aims of this paper are therefore to: (1) describe a new compilation of geodetic mass-balance measurements; (2) compare all available direct–geodetic measurement pairs so as to identify possible biases; (3) develop a common analytical framework for diverse balance measurements; and (4) present updated estimates of global balance based on the new compilation.
For compactness, annual whole-glacier mass balance is denoted here as b, without distinguishing the method of measurement, and as d or g when we need to make clear that the measurement is direct or geodetic, respectively. Estimates for n-year spans, with n≥1, are denoted by B, D or G, and variances by σi 2, with 〉 standing for b, d or g.
Available Data
Geodetic balance measurements were assembled from just over 100 published sources. Most are single; only 40% of the glaciers have more than one measurement. The distribution of measurement spans is very wide, with many covering several decades. However, the number of glaciers with geodetic measurements is not very different from the number with direct measurements (Table 1). There are fewer than one-fifth as many geodetic as direct measurements, although they cover four times as many balance years. They also cover more calving glaciers, in proportions likely to be closer to the (unknown) ideal, than do direct measurements. Two-fifths of glaciers with more than one geodetic measurement probably exhibit more rapid loss recently than earlier, a somewhat smaller fraction than for glaciers with direct measurements.
Table 1. Comparison of direct and geodetic mass-balance datasets
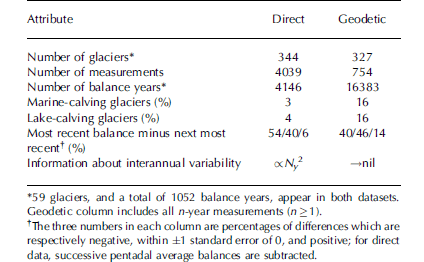
The main message of Table 1, reinforced by Figure 1, is that we could realize a dramatic increase in data density, measured in balance years, if we could remedy the absence of information about temporal variability in multi-annual measurements.

Fig. 1. Distribution of geodetic (G) and direct (D) measurements over time. Each geodetic measurement contributes up to five balance years to each of the pentads which it spans.
Figure 2 summarizes the evolution of mass balance since 1860. Figure 2a confirms that mass balance has recently become more negative, although this might result from wider geodetic sampling. Figure 2b is subject to the same possible sampling problems as Figure 2a but, at face value, it is encouraging because, despite the smoothing of G, the two methods agree in showing a relative maximum near 1970 and an accelerating decrease since then. However, G is distinctly more negative than D, which should lead us to expect reduced estimates when the two are combined and corrected for spatial bias. A recent estimate of the evolution of mass balance since the 19th century (Reference Oerlemans, Dyurgerov and van de WalOerlemans and others 2007), based on measurements of terminus fluctuations, lies in between the arithmetic-average series of D and G, which strengthens this expectation.

Fig. 2. Evolution of geodetically measured mass balance. (Note different balance-axis scales.) (a) The measurements for each glacier are plotted as a time series; 30 of 678 measurements lie beyond the range of the balance axis. (b) Pentadal arithmetic averages over all measured glaciers of G (circles, open for pentads with fewer than 10 measurements) and D (triangles, open for pentads with fewer than 100 annual measurements). Multi-annual measurements are counted in each of the pentads which they span. Vertical bars represent ±2 standard errors of each pentadal sample about its arithmetic average. The irregular dark grey envelope is a rendering of the estimates of Reference Oerlemans, Dyurgerov and van de WalOerlemans and others 2007, (fig. 7).
Treatment of Data
The essential attributes of the direct-balance dataset have not changed since it was first described by Reference Cogley and AdamsCogley and Adams (1998). I concentrate here on the newly assembled geodetic data. In practice, there being seldom any in situ information about density, geodetic measurements approximate the average of specific mass change over time-span Δt by:
Glacier-wide average density ![]() is usually assumed to be 900 kgm–3. Lesser values are sometimes adopted, particularly when decreases of thickness are believed to involve losses of firn rather than of ice. I accept the authors’ value for
is usually assumed to be 900 kgm–3. Lesser values are sometimes adopted, particularly when decreases of thickness are believed to involve losses of firn rather than of ice. I accept the authors’ value for ![]() when one is given and assume that it is 900 kg m–3 when no value is given. A rare study in which uncertainties in
when one is given and assume that it is 900 kg m–3 when no value is given. A rare study in which uncertainties in ![]() are considered is that of Reference ØstremSapiano and others (1998). I adopt their suggested error of about 6% in mass balance due to the uncertainty in density.
are considered is that of Reference ØstremSapiano and others (1998). I adopt their suggested error of about 6% in mass balance due to the uncertainty in density.
Various methods, differing greatly in intrinsic accuracy and in completeness of sampling, have been applied to the estimation of areal-average thickness change ![]() The traditional method was to compute changes of elevation from contours on printed maps. Recently, it has become usual to take differences of digital elevation models or to extrapolate from surveyed traverses. When a standard error is given for
The traditional method was to compute changes of elevation from contours on printed maps. Recently, it has become usual to take differences of digital elevation models or to extrapolate from surveyed traverses. When a standard error is given for ![]() and is plausible, it is adopted without change; otherwise, a standard error of ±3.0 m is assumed. This is comparable with the uncertainties published by workers who have made careful analyses of their errors, and also allows for the lack of published information about seasonal corrections, the difficulty of mapping elevation over featureless snowfields and, for some methods, the uncertainty resulting from incomplete sampling. As is appropriate to the nature of the measurements, the error is not proportional to the amount of time between start and end surveys. The practice of representing glacier area by the average of starting and ending glacier areas, which is common but not invariable, is followed uniformly.
and is plausible, it is adopted without change; otherwise, a standard error of ±3.0 m is assumed. This is comparable with the uncertainties published by workers who have made careful analyses of their errors, and also allows for the lack of published information about seasonal corrections, the difficulty of mapping elevation over featureless snowfields and, for some methods, the uncertainty resulting from incomplete sampling. As is appropriate to the nature of the measurements, the error is not proportional to the amount of time between start and end surveys. The practice of representing glacier area by the average of starting and ending glacier areas, which is common but not invariable, is followed uniformly.
The time-span can be a source of significant uncertainty, especially when dates of early photography are in question or when imagery from more than one date is used to represent a single epoch. I record the uncertainty as a range, in days, and assume that the standard error of each date is half of the range. Thus, for example, dates given only to the nearest year have an uncertainty of half a year. Seasonal corrections are necessary when survey dates are not separated by an integer number of years. They restore the average surface elevation to a value appropriate to the beginning or end of the balance year, or to the date of the other survey. When given, they are adopted without change, except that they are assigned an uncertainty of ±20% if necessary. It is not practical to supply seasonal corrections when they are not given by authors. Indeed, it is often not possible to tell whether they are needed. It is commonly assumed that seasonal corrections are not necessary when the start and end dates are far apart. In fact, they become insignificant when measured thickness changes are large by comparison with the amplitude of the seasonal cycle of thickness, which is not the same thing.
The uncertainty in G is calculated, based on Equation (1), by conventional propagation of the standard errors of ![]()
![]() and Δt.
and Δt.
The standard error of annual d is estimated to be 200 kgm–2 a–1, following Reference Cogley and AdamsCogley and Adams (1998). This error grows at 10% a–1 for those few measurements that are multi-annual.
Direct–Geodetic Comparisons
Figure 3 shows that there is no evidence, at this scale of analysis, of systematic differences between D and G. The average difference, –74 kgm–2 a–1 or –0.09 standard errors, is negligible, but the spread is substantial. The root mean square of G–D is 378 kgm–2 a–1, but only 3% of the differences, all with D greater than G, are statistically significant. The best-fitting linear relationship between D and G has a slope (not shown) of dD/dG = 0.85±0.10, indicating that very negative G is associated with somewhat less negative D. (Unless stated otherwise, uncertainties are quoted as twice the standard error.) A physical explanation of this result remains to be identified, although it might be connected with the better representation of tidewater glaciers in the geodetic dataset. Much effort has gone into seeking explanations for observations of G–D. The new compilation offers an opportunity to assess reasons for the observed differences and to decide whether they have a physical rather than an instrumental basis; however, a more detailed approach than is possible here will be needed.

Fig. 3. Relationship between 105 coincident geodetic and direct mass-balance measurements, G and D respectively, from 29 glaciers. Five pairs, all with large uncertainties in G, lie beyond the range of the axes. Error bars represent ±1 standard error. Open symbols: measurements shorter than 3 years.
The open symbols in Figure 3 represent measurements spanning only 1 or 2 years. In the dataset as a whole, there are 40 such measurements of G, with an average standard error of 1372 kgm–2 a–1. This means that, in practice, they are not useful. Typical errors in ![]() and
and ![]() limit the temporal resolving power of geodetic methods to no better than ∽3 years.
limit the temporal resolving power of geodetic methods to no better than ∽3 years.
Variance Estimation For Multi-annual Balance Measurements
An n-year balance measurement can be seen as an average of a series of hypothetical annual measurements. It can also be seen as an estimate of each actual 1 year balance. The error due to natural variability, that is, the uncertainty in each annual balance g (estimated to be equal to G), is the standard deviation of the population of which the hypothetical series is a sample. For this claim to be valid, the annual series must be stationary and normally distributed with independent (roughly speaking, uncorrelated) elements. There is reasonable evidence that these conditions hold for mass-balance time series.
To estimate the standard deviation of any given geodetic balance, I propose to use the relation:
where σ 0 and dσ/dTw are parameters to be estimated. Equation (2) specifies a linear dependence of interannual variability on the temperature T w at the glacier’s equilibrium-line altitude (ELA) during the warmest month of the balance year. This choice is the outcome of an extensive exploration of the direct-balance data for possible influences on interannual variability, σd . For example σd is uncorrelated with the mass balance itself and with record length, although the spread of observed values is greater the shorter the record. There is a weak inverse correlation with glacier size, and the horizontal separation between measured glaciers is not a good predictor of σd (Fig. 4a).

Fig. 4. Possible determinants of interannual variability of mass balance. (a) Predictability of standard deviation from pairs of direct-balance standard deviations separated by distance s (km). See text for details of se σ (s). (b) σd for series of D longer than 12 years (selected to avoid unreliable short-record σd ) as a function of T w, the free-air temperature at the ELA during the warmest month (see text for details). Best-fit line, σd = 465 + 55 T w, derived by regression against single-glacier observations. Diamonds: class averages (class width 1°C).
Figure 4a is based on the standard error ![]() of pairs of standard deviations calculated for all glacier pairs (A,B). The se
σ
are sorted by s (the distance between A and B) and grouped into successive sets, along the s axis, of 40 measurement pairs each. The grey envelope, representing ± twice the standard error of each of these sets, shows that se
σ
increases very slowly with separation. Thus nearby glaciers with reliably known σd
offer no particular advantage over distant ones for estimating σg
.
of pairs of standard deviations calculated for all glacier pairs (A,B). The se
σ
are sorted by s (the distance between A and B) and grouped into successive sets, along the s axis, of 40 measurement pairs each. The grey envelope, representing ± twice the standard error of each of these sets, shows that se
σ
increases very slowly with separation. Thus nearby glaciers with reliably known σd
offer no particular advantage over distant ones for estimating σg
.
In Figure 4b, however, the variability depends recognizably on the continentality, glaciers with colder ELAs being more ‘continental’. The best-fit line (Equation (2)) explains 29% of the sample variance. The data are scattered, but the relationship is well defined enough to require that it be allowed for. Accordingly, I adopt Equatin (2) as the source of information for estimating σg .
This is consistent with Reference Braithwaite and ZhangBraithwaite and Zhang (1999), who showed that the interannual variability of mass balance scales with the balance amplitude (one-half of the difference between winter balance and summer balance). However, seasonal balances are even less widely measured than annual balances, and here a universally available measure of variability is needed. As noted by Reference BraithwaiteBraithwaite 2008; (see also Reference Ohmura, Sparling and HawkesworthOhmura and others, 1992), for any given annual balance a greater amplitude implies both snowier winters and warmer summers.
The quantity T w is interpolated to each glacier’s ELA from the US National Centers for Environmental Prediction–US National Center for Atmospheric Research (NCEP–NCAR) reanalysis (Reference KalnayKalnay and others, 1996) and an unpublished dataset of average ELAs at 1°×1° resolution. The reanalysis temperatures are climatological averages for 1968–96. The ELA data come principally from an enlarged version of the World Glacier Inventory (WGI) containing 125 000 glaciers (Cogley, 2008). The ELA is estimated by averaging the mid-altitudes (averages of minimum and maximum elevations; Reference Cogley and M.S.Cogley and McIntyre, 2003) of single glaciers. Where the WGI is incomplete, ELAs are estimated from surrogates. For example, much of the information for western North America consists of glaciation levels (e.g. Reference Ohmura, Kasser and FunkØstrem, 1972), reduced by 200 m following Reference Cogley and M.S.Cogley and McIntyre (2003).
Following Reference CogleyCogley 2004, (section 4.3), the difference due to unsampled natural variability between an n-year G and any one of the annual measurements g of which we imagine it to be composed is expected to be zero, with an uncertainty given by
This, however, is not a complete description of the uncertainty in g. The measured G is itself uncertain, and we must allot some of the measurement error to each of the n years in the span of the measurement. I assume that the measurement error seG is composed of equal annual contributions, so that the uncertainty in g due to measurement error is
Further, I assume that seNV and seME are independent. Combining Equations (3) and (4), this leads to
as our best estimate of the total uncertainty in each annual g.
Joint Analysis With Direct And Geodetic Measurements
We can now combine ‘measurements’ of annual g with measurements of annual d. Here I calculate global average B in the same way as in earlier work (Reference Cogley and AdamsCogley, 2005; Reference Kaser, Cogley, Dyurgerov, Meier and OhmuraKaser and others, 2006). The annual estimates are used to interpolate pentadal averages at each glacierized cell of a 1°×1° grid, these averages then being weighted by the glacierized area of the cell. When both d and g are available for any glacier, d is chosen and not g. When a set of up to five measurements is a mixture of ds and gs, its uncertainty is calculated as the standard deviation of the sample divided by the square root of m, the number of annual measurements. But when only gs are available the uncertainty is Σ(segi )/m.
Fig. 5 shows the new pentadal averages B in the context of recent estimates that used only direct measurements D. In all but the most recent pentads, B is more negative than the uncorrected arithmetic average of direct measurements, and in all but the 1956–60 pentads it is more negative than D.

Fig. 5. Pentadal calculations of global average mass balance, updating parts of figure 2 of Reference Kaser, Cogley, Dyurgerov, Meier and OhmuraKaser and others (2006). Triangles: arithmetic averages of direct balance measurements (C05a of Reference Kaser, Cogley, Dyurgerov, Meier and OhmuraKaser and others (2006), extended by completion of 2001–05 pentad. Circles: similarly extended averages with spatial interpolation from direct balance measurements to correct for spatial bias (equivalent to C05〉 of Kaser and others). Squares: averages with spatial interpolation from the combined direct and geodetic balance dataset introduced in this study, with grey confidence region representing ±2 standard errors about the mean.
First, however, note that D itself is now more negative than in Reference Kaser, Cogley, Dyurgerov, Meier and OhmuraKaser and others (2006). Their C05〉 was –481±50 kgm–2 a–1 for 2001–04, to be compared with the current D = –720±58 kgm–2 a–1. This is mainly because of newly assimilated measurements of d for 2005, which was a year of serious mass loss on a global average. As Figure 5 suggests, 2006 was probably even more negative, so incoming data provide no sign that the trend to faster mass loss is abating. The trend since 1971–75 is virtually unchanged (–10.5 kgm–2 a–2) in the transition from the D-only dataset to the D-plus-G dataset.
In 2001–05 B, at –740±62 kgm–2 a–2, is indistinguishable from D. This could be because, as yet, there are fewer recent geodetic measurements. More generally, it is not an accurate description of the past 50 years as a whole, and it is probably no longer correct to say that B was near to zero in the 1960s and early 1970s.
The small-glacier contribution to sea-level rise is now estimated at 1.12±0.14mma–1 SLE (sea-level equivalent) for 2001–05, as against the 0.77±0.15 mma–1 SLE of Reference Kaser, Cogley, Dyurgerov, Meier and OhmuraKaser and others (2006). These numbers exclude glaciers in Greenland and Antarctica. Kaser and others estimated 0.98 ±0.19 mma–1 SLE including those glaciers, and taking their approach to upscaling, the equivalent figure for the present study is 1.41 ±0.20mma–1 SLE.
Concluding Remarks
It seems probable that the global balances presented here are more negative than earlier estimates because of better representation of tidewater glaciers. This suggestion should be explored more thoroughly, as should the question of whether the enlarged dataset does in fact represent adequately the global-average ablation by calving. Note also that no progress has been reported here on the other biases discussed by Reference Kaser, Cogley, Dyurgerov, Meier and OhmuraKaser and others (2006).
The confidence region shown for B in Figure 5, derived from standard errors of polynomial coefficients estimated during spatial interpolation, is narrower than that of the consensus estimates presented by Reference Kaser, Cogley, Dyurgerov, Meier and OhmuraKaser and others (2006). If one of the purposes of spatial interpolation is to smooth away errors in the observations, then Figure 5 contains meaningful short-term detail that deserves investigation. The relative minimum in 1975–80 is an example. If, however, the errors of the polynomial coefficients are physically uninformative, an alternative method of estimating uncertainty must be found. Routine cross-validation calculations, in which an estimate of the balance is interpolated at each measured glacier but without the information from that glacier itself, typically yield root-mean-square differences (measured minus fitted) an order of magnitude greater than the errors in Figure 5. This would be much more cautious, but might require us to doubt whether global average mass balance is growing more negative.
Another note of caution should be sounded in conclusion. The error model for G is quite detailed, whereas the error model for D, unaltered in the present study, must now be seen as underdeveloped. As it stands, the error analysis favours measurements of d, because larger errors are usually assigned to g and the direct data tend to outweigh the geodetic data during averaging. However, the relative error weighting of the two kinds of data could be tuned plausibly within quite broad limits. The crude error model for d needs to be revisited, and the error model for G needs to be placed on a more secure observational footing, which will require better modelling of the interannual variability of mass balance. A considerable amount of work is necessary before the new dataset can be regarded as a source of homogeneous information, but it is likely that our estimates of the global average mass balance of small glaciers are now better.
Acknowledgements
I thank all those colleagues who have published measurements of mass balance, whether by geodetic or direct methods, and the World Glacier Monitoring Service, Zürich.








