Introduction
The flow behaviour of ice is influenced by a preferred orientation of the anisotropic ice crystals (Reference AlleyAlley, 1992). With the existing stresses in the ice sheet or glacier, the ice crystals orient away from the tension axis (e.g. Reference Gow and WilliamsonGow and Williamson, 1976). This developed anisotropic fabric influences the viscosity, and thus flow behaviour, of the ice, as shear strength can be several orders of magnitude less parallel to the basal plane of an ice crystal than perpendicular to it (Reference Ashby and DuvalAshby and Duval, 1985; Reference Cuffey and PatersonCuffey and Paterson, 2010).
The knowledge of the distribution of the crystal-orientation fabric (COF) is mainly provided from deep ice cores from Antarctica and Greenland, optimized for palaeoclimate record reconstructions, typically located at ice domes, divides (or very shallow flanks) with special flow regimes (e.g. Reference Thorsteinsson, Kipfstuhl and KipfstuhlThorsteinsson and others, 1997; Reference DiPrinzio, Wilen, Alley, Fitzpatrick, Spencer and GowDiPrinzio and others, 2005; Reference MontagnatMontagnat and others, 2012; Reference Faria, Weikusat and WeikusatFaria and others, 2013). However, this is only local information for these special stress regimes. Thus, a method is needed that derives information about the distribution of COF with depth over larger areas on glaciers and ice sheets. Some studies exist where radar methods are used to investigate the COF distribution on a local scale (Reference Fujita, Maeno and MaenoFujita and others, 2006; Reference Eisen, Hamann, Kipfstuhl, Steinhage and SteinhageEisen and others, 2007; Reference Matsuoka, Wilen, Hurley and RaymondMatsuoka and others, 2009) as well as over larger areas (Reference MatsuokaMatsuoka and others, 2003). Here reflection signatures from changing COF need to be distinguished from reflections due to acidity contrast or density; this is possible using multi-frequency and multi-polarization analysis (Reference Eisen, Hamann, Kipfstuhl, Steinhage and SteinhageEisen and others, 2007; Reference Drews, Eisen, Steinhage, Weikusat, Kipfstuhl and KipfstuhlDrews and others, 2012; Reference Matsuoka, Power, Fujita and RaymondMatsuoka and others, 2012). However, high frequencies are needed to see COF-induced reflections, which limits the penetration depth of the radar waves (Reference Fujita, Maeno and MaenoFujita and others, 2006).
In addition to radar waves, the propagation of seismic waves is influenced by developed anisotropic ice fabric (Reference Robertson, Bentley, Bentley and HayesRobertson and Bentley, 1990). Additionally, seismic wave propagation in cold ice depends mainly on density (Reference KohnenKohnen, 1972) and temperature distributions (Reference KohnenKohnen, 1974; Reference Gammon, Kiefte, Clouter and DennerGammon and others, 1983). The most extensive study of the influence of anisotropy on seismic wave propagation and the calculation of seismic velocities for different cone fabrics is that of Reference BennettBennett (1968); this was applied to seismic measurements from Dome C, Antarctica, by Reference Blankenship and BentleyBlankenship and Bentley (1987). They pointed to the importance of the crystalline fabric for modelling ice-sheet dynamics and the potential of seismic measurements to obtain information about the anisotropy.
In most seismic studies the ice is assumed to be isotropic (e.g. when analysing reflection amplitudes to characterize the ice/bed interface). Englacial seismic reflections were observed in seismic surveys from Antarctica (Reference HorganHorgan and others, 2012; Reference HofstedeHofstede and others, 2013) and Greenland (Reference HorganHorgan and others, 2008), and have been interpreted as arising from abrupt changes in the orientation of the ice-crystal fabric. The analysis of ultrasonic sounding measurements (Reference BentleyBentley, 1972) to derive information about the existing anisotropy is easier, as there are fewer ambiguities in the datasets than those of seismic reflection surveys. Reference Gusmeroli, Pettit, Kennedy and RitzGusmeroli and others (2012) connected the largest eigenvalue describing COF with P-wave velocities from ultrasonic sounding at Dome C. However, ultrasonic sounding uses frequencies in the kHz to MHz range and requires a borehole or ice core. Recently, the anisotropic fabric has been investigated by analysing the dispersion curves of surface waves (personal communication from S. Picotti, 2013).
In 2010 a seismic survey was carried out on Colle Gnifetti, on the Swiss/Italian border in the Alps, to test the overall approach of using a lightweight micro-vibrator on snow. This micro-vibrator excited P-waves (compressional waves), as well as SH-waves (horizontal shear waves), and proved to be an efficient source in conditions such as those found at Colle Gnifetti. When the data were processed and the stacked sections were later converted to depth, the ice thickness derived from the P-wave basal reflection did not match that observed in the nearby KCI ice core. In contrast, the depth of the bed reflection of the SHwave sections fitted well. This depth discrepancy and the large difference in accuracy between P- and SH-wave depth conversion could not, at first, be explained (Reference Polom, Hofstede, Diez and DiezPolom and others, 2013).
In this paper we show the large influence of the developed anisotropic ice fabric on short-spread (offset/ depth ≤ 1) seismic reflection P- and SH-wave data under the assumption of isotropy used for standard processing. We calculate anisotropic P- and SH-wave velocities taking density, temperature and COF distribution from the KCI ice core on Colle Gnifetti into account. For the calculation of P-wave velocities in the firn pack we use the empirical formula of Reference KohnenKohnen (1972). To enable us to also consider the influence of density on SH-wave velocities, we derive a new relationship between S-wave velocity and density from the diving waves. We will refer to ‘S-waves’ in the context of this density/S-wave velocity relationship, as no anisotropy is taken into account, and to ‘SH-waves’ for the analysis of the anisotropy. By comparing anisotropic normal moveout (NMO) velocities with zero-offset velocities we find an explanation for the difference in depth between the depth-converted P-wave section and the SH-wave section, that is less influenced by the anisotropy. Thus, we show that the error introduced by assuming isotropy and deriving depth-conversion velocities from stacking velocities is no longer negligible in the case of P-wave data from an anisotropic ice fabric. However, this systematic difference yields the possibility of deriving information about the anisotropic fabric by combining seismic P-wave data with other datasets (e.g. radar data, borehole data or SH-wave data).
First, we describe the theory of NMO velocities in anisotropic media and explain the influence of anisotropy, using the example of a single layer where all ice crystals are oriented vertically. Then we introduce our seismic data from Colle Gnifetti and compare the stacking velocities of these seismic datasets to anisotropic NMO velocities calculated from the KCI ice core. Finally, we combine the seismic data with radar data from Colle Gnifetti to derive information about the anisotropy directly from the combination of these two datasets.
Normal Moveout (NMO)
To determine the depth of observed reflection horizons from seismic data a reliable velocity model is needed. This velocity model is normally generated by fitting a hyperbola to the observed reflections. Here the travel times increase due to the increasing offset caused by the shot-receiver geometry. Thus, the stacking velocities are obtained. In the isotropic case and for short-spread (offset/depth ≤ 1) seismic reflection data, these stacking velocities, or NMO velocities, can be considered as root-mean-square (rms) velocities. Hence, they are used to calculate interval velocities (depth-conversion velocities) for the different layers and used to determine depth from two-way travel time (TWT).
In case of seismic wave propagation in anisotropic media, which is present when ice crystals show a preferred orientation, the wavefronts are no longer spherical. Thus, the travel times for different incoming angles do not only depend on the longer travel paths due to increasing offsets, but are also influenced by the angle dependency of the velocities. Seismic velocities for cone fabrics in ice can be calculated with the well-known equations (see Appendix) derived by Reference BennettBennett (1968). These cone fabrics (Fig. 1, inset), where all ice crystal c-axes are oriented within the enveloping of a vertically oriented cone, correspond to vertical transversely isotropic (VTI) media.
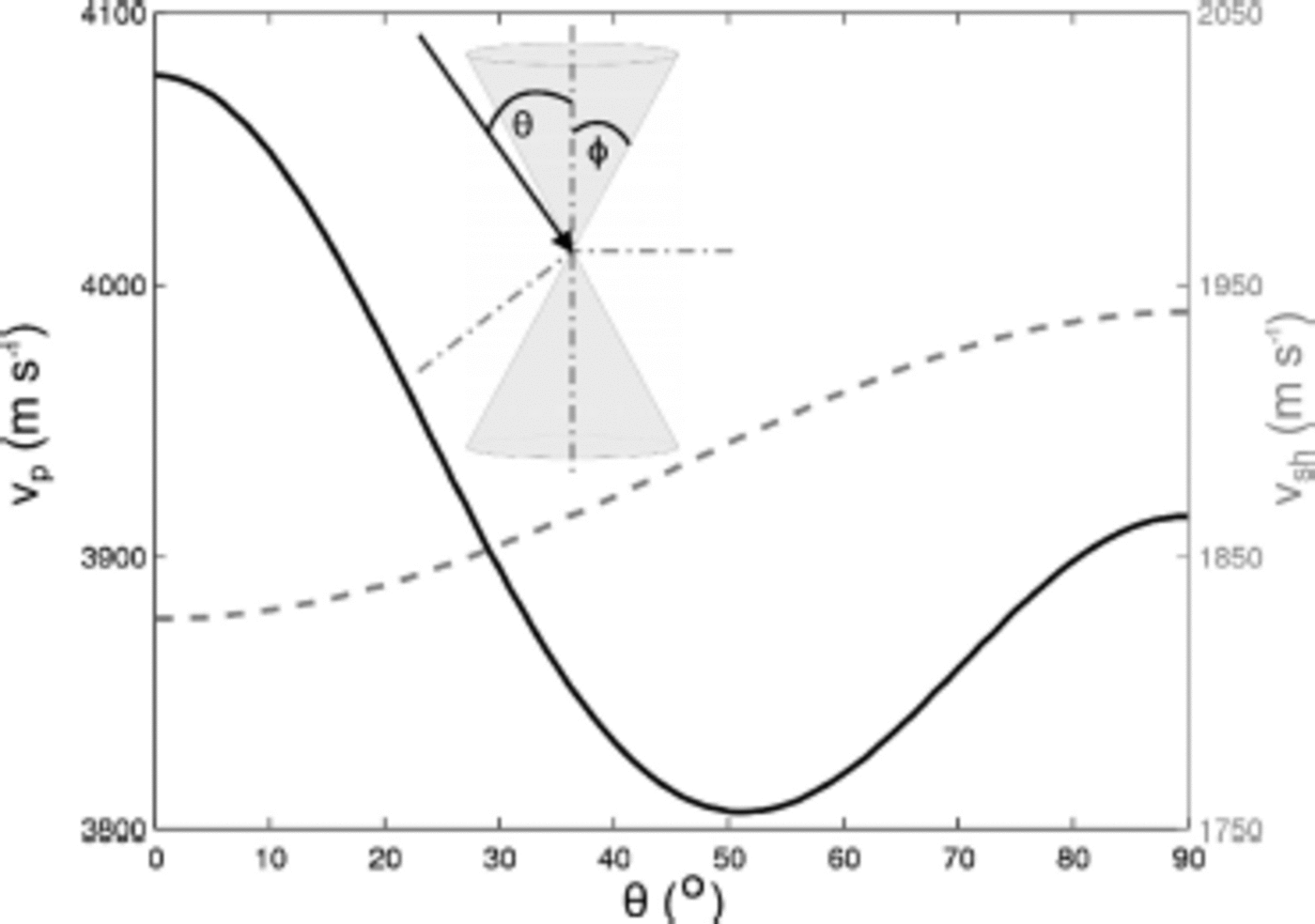
Fig. 1. The enveloping (apex) of ice crystal c-axes distribution for a vertically oriented cone fabric with opening angle Ф . The angle of the seismic ray (solid arrow) to the vertical is given by 0 . P- (dark curve) and SH-wave (dashed grey curve) velocities for a vertical single-maximum fabric (cone angle Ф = 0°) for incident angles, θ, between 0° (vertical) and 90° (horizontal), calculated from the equations given by Reference BennettBennett (1968) (Eqns (A1) and (A2)).
Using the Reference BennettBennett (1968) equations the P- and SH-wave velocities (v p(θ) and v sh(θ), respectively) for different angles of incidence, 0 (with respect to the vertical), are calculated using the opening angle, ф, of this solid cone (Fig. 1, inset). Figure 1 shows the synthetic P- and SH-wave velocities for an ideal vertical single-maximum (VSM) fabric, where all ice crystal c-axes are oriented vertically (cone angle Ф= 0°). This is the most extreme form of anisotropy we can expect in ice. The SH-wave velocity is slowest parallel to the c-axis of the ice crystal and increases by 6% for waves travelling perpendicular to the c-axis. The P-wave velocity is highest parallel to the c-axis of the ice crystal and 4% lower perpendicular to it. However, the lowest P-wave velocity is at 0 = 52° incoming angle, with a velocity ~ 7% lower than the vertical velocity.
In the anisotropic case it is no longer valid to determine the depth-conversion velocities from stacking velocities. The NMO velocities, for single as well as multiple layers, can be approximated using the Thomsen parameters (Thomsen, 1986). Usually the Thomsen parameters are given as dependent on the components of the elasticity tensor. In the case of weak anisotropy they can also be described by the vertical (v p(0°), v sh(0°)), horizontal (v p(90°), v sh(90°)) and 45° (v p(45°)) velocities. The near-vertical dependency of the P-wave velocity, v p(θ), is determined by the Thomsen parameter
while the SH-wave velocity can be described by the Thomsen parameter
The stacking velocity for anisotropic material of short-spread seismic data can then be approximated using the anisotropic NMO velocity (Thomsen, 1986):
with ζ being either the P- or SH-wave velocity and ξ the corresponding Thomsen parameter, δ or ϒ, respectively. Thus, the anisotropic NMO velocity is a combination of the zero-offset velocity (v p(0°) or v sh(0°)) and the corresponding Thomsen parameter that includes information about the anisotropy. For interval velocities we use lower-case letters, hence, the anisotropic, angle-dependent velocity given by Reference BennettBennett (1968) is denoted vζ(θ) (Eqns (A1) and (A2)), the zero-offset velocity is v ζ(0°) (Eqns (A1) and (A2), θ = 0°) and the anisotropic NMO velocity is v nmo ζ (Eqn (3)).
For isotropic, as well as anisotropic, conditions, the stacking velocities determined from the seismic data are used to carry out the NMO correction to align the common-midpoint sorted data for stacking. For the conversion of TWT to depth in the isotropic case the picked stacking velocity can be used to determine directly the depth-conversion velocity. In the anisotropic case the stacking velocity is now identified as the anisotropic NMO velocity, vnmo c. For depth conversion in the anisotropic case we must use, the velocity for the zero-offset case, v p(0°) or v sh(0°). However, this zero-offset velocity cannot be derived from the seismic data alone and is, thus, normally unknown. An error is introduced in the depth conversion if the existing anisotropy is not considered, and the stacking velocity is used to determine the depth-conversion velocity, this means that the anisotropic NMO velocity, vnmo ζ (Eqn (3)), is used for the depth conversion instead of the zero-offset velocity, v ζ (0°).
In most seismic studies we do not deal with one layer but with a multilayer case. Similar to the calculation of rms velocities, VRMS , in the isotropic case, by summing over squared interval velocities, the anisotropic NMO velocity for a multilayer case can be calculated as the rms velocity of the anisotropic, single-layer NMO velocities (Reference Alkhalifah and AlkhalifahAlkhalifah and Tsvankin, 1995; Reference TsvankinTsvankin, 2001)
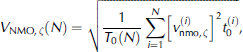
with the zero-offset TWT for the single layers t0
(i)
for N layers and ![]() . For rms velocities we use upper-case letters, hence denoting the zero-offset rms velocities as V
RMSζ(0-), the anisotropic NMO velocities as V
NMO c (Eqn (4)) and the stacking velocities picked from our seismic datasets from Colle Gnifetti as V
EIViS,ζ.
. For rms velocities we use upper-case letters, hence denoting the zero-offset rms velocities as V
RMSζ(0-), the anisotropic NMO velocities as V
NMO c (Eqn (4)) and the stacking velocities picked from our seismic datasets from Colle Gnifetti as V
EIViS,ζ.
Example: single layer
To illustrate the influence of anisotropy on P- and SH-wave moveout, A t (arrows, Fig. 2), in ice, we investigate a single, 50 m thick layer of VSM fabric. We calculate angle-dependent P- and SH-wave velocities, vζ(0) (Eqns (A1) and (A2)), for an offset/depth-range≤ 1, as well as zero-offset velocities, v ζ(0°) (Eqns (A1) and (A2)), and anisotropic interval NMO velocities, vnmo ζ (Eqn (3)).
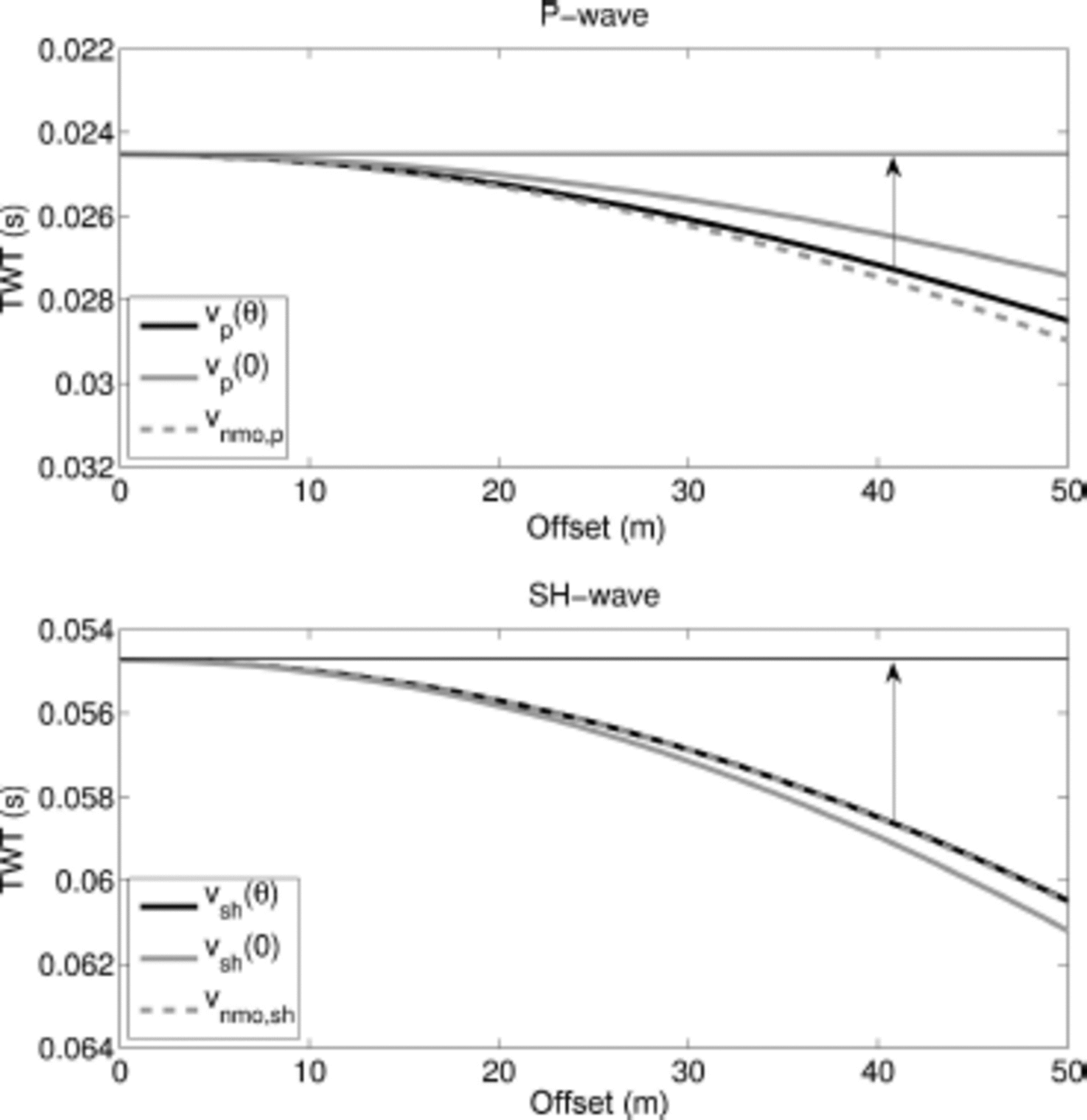
Fig. 2. Example of offset-dependent travel times for a single layer, 50 m thick, with a vertical single-maximum fabric. The moveout time, At, that needs to be corrected is indicated by black arrows. The thick black lines show the TWT calculated from the velocities of Figure 1. The TWT calculated from the NMO velocity, v nmo ζ, derived using the Thomsen parameters, δ and γ, is given by the dashed grey curves. The TWT for the corresponding zero-offset velocities, v ζ(0°), is given by the solid grey curves. The zero-offset and NMO velocities are constants for each layer and wave type. The difference between v nmo,ζ and v ζ(0°) is 20% for the P-wave and 6% for the SH-wave.
The thick black curves in Figure 2 show the travel times calculated from the corresponding angle-dependent P- and SH-wave velocities, vζ(0) (Fig. 1), that were calculated using the equations of Reference BennettBennett (1968). Hence, those are the travel times we would measure with a seismic survey for this single, 50 m layer of VSM fabric. The corresponding anisotropic interval NMO velocities, v nmo ζ (Eqn (3)), for this example are 3240 ms"1 for the P-wave and 1937 ms"1 for the SH-wave. As the elasticity tensor for a single crystal is given by Reference BennettBennett (1968), here we use the more exact calculation of the Thomsen parameters by means of the elasticity tensor. The travel times calculated from these anisotropic NMO velocities are shown as the dashed grey curves in Figure 2. For the SH-wave, they approximate the travel times calculated by means of the Reference BennettBennett (1968) equations (vc(θ), thick black curve in Fig. 2) very well. For the P-wave an increasing difference between the travel times calculated with the Reference BennettBennett (1968) equations (v p(θ), thick black curve) and the travel times calculated from the anisotropic NMO velocity (v nmo p, dashed grey curve) can be observed. The larger difference for the fit in the case of the P-wave, compared to that of the SH-wave, between TWT from anisotropic interval NMO velocity (v nmo ζ dashed grey curve) and TWT from angle-dependent velocity (vζ(θ), thick black curve) is caused by the fact that the P-wave velocity, v p(<θ), has a minimum for the velocity at the incoming angle of 52° (Fig. 1). The Thomsen parameter, 8, however, describes the near-vertical dependency of the P-wave. This means, that for increasing offset and, thus, larger incoming angles, the velocity cannot be approximated accurately with the Thomsen parameter, δ, alone.
When a velocity analysis is carried out we determine the stacking velocity by fitting a hyperbola to the measured travel times (solid black curves in Fig. 2) and then identify this velocity as the anisotropic NMO velocity, vnmo ζ (dashed grey curves). For the depth conversion we now need the zero-offset velocity, which we do not know from the stacking velocity. For the 50 m VSM layer example the zero-offset velocity, v ζ(0°), is 4077 and 1827 ms"1 for the P- and SH-wave, respectively. The travel times over offset for these velocities are shown as the solid grey curves in Figure 2.
The difference between the anisotropic interval NMO velocity, v nmo ζ, and the zero-offset velocity, v ζ(0°), for this example is 20% in the case of the P-wave but only 6% in the case of the SH-wave. Thus, in both cases, but especially in the case of the P-wave, a large error is introduced by assuming isotropy during the processing and using stacking velocities to directly derive the depth-conversion velocities.
Data and Field Site, Colle Gnifetti
Colle Gnifetti is a glacier saddle in the Monte Rosa region, situated on the Swiss/Italian border at 4500 m a.s.l. (Fig. 3). It has been studied intensively during recent decades. Falling into the recrystallization-infiltration zone (Reference ShumskiyShumskiy 1964) it is an excellent and accessible field site, used to test new methods and techniques for investigations in polar regions and for the study of European climate records. Only some thin melt layers and ice lenses can be found (Reference Eisen, Nixdorf, Keck and KeckEisen and others, 2003). The overall net snow accumulation at Colle Gnifetti is quite low, with strong variations between 15 and 50cm w.e.a-1, caused by strong wind erosion (Reference Alean, Haeberli and SchädlerAlean and others, 1983). The KCI ice core was drilled on Colle Gnifetti in 2005, in an area of especially low accumulation (Reference BohleberBohleber, 2011). Besides the study of the glaciological features of Colle Gnifetti (Reference Haeberli and HaeberliHaeberli and Alean, 1985; Reference SchwerzmannSchwerzmann, 2006), ice thickness and stratigraphy were investigated using ground-penetrating radar (GPR) methods (Reference Haeberli, Schmid and SchmidHaeberli and others, 1988; Reference WagnerWagner, 1996; Luthi, 2000; Reference Eisen, Nixdorf, Keck and KeckEisen and others, 2003; Reference Konrad, Bohleber, Wagenbach, Vincent and VincentKonrad and others, 2013).
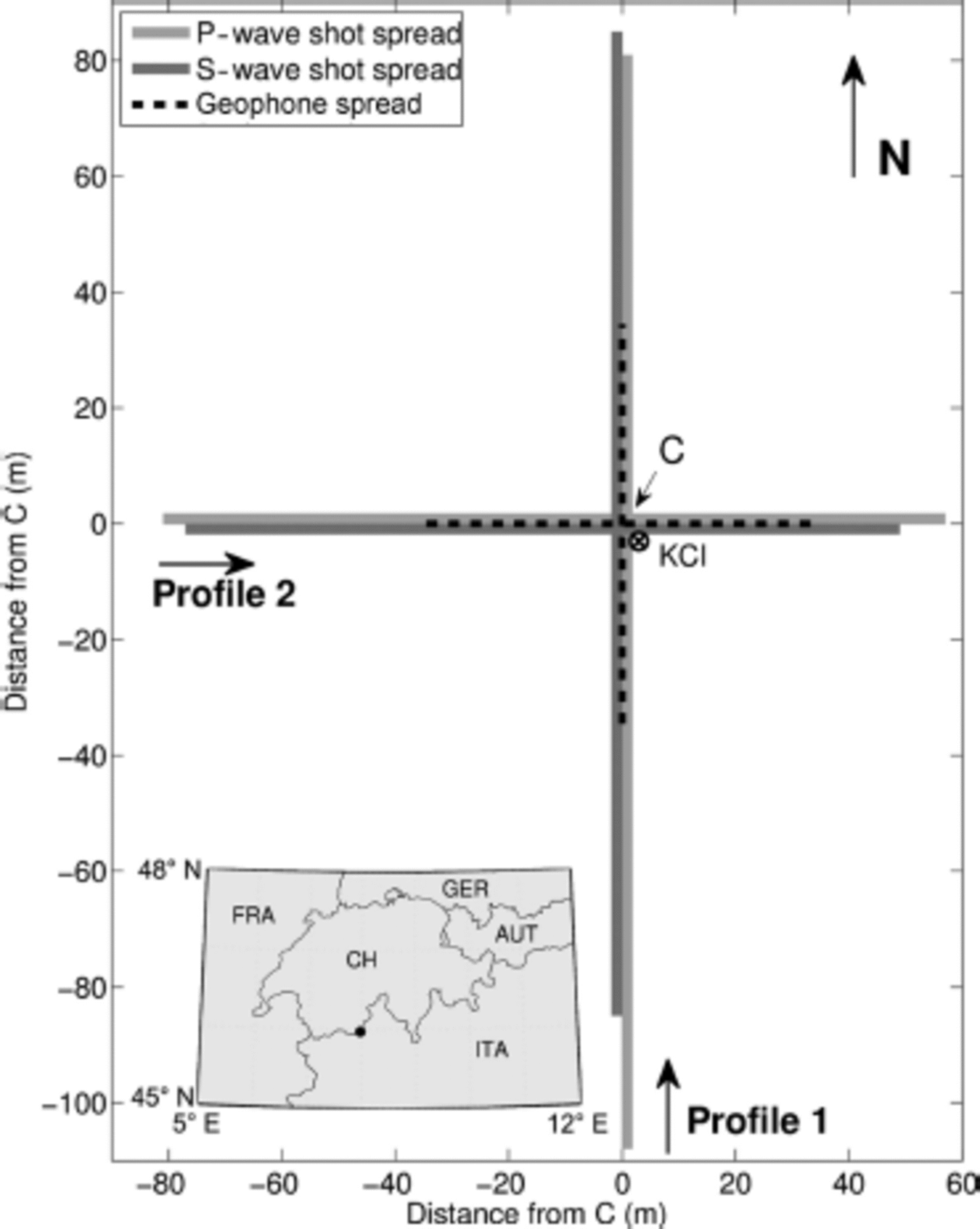
Fig. 3. Geometry of seismic survey. The light grey lines denote the shot spread of the P-wave survey, the dark grey lines the shot spread of the SH-wave survey. The dashed black lines show the geophone spread, geophones placed at 3 m intervals for the P-wave survey and 1.5 m intervals for the SH-wave survey. The lines cross at the centre point, C, close to the KCI ice core. The inset shows the location of Colle Gnifetti (black dot) on the Swiss/Italian border.
Ice-core and borehole data
The KCI ice core (45.929728 N, 7.876928 E, WGS84, measured in 2008) was drilled near the Swiss/Italian border to 62 m depth, close to the glacier bed. Drilling stopped when the first dirt intrusions occurred, so the bed is probably ~1 m deeper, as inferred from borehole radar data (Reference BohleberBohleber, 2011). Seismic surveys carried out in 2008 and 2010 were centred around the borehole location of the KCI ice core (Fig. 3). Thus, the ice-core measurements can be used for comparison with the seismic datasets (Fig. 4).
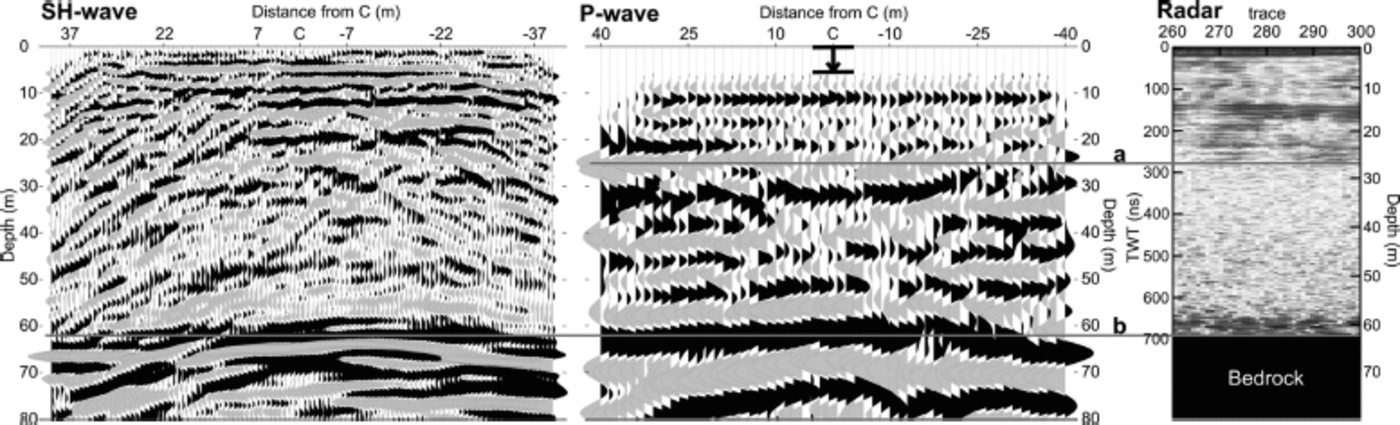
Fig. 4. Stacked data from the survey using the ElViS micro-vibrator as a source on profile 1 (north–south) in SH-wave and P-wave modes. Distances are shown from the centre point, C, close to the KCI ice core. The bed reflector can clearly be seen in both seismic datasets, just below 60 m depth (solid grey line), with coherent englacial reflections visible above. Additionally, some dipping reflectors are visible in the SH-wave data (Reference Polom, Hofstede, Diez and DiezPolom and others, 2013). The P-wave stack was shifted down for 6 m (marked with the black arrow). Far right panel: Forty traces (corresponding to 8 m) of a radar profile close to the KCI ice core. The grey line at 28 m shows the finishing of englacial reflection horizons and the seismic reflection in the P-wave data around the firn/ice transition used for calculating the anisotropy.
Density measurements (Reference Jahn(Jahn, 2006) on the ice core using 7-attenuation (Reference WilhelmsWilhelms, 1996) at sub-centimetre resolution (Fig. 5c, solid grey line) revealed some melt layers in the upper 15 m and the firn/ice transition zone at ~30 m depth. Temperatures measured at numerous borehole sites on the plateau were analysed by Reference Hoelzle, Darms, Lüthi and SuterHoelzle and others (2011), who found an increase in firn temperature since 1991, presently at ~0.168Ca-1. Temperature measurements in the KCI borehole in 2007 revealed temperatures of -11 to -138C. A strong negative temperature signal of -158C at 7 m depth was observed in 2008 (http://cryomap.cryosphere.ch,B05-1).
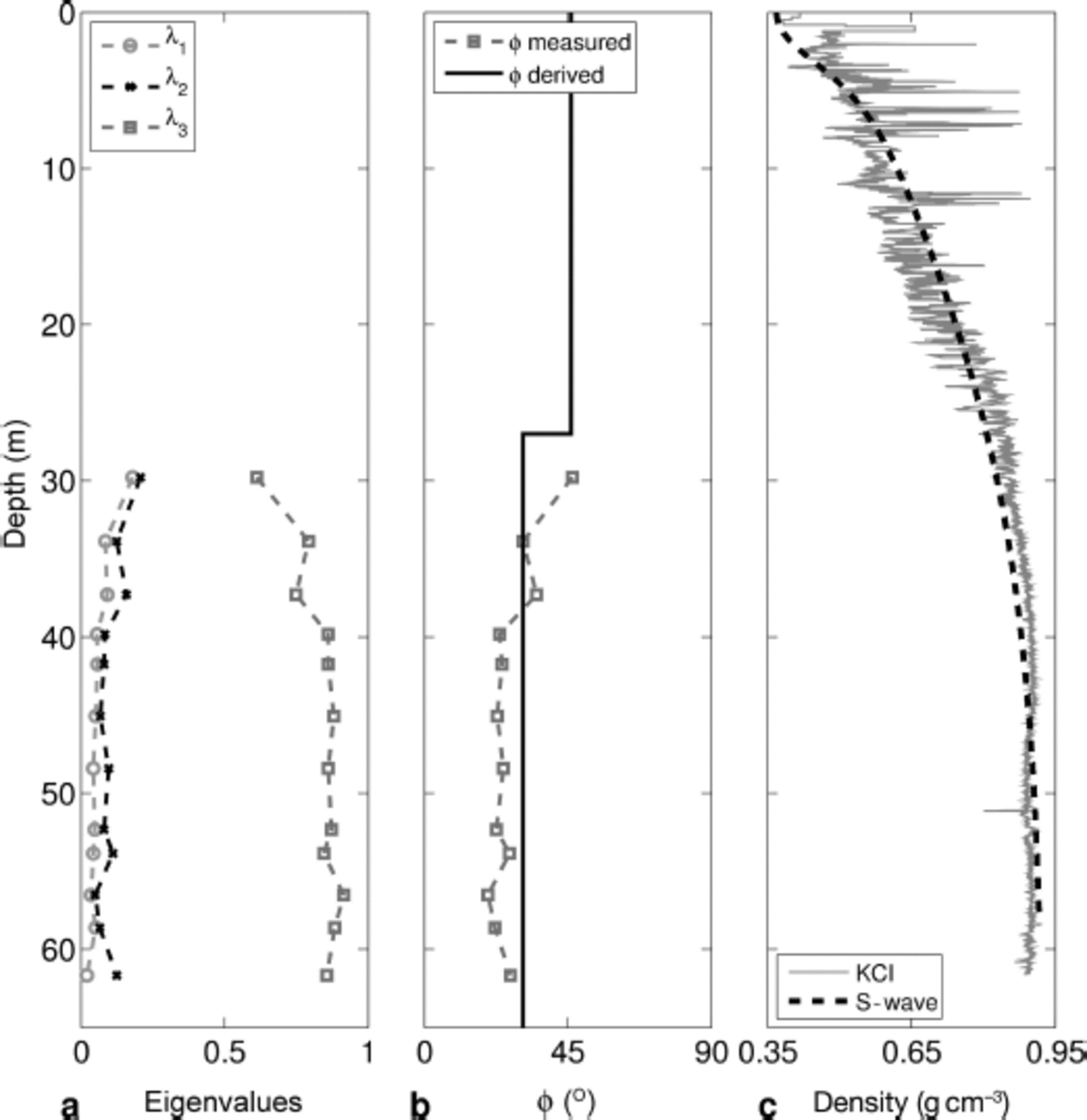
Fig. 5. Data measured along ice core KCI. (a) Eigenvalues of the second-order orientation tensor measured below 30 m depth with the corresponding angles of spherical aperture shown in (b), dashed curve. The black curve in (b) shows the cone opening angles, ф, derived from the δ values of the combined seismic/radar data analysis. The densities measured along the KCI ice core (grey curve) are displayed in (c), together with the best fit for the velocity profile derived from the S-diving waves (black curve) of profile 1 that was used to derive an S-wave/density relationship (Eqn (5)).
The KCI ice core was stored at -308C from 2005 on, and in 2012 the c-axis orientation fabrics were measured on the ice below the firn/ice transition zone at ~ 5 m intervals (12 samples were used for this study). Measurements have been carried out on thin sections (~(50 x 100 x 0.3) mm3), using the polarization microscopy method applying an automatic fabric analyser (e.g. Reference Wilson, Head and SimWilson and others, 2003; Reference Peternell, Hasalova, Wilson, Piazolo and PiazoloPeternell and others, 2010). The c-axis orientation distributions were analysed using the second-order orientation tensor. It can be described as analogous to the calculation of the inertia matrix of a system, where c-axes are represented through mass points on the surface of a unit sphere. The eigenvalue decomposition of the matrix defines the inertia ellipsoid with the eigenvalues (λ1 ≤ λ2 ≤ λ3 and ∑λ i = 1; Fig. 5a) being the principal axes lengths. The measured cross-sectional area of the crystallites is used as the statistical weight of the polycrystal (Reference Gagliardini, Durand and DurandGagliardini and others, 2004). This resembles the conditions for the seismic waves very well, as grain size is implicitly included in this information. In addition to the eigenvalues, the spherical aperture has been calculated, describing the opening angle of a cone centred on the average c-axis enveloping the distribution of c-axes (Fig. 1, inset and Fig. 5b, dashed grey line).
Seismic measurements
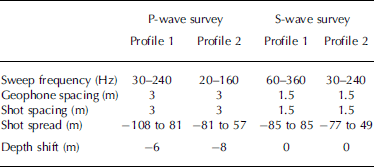
The seismic measurements used in this study were carried out on Colle Gnifetti in August 2010 (Polom and others 2013). We shot two profiles perpendicular to each other (Fig. 3) to allow us to evaluate variations in the anisotropy for different directions in space. As a source we used a lightweight micro-vibrator, ElViS (Electrodynamic-Vibrator System; Reference Druivenga, Grossmann, Grüneberg, Polom and PolomDruivenga and others, 2011), which we operated in both P-wave and SH-wave modes, on both profiles. The geometry settings for both profiles and both wave types are listed in Table 1 (Reference Diez, Eisen, Hofstede, Bohleber and BohleberDiez and others, 2013; Reference Polom, Hofstede, Diez and DiezPolom and others, 2013).
Table 1. Geometry for P- and SH-wave surveys of profiles 1 and 2
The raw data were correlated with the corresponding pilot sweep, and then amplitude scaling, bandpass filter and frequency-wavenumber (F-K) filters were applied. The data were then used to pick stacking velocities for the different wave types and profiles independently. These stacking velocities were used for the NMO correction and afterwards, in a smoothed form, to determine depth-conversion velocities to convert the TWT to depth (Reference Polom, Hofstede, Diez and DiezPolom and others, 2013).
Figure 4 shows the stacked seismic P- and SH-wave data of profile 1. The stacked data clearly show the bed reflection (grey line b) for the P-wave, as well as for the SH-wave data. The thickness of the glacier at our survey location, ~62(+1)m, is known from the length of the KCI ice core and borehole radar data. The depth of the bed reflection of the SH-wave data, after depth conversion, fitted this length. The depth of the bed reflection of the P-wave data was ~6 m (10%, profile 1) and 8 m (13%, profile 2) too shallow. Thus, the stacked P-wave data were shifted down, as indicated by the black arrow in Figure 4. Englacial reflections could be observed in both the SH-wave and P-wave stacks, such as the strong englacial reflection at ~28 m depth, that is used for the investigation of anisotropy below (Fig. 4, grey line a). The data processing and the observed reflections are discussed in detail by Reference Polom, Hofstede, Diez and DiezPolom and others (2013) and Reference Diez, Eisen, Hofstede, Bohleber and BohleberDiez and others (2013).
Until now, we have been unable to explain the depth mismatch in the case of the P-wave data at the same time as the good agreement of the SH-wave depth-converted data with ice-core and radar data. Possible reasons that might influence the velocity analysis (in addition to anisotropy) and might, thus, introduce an error in the depth estimate of the seismic data include effects of dipping reflectors, lateral inhomogeneities or the estimation of depth-conversion velocities from stacking velocities.
Deriving the depth-conversion velocities from stacking velocities is always associated with a certain error, even in the isotropic case (Reference Etris, Crabtree, Dewar and DewarEtris and others, 2001). However, these possible errors in the velocity analysis should affect the SH-wave velocity analysis as well as the P-wave velocity analysis and, thus, cannot explain why the depth estimate from the SH-wave is so good and the depth estimate from the P-wave is off by up to 13%.
Modeling Velocity Profiles from COF Data
To investigate the influence of anisotropy on the travel times at Colle Gnifetti and, thus, the effect of using stacking velocities to derive depth-conversion velocities in the anisotropic case, we use the ice-core data from KCI and forward model anisotropic velocities. Three datasets are important here for the calculation of velocities: the density, the temperature profile and the COF measurements in the form of the opening angle (Fig. 5).
The velocity calculation of Reference BennettBennett (1968) with the cone opening angle is based on measurements of the elasticity tensor at a temperature of -10°C. For the borehole of the KCI ice core, Reference Hoelzle, Darms, Lüthi and SuterHoelzle and others (2011) give temperatures between -11 and -13°C. As variations are only moderate over the whole depth, we correct the velocities for a temperature difference of -2°C for the complete depth. For the corrections we use gradients of -2.3 ms"1 K-1 for the P-wave and -1.2ms-1 K-1 for the S-wave, as given by Reference KohnenKohnen (1974).
At Colle Gnifetti a strong density gradient exists for the -30 m thick firn pack (Fig. 5c, grey line). To calculate the P-w wave velocity in firn we use the empirical formula given by Reference KohnenKohnen (1972) that gives a density/P-wave relationship. To simulate the velocities for the SH-wave a relationship between density and S-wave velocity is required. To derive such a new relation we picked the travel times of the diving waves of the ElViS profile 1 S-wave dataset. The travel time data from profile 2 were not used, as the picks showed large variations for travel times from different shots with the same offsets (10-15%). Using the Herglotz-Wiechert inversion (Reference KohnenKohnen, 1972; Reference King and JarvisKing and Jarvis, 2007; Reference Diez, Eisen, Hofstede, Bohleber and BohleberDiez and others, 2013) we derive the velocity, vs , and corresponding depth, z, at the turning point of the diving waves. This S-wave velocity profile, together with the KCI densities, can then be used to derive a relationship between density and S-wave velocity at depth z:
with the density of ice, pice (kg m-3), and the S-wave velocity of ice, v s,ice (ms-1). The dashed black line in Figure 5c shows the densities calculated from the S-wave velocity profile, derived from the diving waves of profile 1, using Eqn (5). The rms deviation of these densities to a moving average (mean over 0.5 m intervals) of the KCI densities (Fig. 5c, grey line) is ±25 kgm-3. Hence, we are not only able to correct the P-wave but also the SH-wave velocities for the strong density gradient in the firn column.
We use the opening angles of the cone fabric derived from the KCI ice-core data (Fig. 5b, dashed grey line) and calculate velocities using the equations given by Reference BennettBennett (1968). Corrections for density and temperature are made on these velocities. Between 0 and 30 m depth, where no COF measurements were carried out, the firn is assumed to be isotropic. From the derived velocities we then calculate the Thomsen parameters, δ and γ (Eqns (1) and (2)). Thus, we derive interval values for the P- and SH-wave anisotropic NMO velocities, v nmo,ζ (Eqn (3)), and zero-offset velocities, v ζ(0°), that can then be used to derive the corresponding rms velocities. The rms velocities, V NMO ζ, (dashed black curves) and V RMS,ζ(0°) (solid grey curves), together with the picked velocities of the ElViS datasets, V ElViS,ζ (solid black curves), are shown in Figure 6 for the P- and SH-waves.
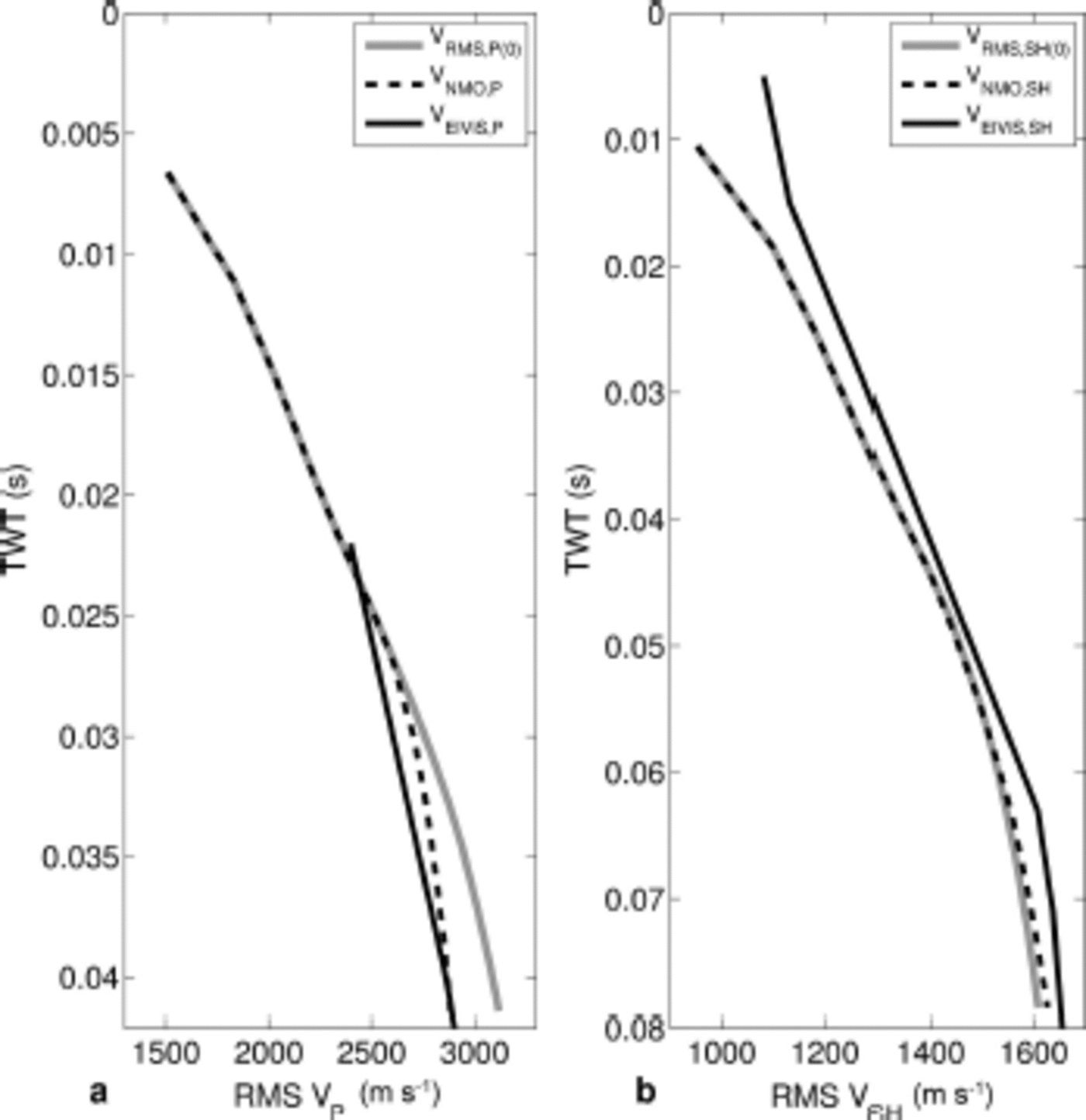
Fig. 6. Picked and calculated (a) P- and (b) SH-wave rms velocities for comparison of the influence of anisotropy on the seismic velocities. The solid black curves show the velocities V ElVis, ζ picked from the NMO analysis of the ElViS datasets (profile 1). Using the KCI measurements of density, temperature and COF, we calculated the NMO velocities, V NMO, ζ (dashed black curves), and zero-offset rms velocities, V RMS, ζ(0°) (grey curves).
In the case of the P-wave, the velocities picked from the ElViS P-wave data are within 2% of the anisotropic NMO velocities, V NMO,P, derived from the KCI ice-core data. The velocity needed for the depth conversion is, again, the zero-offset velocity, V RMS,P(0˚). This P-wave zero-offset velocity (3119ms-1) is 228ms-1, i.e. 7%, higher than the anisotropic P-wave NMO velocity (2891 ms"1) for the bed reflection. For the SH-waves the calculated anisotropic NMO velocities, VNMO, SH, and zero-offset rms velocities, V RMS,SH(0°), are shifted compared to the picked values. This is probably due to the correction of the velocities for the density (Eqn (5)). The significant aspect here is, however, that the difference between zero-offset (1610 ms"1) and anisotropic NMO velocities (1628 m s"1) is only 18 ms-1, i.e. 1%.
We now compare the zero-offset rms velocities, VRMS ζ(0°), with the anisotropic NMO velocities, V NMO,ζ, for the multilayer case at Colle Gnifetti, calculated using density, temperature and COF measurements from the KCI ice core. The difference between anisotropic NMO velocity, V NMO, ζ, and zero-offset rms velocity, V RMS,ζ(0) is determined by the Thomsen parameters, δ and γ. The results show a large difference in the developed anisotropy on P- and SH-wave velocity analysis, when assuming an isotropic state and using stacking velocities (i.e. anisotropic NMO velocities) to determine the depth-conversion velocities. The influence of the anisotropy on the depth conversion of the SH-wave section is not significant (1%), whereas the influence is not negligible for the P-wave stack (7%). Hence, it is possible to explain why the conventional depth conversion, based on stacking velocities, worked well for the SH-wave at Colle Gnifetti but caused a considerable mismatch in the case of the P-wave.
Deriving δ as a Proxy for Anisotropy
The difference between the zero-offset velocity and the anisotropic NMO velocity for the P-wave at Colle Gnifetti shows the sensitivity of the P-wave moveout, At, to the existing anisotropic fabric. This sensitivity enables us to derive information about the anisotropy from the analysis of P-wave data. However, the small difference, only 1%, between the zero-offset velocity and the anisotropic NMO velocity for the SH-wave shows that the potential for deriving information about the anisotropy from SH-wave data is significantly smaller than for the P-wave data. When the stacking velocity is determined from seismic data, it is influenced by lateral inhomogeneities, topographic effects or small-spread assumptions of the survey set-up, such that a velocity variation of 1% will not be resolvable. Hence, in the following we use the seismic P-wave data to determine the Thomsen parameter, δ, as a measure of anisotropy.
The anisotropic NMO velocities, VNMO, P, are derived from the analysis of the moveout, At, from layer interfaces in the seismic P-wave data, i.e. using the stacking velocity. To be able to derive the anisotropy parameter, δ, we need to know the zero-offset rms velocity, V RMS, ζ(0°), which can be derived from the depth of these layers. In order to obtain the depth of the layer interfaces we can combine the seismic data with other datasets (e.g. borehole or radar data). Therefore, we have to be able to identify identical layer interfaces in the seismic data and the other reference dataset (e.g. a radar dataset).
Care has to be taken here if only a few of many existing layers can be identified. In this case, calculating the zero-offset velocity from depth gives a mean zero-offset velocity and would, thus, underestimate the zero-offset rms velocity, V RMS P(0°), and, thereby, also the anisotropy. By identifying a number of layers the analysis of the anisotropy becomes more exact. Nevertheless, by combining the information from the seismic P-wave data (V NMO, P) and radar datasets (V RMS, P(0°)) we derive an effective δ parameter, as an average
over the depth of the identified layers (Reference TsvankinTsvankin, 1996, Reference Tsvankin2001),
with
When more than one layer is identified, the delta values, δ(i), for the different intervals can be calculated using Eqn (7), comparable to calculating interval velocities from rms velocities. However, these layers are still averaged layers, as it is only possible to identify layer interfaces where reflections exist. Thus, the parameters are still effective, averaged values compared to the ice-core COF measurements. Nevertheless, information about the changes in anisotropy over depth can be gained from P-wave data.
At Colle Gnifetti, we combine the seismic dataset with radar data, considered the reference, shown in Figure 4, that were measured close to the borehole location of the KCI ice core. The radar data (RAMAC, shielded 250 MHz antenna) show some coherent reflections down to the firn/ice transition (Fig. 4, grey line a), followed by a rather quiet zone and some noise above the bed reflector (grey line b). We link the bed reflection of the seismic data to that of the radar data (Fig. 4, grey line b). Additionally, the strong reflection around the firn/ice transition zone in the case of the ElViS P-wave data is linked to the vanishing of internal reflection horizons (Fig. 4, grey line a) that can be observed in the radar data around the firn/ice transition zone (Reference Konrad, Bohleber, Wagenbach, Vincent and VincentKonrad and others, 2013). We obtain the anisotropic NMO velocity, V NMO, P, from the seismic datasets and calculate the zero-offset rms velocity, V RMS, P(0°), from the depth of the layers derived from the radar data. With Eqn (6) the δ eff value can be derived and then the interval δ values (Eqn (7)). Hence, we are able to derive the anisotropic fabric for a two-layer case at Colle Gnifetti. From the derived δ values we can then estimate the effective cone opening angle of -46° for the first 27 m depth and an effective cone opening angle of 31° for the lower part of the ice column (Fig. 5b, solid black line).
The resulting opening angles are an estimate of the anisotropy. The analysis is influenced by: (1) the estimate of the reflector depth from radar data; (2) the calculation of zero-offset rms velocities from the estimated depth; (3) inaccuracy during the determination of stacking velocity from seismic data; (4) the identification of the stacking velocities as anisotropic NMO velocity; and (5) the definition of the cone opening angle. For example, a shift in the estimate of the reflector depth by 1 m up or down introduces a change in the resulting anisotropy. Estimating the depth of the internal layer at Colle Gnifetti from radar data 1 m deeper would result in opening angles of 40° for the upper 28 m and 34° below. A similar effect can be observed, when the bed reflection is estimated to be at 63 m depth, the depth estimate from the borehole radar data. This results in an opening angle of 27° instead of the 31° with the depth estimate of 62 m for the bed reflection. However, the -62 m ice thickness at Colle Gnifetti is a rather shallow example compared to polar ice masses where ice thicknesses are in the kilometre range. If it is possible to apply this method to reflection signatures in ice sheets where the overall thickness is much larger, the sensitivity towards small shifts in depth will decrease. Thus, from the combination of seismic and radar data the degree of existing crystal anisotropy within the ice can be derived.
At Colle Gnifetti the results from the seismic/radar data combination (Fig. 5b, solid black line) can be compared to the opening angles derived from the KCI ice core (Fig. 5b, dashed grey line). Here good agreement can be observed between the seismic-derived opening angle and the opening angle measured at the KCI ice core below 27 m depth. The anisotropy derived for the firn part is in contrast to our assumption of isotropy within this region for the comparison between anisotropic rms velocities, V NMO, ζ, and zero-offset velocity, V RMS, ζ(0°) (Fig. 6), calculated from the KCI ice-core data. The calculated difference of anisotropic NMO velocity and zero-offset velocity (7% for the P-wave bed reflection) cannot explain the complete depth difference between the derived depth of the ElViS P-wave data and the depth estimate of -62 m from the ice-core and radar data, with differences of 10% for profile 1 and 13% for profile 2.
As COF measurements were only available below the firn/ice transition, above we have assumed the isotropic state, as it is the most simple case. This assumption is not necessarily true. As a strong preferred fabric orientation is already developed at 30 m depth, observable in the KCI COF data (dashed grey line, Fig. 5b), it is most likely that anisotropy already exists within the firn part. Thus, it makes sense that we cannot derive the complete depth discrepancy observed from ElViS data with the velocity calculation from the KCI ice-core data and, also, derive an existing anisotropy within the firn column. Besides a preferred crystal orientation, an effect of anisotropy can also be introduced in the velocity analysis by a stack of fine layers. The effect of these fine layers is often described with a VTI model. At Colle Gnifetti such an effect can be caused by the density gradient in the firn. The influence of layering on the velocity analysis was investigated by Reference Grechka and GrechkaGrechka and Tsvankin (2002). They found that layering always causes a non-negative δ value, i.e. the anisotropic NMO velocity is higher than the zero-offset velocity. However, we derive a negative δ value for the firn part, i.e. the anisotropic NMO velocity is lower than the zero-offset velocity. Hence, we conclude that the observed anisotropy is not caused by the density gradient but rather by an already developed preferred crystal orientation within the firn. The development of crystal anisotropy in snow has been observed before (Reference Riche, Montagnat and MontagnatRiche and others, 2013). The reason for the development of anisotropy in the firn remains an open question.
Conclusion
We have investigated the reason for the difference in accuracy for the depth conversion between seismic P- and SH-wave stacked data from Colle Gnifetti. We used density, temperature and COF measurements from the KCI ice core to calculate P- and SH-wave velocities for the differently aligned fabrics over depth. To be able to use realistic velocity values for the upper 30 m, we derived a new relationship between density and S-wave velocities in firn. For the correction of the density for the P-wave we used the well-established relationship of Reference KohnenKohnen (1972). Thus, we are able to calculate anisotropic NMO velocities and zero-offset rms velocities for the multilayer case at Colle Gnifetti. We conclude that the difference between anisotropic NMO velocity, V NMO, ζ, determined from moveout analyses of reflections, and zero-offset velocity, V RMS, ζ(0°), needed for the depth-conversion, is 7% for the P-wave and 1% for the SH-wave for the ice/bed reflection at Colle Gnifetti. The exact values depend on the choice of elasticity tensor and the definition of the cone opening angle. These discrepancies do not explain the complete depth difference between the ElViS-derived glacier-bed depth from P-wave data and the depth estimate from the KCI ice-core and radar data. Thus, we conclude that a developed anisotropy may already exist within the firn column.
A difference also exists between the profile 1 and profile 2 discrepancies for ElViS-derived glacier-bed depth with the KCI ice-core length and radar data. This difference can also be seen by analysing the diving waves of profiles 1 and 2, with large variations in the travel times of the diving waves on profile 2, hence, in the firn part. Such lateral variations cannot be accounted for using the point measurements of the KCI ice core for velocity calculations. Nevertheless, both profiles suggest that anisotropy has a large influence on the P-wave moveout. The error introduced by assuming an isotropic state and using stacking velocities to derive depth-conversion velocities is thus no longer negligible.
Additionally, we have been able to show the potential of P-wave data in deducing information about the anisotropic crystal fabric. This is, of course, only possible for multiple layers when englacial reflections are strong enough to carry out a precise velocity analysis. Further, the depth of these reflections needs to be known, for which the seismic data have to be connected with other datasets, preferably radar data. Radar data have the advantage that the changes in COF have an influence on backscatter, but not so much on the velocity. Thus, they can be used to determine the depth of reflectors.
By combining the seismic P-wave data with radar data it is possible to derive information about existing anisotropic regimes in an ice column. This yields the opportunity to improve our understanding of the lateral distribution of anisotropic ice fabrics in ice sheets.
Acknowledgements
We are grateful to Air Zermatt, to the High Altitude Research Station Gornergrat, to the Department of Geography, University of Zürich, and for the invaluable logistic support of the staff at Cabanna Regina Margherita from the Club Alpino Italiano di Varallo/MBG Impresa. Financial support for this study was provided to O.E. by the Deutsche Forschungsgemeinschaft (DFG) ‘Emmy Noether’ programme grant EI 672/5-1. I.W. was supported by the Initiative and Networking Fund of the Helmholtz Association (HGF–VH-NG-802). We thank Pascal Bohleber, Reinhard Drews and Gunther Druivenga for support during the campaigns. We also thank two anonymous reviewers and S. Anandakrishnan for comments which greatly helped to improve the manuscript.
Appendix
Equations given by Reference BennettBennett (1968) for the calculation of P- (v p) and SH-wave (v sh) group velocities, depending on the incoming angle, θ, and the cone opening angle, ø, are
with variables
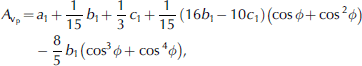
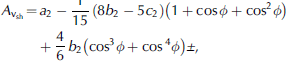
and parameters
а 1 =256.28 µm s ̶1,
b 1 =5.92 µm s ̶ 1,
c 1 =5.08 µm s ̶ 1,
a 2 = 531.40 µm s ̶ 1,
b 2=45.37 µm s ̶ 1,
c 2 = 15.94 µm s̶ 1.









