Published online by Cambridge University Press: 27 September 2013
In a recent paper on stylobate design in Doric temples I stated, with the minimum of evidence, certain working hypotheses on some of the factors restricting ancient Greek architectural design procedures. The present paper is, in part, an attempt to examine more closely the evidence for those hypotheses, but it also has a wider aim; it tries to thin out the almost numberless possible theories concerning the way in which Greek temples were planned, by looking at some of the technical restrictions felt by ancient architects, by stating and examining the consequences of certain hypotheses which seem to be widely, if tacitly, accepted by students of Greek architecture, and by suggesting how many of the propositions put forward by modern investigators may be tested, more or less rigorously perhaps, but nevertheless objectively.
Besides the abbreviations normal in BSA, the following are used:
(a) Bibliographical:
Aegina = A. Furtwängler, Aegina, das Heiligtum von Aphaia (1906).
Bouras = Ch. Bouras, I Anastilosis tis Stoas tis Vravronos (1967).
Corinth = American School of Classical Studies at Athens, Corinth, Results of Excavations … (1929— ).
Didyma ii = Rehm, A. (ed. T. Wiegand), Didyma ii (1958).Google Scholar
EAD = École française d'Athènes, Exploration archéologique de Délos (1909-).
FAD = École française d'Athènes, Fouilles de Delphes (1902-).
Heath = T. L. Heath, History of Greek Mathematics (1921).
KP = R. Koldewey, O. Puchstein, Griechische Tempel in Unteritalien und Sicilien (1899).
Martin = Martin, R., Manuel d'architecture grècque i (1965).Google Scholar
Olympia = E. Curtius, F. Adler, Olympia, Ergebnisse … (1890–96).
Orlandos = A. Orlandos, Ta ilika domis ton arkhaion Ellinon (1955–8).
Penrose = F. C. Penrose, Investigation of the Principles of Athenian Architecture (2nd edn., 1888).
Roux = G. Roux, L'Architecture de L'Argolide aux iv et iii siècles av. J.-C. (1961).
(b) Elements of a columnar order:
A = Architrave height
Ab = Abacus height
AbW = Width of abacus
Cor = Cornice height
Cp = Capital height
D = Lower column diameter on arrises
F = Frieze height
H = Column height
I = Axial intercolumniation
L = Length over stylobate
mod. = module
OL = Over-all length
OW = Over-all width
S = Stylobate breadth from back to front
T = Triglyph width
W = Width over stylobate
Where the size of an element on the flank of a building differs systematically from that on the front, the letter W (or L), written subscript, indicates that the abbreviation refers to the front (or flank) of the building.
1 BSA lxix (1974), 61–86.
2 Guido, M., Sicily, An Archaeological Guide (1968) 123–5.Google Scholar
3 Thus almost all the colossal temples were either never finished or left unfinished for centuries. The desire for economy might lead to a non-peripteral temple, but the structural methods were unchanged, and in so far as there were columns at all, the forms were normally the same as in a peripteral one.
4 vi. 2. 2.
5 Any exceptional procedures will be best distinguished and understood if we know the methods of design normally in use, just as exceptional forms are distinguished and interpreted on the basis of a knowledge of the forms normal to Greek architecture. We should therefore concentrate initially on understanding the general procedures, rather than the exceptions and modifications to be found in individual buildings.
6 AJA lxxii (1968) 188–9.
7 Krauss, F., Paestum, die griechischen Tempel (1943) 62–3.Google Scholar
8 Koldewey and Puchstein (KP passim) regarded the average diameter as the significant one in most Sicilian and South Italian temples.
9 Compare the two different rules which would give a stylobate length 2 ![]() times its width to a temple with 6 × 14 columns (BSA lxix (1974) 61–86).
times its width to a temple with 6 × 14 columns (BSA lxix (1974) 61–86).
10 Even the fundamental study of Greek design methods by Bundgaard (J. A. Bundgaard, Mnesicles. A Greek Architect at Work (1957)) is based primarily on the Propylaia. One exception is the attempt by Koldewey and Puchstein to work out the basic systems of the Sicilian and South Italian temples, but this is only one in quite a general way. Hambidge's attempt to demonstrate the use of dynamic symmetry in Greek architecture deals mainly with the Parthenon, with much less thorough studies of other buildings (J. Hambidge, The Parthenon and other Greek Temples: their Dynamic Symmetry (1924).
11 One restrictive factor which we have not considered is the occasional need to re-use material from another building, as in the Parthenon and the fourth-century temple of Apollo at Delphi. Such cases will normally be readily recognizable, however.
12 Besides the general probabilities that will emerge in the course of this study (as for instance in the treatment of fractions), there is a positive argument for the relevance of Vitruvius to the study of classical Greek architecture in the discrepancy between the design method suggested by De Arch. i. 1. 4 and i. 2. 2 and that implied in De Arch. Books iii and iv. In i. 1.4 and i. 2. 2, Vitruvius assumes that plans and elevations of a proposed building will be drawn, and that would appear to have been contemporary practice, for Roman scale plans of buildings have survived. However, plans and elevations are nowhere mentioned in Books iii and iv; they are not necessary to the application of the rules (cf. p. 63 below); and the absence of detailed prior planning is strongly suggested by phraseology such as ‘The shafts of the columns having been erected, the rule for the capitals will be as follows’ (iii. 5. 5). Some of Vitruvius' rules clearly go back only to the Hellenistic period (such as those for the pseudo-dipteral plan and for eustyle columnspacing), but it is unlikely that a new procedure of the sort implied by Books iii and iv would have been developed for Hellenistic temples, if earlier temples were already designed by means of plans and elevations drawn to scale; so this design procedure probably goes back at least to the fifth and fourth centuries, and perhaps to the beginning of Greek monumental architecture.
13 IG ii2. 1668; Jeppesen, K., Paradeigmata (1959) 69–101.Google Scholar
14 Vitruvius iii. 3. 8.
15 Vitruvius iv. i. 6; Vitruvius iv. 1.3 talks of an earlier stage before the adoption of rules of proportion.
16 See, for example, in the proportional analysis of some early Doric capitals in BCH lxxxvii (1963) 639–52.
17 vi. 2. 2.
18 On the subdivision of Greek measuring instruments, see below, pp. 90 ff. Gudea's ruler has single dactyls divided into 2, 3, 4, 5, and 6 parts (i.e. down to 0·0028 m.: L. W. King, History of Sumer and Akkad (1923) figs. 64–5), and an Egyptian cubit rule has successive single dactyls divided into 2, 3, 4… 14, 15, 16 parts (i.e. down to 0·0012 m.: Berriman, A. E., Historical Metrology (1953) 76Google Scholar).
19 For references to paradeigmata see Orlandos ii. 268 n. 3.
20 Penrose 111–16.
21 J. Hambidge, The Parthenon and other Greek Temples: their Dynamic Symmetry (1924).
22 C. Tiberio, Mnesicle. L'Architetto dei Propilei (1964).
23 Thus the flexibility of Lloyd's system, to which Penrose admiringly draws attention (Penrose 116), should be regarded as an argument not for, but against, its importance.
24 This is, of course, an exaggerated example, but in some cases the explanation offered does seem to be little more than a conversion into other units and types of fraction, as, for instance, in Hesperia Suppl. v (1941) 93.
25 The distinction is rightly made by Scholfield, P. H., The Theory of Proportion in Architecture (1958) 18.Google Scholar
26 Corbusier, Le, The Modulor (Eng. edn., 1954) 90Google Scholar, and note the procedure suggested ibid. 158–60.
27 Plato, Phlb. 64d–e, Tim. 87 c–d; Aristotle, Metaph. 1078a36, Poet. 1450b35, Top. 116b21.
28 Plato, Phlb. 51 c–d.
29 Plato, Rep. vii. 529 C–530 a.
30 Demokritos and Anaxagoras were inspired by Agatharchos' scene painting (Vitruvius vii. praef. 11), and Chrysippos quoted Polykleitos' canon (Galen, Placit. Hipp. et Plat. 5).
31 i. 1. 3–16.
32 9. praef.
33 Vitruvius i. 1. 12.
34 Vitruvius iii. i. 5–8; see also TABLE 2, p. 83. Scholfield, P. H. (The Theory of Proportion in Architecture (1958) 16–32Google Scholar) has argued that a more sophisticated theory lies behind Vitruvius' words, but he admits (26) that the rules do not often follow the proposed theory.
35 Vitruvius iii. 3. 12; iii. 5. 8–9; vi. 2. 1–4.
36 Vitruvius vi. 1. 6. Six, as we have seen, is listed by Vitruvius as a perfect number, but the ratio chosen for the Ionic column (iv. 1. 7) was 1:8, later 1:9.
37 Vitruvius iv. 1. 8.
38 Panofsky, E., Meaning in the Visual Arts (1955) 62–72.Google Scholar
39 Pliny, , NH xxxiv. 61.Google Scholar Here again the idea of symmetria in general seems to have been important, but no theoretical basis is suggested for the specific rules adopted.
40 Plato, Soph. 235e–236a; Tzetzes, , Chil. viii. 358Google Scholar (Overbeck, Schriftquellen, no. 772).
41 The fourth-century Treasury of Kyrene at Delphi has been held to embody higher mathematical theory (FD, J. Bousquet, Le Trésor de Cyrène (1952), passini), but see Dinsmoor's, review (AJA lxi (1957) 402–11).CrossRefGoogle Scholar Dinsmoor shows that the dimensions of the building, as worked out by Bousquet, are suspect (and it is indeed doubtful whether the building is well enough preserved to give the required accuracy and certainty); that much of the mathematical theory depends on the conversion of these measurements into feet and dactyls, in terms of a foot standard which is not certain to have existed; and that many of the proportional relationships held to involve irrationals can be explained in simpler terms (thus the ratio √2:√3 is virtually the same as ![]() (0·816… as against 0·818…), so that, e.g., the upper diameter of the column was probably derived from the lower diameter by taking
(0·816… as against 0·818…), so that, e.g., the upper diameter of the column was probably derived from the lower diameter by taking ![]() parts out of
parts out of ![]() (cf. Vitruvius iii. 3. 12; 4·5D/5·5 = 0·455 m., d = 0·456 m.), rather than by using the ratio √2:√3).
(cf. Vitruvius iii. 3. 12; 4·5D/5·5 = 0·455 m., d = 0·456 m.), rather than by using the ratio √2:√3).
42 Vitruvius iv. 3. 3–10.
43 Vitruvius iii. 5. 1–15.
44 e.g. by G. Roux in Roux 326–7; by the present author in BSA lxiii (1968) 171.
45 Vitruvius iv. 7–8. The rules of human proportion attributed to Chrysippos and through him to Polykleitos (Galen, Piacit. Hipp, et Plat. 5 (ed. Müller 425)), appear also to form a successive system, relating finger to finger, all fingers to palm and wrist, palm and wrist to forearm, forearm to upper arm. The final words ![]() in fact ‘everything to everything else’, suggests, if taken literally, a modular system. The words, however, are probably not those of Polykleitos himself, but of a summarizer, who perhaps did not notice the difference, or was more interested in the concept of a commensurability than in the precise nature of the series of rules.
in fact ‘everything to everything else’, suggests, if taken literally, a modular system. The words, however, are probably not those of Polykleitos himself, but of a summarizer, who perhaps did not notice the difference, or was more interested in the concept of a commensurability than in the precise nature of the series of rules.
The rules of human proportion given in Vitruvius iii. 1. 2 are neither modular nor successive. They may perhaps be called fractional, since the dimensions of all the main elements of the figure are defined as submultiple fractions of the total figure height.
46 Vitruvius iii. 5. 8.
47 Hence, instead of trying to arrange the proportions of Doric capitals to form a continuous series, we should try to arrange them into a greater or smaller number of discrete groups.
48 That is if the commonly accepted equation of I ft. = 0·326 m. is valid for the temple.
49 e.g. Pliny, NH xxxvi. 23, 56, 178–9.Google Scholar Especially valuable is the record of the ratios used in the Old Temple of Artemis at Ephesos. This must go back to the fourth century B.C., when the temple was destroyed, and since it is unlikely that anybody in the fifth or fourth century took the trouble to re-measure the building, Pliny's information probably comes from the book on the temple written by its architects, Chersiphron and Metagenes (Vitruvius vii. praef. 12). It therefore represents not simply fact, but intention. The only literary evidence for incommensurable ratios is the occurrence twice of the ratio 1:√2 in Vitruvius (iv. 1. 11, vi. 3. 3). It seems unlikely that these are the meagre remains of a much more widespread use of incommensurable ratios in earlier Greek architecture, for the rules in question deal with the Corinthian capital and the Roman atrium, neither of which can be regarded as basic to Classical Greek architecture.
50 The rules of Polykleitos in the passage of Galen cited above (n. 45) involved symmetria, which would naturally mean normal commensurability, not commensurability in square. The rules for the human figure given by Vitruvius (iii. 1. 2) certainly involve commensurable ratios, and probably go back to the fifth or fourth century B.C. (on the date see n. 125 below). Similarly, when Plato speaks of geometrical designs drawn by artists (Rep. vii. 529 d–30 a), the ratios he imagines they might display (but not embody) are 1:1, 1:2, or some other commensurable ratio ![]()
![]() However, the argument here is that the stars seen in the heavens, although very beautiful, can only serve as diagrams for the true science of astronomy, just as geometrical diagrams, even if beautifully drawn by professional artists, can never contain true mathematical entities; it is uncertain whether Plato meant ‘geometrical diagrams such as are drawn by artists (as a basis for their works of art)’ or ‘geometrical diagrams, even if they were to be drawn by artists (for the use of geometers)’. Both are possible interpretations of the Greek, and both would suit the argument
However, the argument here is that the stars seen in the heavens, although very beautiful, can only serve as diagrams for the true science of astronomy, just as geometrical diagrams, even if beautifully drawn by professional artists, can never contain true mathematical entities; it is uncertain whether Plato meant ‘geometrical diagrams such as are drawn by artists (as a basis for their works of art)’ or ‘geometrical diagrams, even if they were to be drawn by artists (for the use of geometers)’. Both are possible interpretations of the Greek, and both would suit the argument
51 Hesperia ix (1940) 22.
52 Vitruvius iii. 3. 2–5, iii. 3.10; the eustyle system stands outside this rule.
53 Vitruvius iii. 5. 8, provided that fractions of a foot are neglected in the term H/5.
54 Note, for instance, the lack of clarity in Morgan's comparison of Vitruvius’ rules for column taper with actual Greek practice (Vitruvius, , The Ten Books of Architecture, trans. Morgan, M. H. (1914) 85.Google Scholar The figures given by Morgan are set out below, with the simple decimal equivalents in brackets beside them:
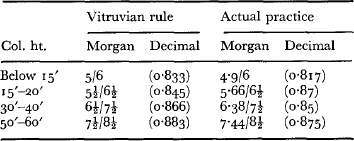
It is clear from the decimal equivalents that the second example completely breaks Vitruvius' rule, and that the others all taper more strongly than they should according to Vitruvius. These three approximate more closely, in fact, to other terms in the Vitruvian series: ![]() (0·818),
(0·818), ![]() (0·845), and 7/8 (0·875).
(0·845), and 7/8 (0·875).
55 Timaeus 36 b.
56 Herodian, Peri ton Arithmon (see Stephanus, H., Thesaurus Linguae Graecae (Didot edn., Paris, 1865) viii. 345Google Scholar, says that the system was used in the record of Solon's legislation. Nothing as early as that has survived, but there are acrophonic numerals on late sixth-century sima sections from near Kaulonia (Jeffery, L. H., The Local Scripts of Archaic Greece (1961) 258Google Scholar). What appear to be acrophonic numerals occur on marble roof tiles from the Acropolis at Athens, and these may belong to the Pisistratean buildings there (Peppa-Delmazoglou, N. T. in Charisterion A. Orlandos iv (1967–1968) 369–850Google Scholar).
57 For fractions of a dactyl see pp. 78 ff. below.
58 Hackl, R., in Münchener archäologische Studien (1909) 79–82, 92–4Google Scholar; the explanation may well be correct if the acrophonic numerals were already used in Athens in the latter part of the sixth century (see n. 56 above).
59 Mayser, E., Grammatik der griechischen Papyri i (1906) 51.Google Scholar![]() = 1,000 drachmae occurs in a papyrus of 311 B.C. (David, M., van Groningen, B. A., Papyrological Primer (3rd edn., 1952) 42 no. 25Google Scholar, 11. 4, 11, 12. For mathematical texts see Heath, i. 42–3.
= 1,000 drachmae occurs in a papyrus of 311 B.C. (David, M., van Groningen, B. A., Papyrological Primer (3rd edn., 1952) 42 no. 25Google Scholar, 11. 4, 11, 12. For mathematical texts see Heath, i. 42–3.
60 Woodhead, A. G., The Study of Greek Inscriptions (1967) 109–11.Google Scholar
61 IG ii2. 760.
62 Hermes xxix (1894) 248–80; SIG 3 no. 46.
63 Fine, J. V. A., Horoi (Hesperia, Suppl. ix (1951)), esp. 48–9.Google Scholar
64 Probably official: IG iia. 2777; IG xii5. (5) 99; AM xxiii (1898) 2–3, no. 1. Probably unofficial: Corinth i. 4 (1954) 64, pl. 15. 1 (the large letters at the bottom are probably Χ, ![]() and
and ![]() ); Hesperia xxxvii (1968) 243 no. 5; IG ii2. 2779–80; cf. also the die, AM xxiii (1898) 17. 4.
); Hesperia xxxvii (1968) 243 no. 5; IG ii2. 2779–80; cf. also the die, AM xxiii (1898) 17. 4.
65 Hesperia iv (1935) 515–17; for the date, ibid. 497.
66 On the Athenian Treasury at Delphi (FD, Audiat, J., Le Trésor des Athéniens (1933) 35)Google Scholar the numbers are 5 and 8 (not 5 and 9 as Orlandos 158), and on the Propylaia at Athens (Orlandos 159) the number is 10 not 2 (as Martin i. 225). The same system is used on parts of the Vix krater (the numbers are 1–7; Rend. Linc. ser. viii. 18 (1963) 1–19).
67 The non-numeral character of the first ten letters of the alphabet cannot, of course, be demonstrated, but the ψ on a drum of the fourth-century temple of Apollo at Delphi (FD, Courby, F., La Terrasse du Temple i (1915) 88Google Scholar) and the Χ on the Old Temple at Sounion (Orlandos 160) can hardly be numerals, since they would mean 700 and 600, numbers which are much too high. The letters on the Sikyonian Treasury at Olympia are probably masons' marks, not position indicators: pairs of letters as well as single letters are used, and although ΙΕ could be 15 and ΠΑ perhaps 81 (although too large a number for so small a building), ΑΔ and ![]() cannot be numerals (Olympia (1896) no. 668).
cannot be numerals (Olympia (1896) no. 668).
68 EAD vii. 1, Vallois, R., Le Portique de Philippe (1923) 63–6Google Scholar; for the date, ibid. 154–63.
69 Acrophonic numerals occur on the Treasury of Kyrene at Delphi (FD, Bousquet, J., Le Trésor de Cyrène (1952) 40 Pll. 15. 1, 17. 6).Google Scholar
70 Hermes xxix (1894) 348–80; Jeffery, L. H., The Local Scripts of Archaic Greece (1961) 327.Google Scholar
71 SIG 3, no. 46 (the Halikarnassos inscription already mentioned); OGIS, no. 46. 6 (Halikarnassos, 3rd cent, B.C.); Collitz-Bechtel, , Sammlung der griechischen Dialektinschriften iii. 2 (1900) no. 5616Google Scholar (Smyrna, c. 300 B.C.); Schwyzer, E., Dialectorum Graecorum Exempta Epigraphica (1923), no. 709aGoogle Scholar (Klazomenai, 3rd cent. B.C.).
72 Heath i. 41–4. The briefest and clearest notation was with the denominator above and the numerator below, reversing our current system.
73 Didyma ii. nos. 39–43 and 48. Not surprisingly, the Egyptian system is the only one found in papyri (Mayser, E., Grammatik der griechischen Papyri i (1906) 52–3Google Scholar). It seems also to have been used by builders working at Alexandria. On an unfluted column-drum was engraved: ![]()
![]() which is presumably to be interpreted as: diameter
which is presumably to be interpreted as: diameter ![]() ft. (= 0·678 m., using the Ptolemaic foot of c. 0·35 m.),height
ft. (= 0·678 m., using the Ptolemaic foot of c. 0·35 m.),height ![]() ft. (= 1·497m.). The actual diameter and height of the drum are 0·68 m., and 1·51 m. See Hoepfner, W., Zwei Ptolemaierbauten (AM, 1971) 69–70Google Scholar, where a different interpretation is offered which does not explain all the symbols recorded. The date is probably c. 230–220 B.c.
ft. (= 1·497m.). The actual diameter and height of the drum are 0·68 m., and 1·51 m. See Hoepfner, W., Zwei Ptolemaierbauten (AM, 1971) 69–70Google Scholar, where a different interpretation is offered which does not explain all the symbols recorded. The date is probably c. 230–220 B.c.
74 The discussion which follows is based primarily on the references given in LS 9. Although all occurrences of commonly used expressions are not noted there, the absence of a word from LS 9 is reasonable evidence that it does not occur in surviving ancient Greek. The following pages have benefited from the help of my colleague D. B. Robinson, who has pointed out several relevant passages which I had missed; he does not, however, share all the views expressed here.
75 See LS 9 under the appropriate words ![]()
![]() Archim., Aren. ii. 4, iv. 1).
Archim., Aren. ii. 4, iv. 1).
76 Eudox., Ars 16. 11: Hippoc. Oct. 13.
77 Archim., Aequil.
78 Archim., Circ. 3.
79 Note ![]() (Plato, Leg. 956 c and Alexios in Athenaios iii. 117 e). Cf. also IG 1675. 18.
(Plato, Leg. 956 c and Alexios in Athenaios iii. 117 e). Cf. also IG 1675. 18.
80 ![]() (3rd cent.),
(3rd cent.), ![]() See LS9 under the appropriate words. The fractions marked with an asterisk are not used in this sense before c. 300 B.C.
See LS9 under the appropriate words. The fractions marked with an asterisk are not used in this sense before c. 300 B.C.
81 ![]() (IG 310 al.),
(IG 310 al.), ![]() (Thuc. viii. 10). Note also
(Thuc. viii. 10). Note also ![]() (IG ii2. 1675. 18) of a special type of bronze.
(IG ii2. 1675. 18) of a special type of bronze.
82 Hippoc, Inst. 26, Isoc, xii. 177, Plato, Leg. vi. 784a, Xen., Cyr. ii. 1. 6, vi. 3. 2; ![]() Plato, Rep. ii. 369 e, 370a;
Plato, Rep. ii. 369 e, 370a; ![]() Plato, Apol. 36 b (etc.);
Plato, Apol. 36 b (etc.); ![]() Plato, Leg. xii. 956 c;
Plato, Leg. xii. 956 c; ![]() Aristoph., Thesm. 555.
Aristoph., Thesm. 555.
83 Plato, Rep. viii. 546 c, Tim. 36 a, b.
84 Xen., Vect. iii. 9; Dem. xxxiv. 23, 1. 17; IG i2. 377.
85 Ptol., Harm. i. 15.
86 There are expressions for 2:3 ![]() 3:4, 4:5, 8:9 (LS9 s.v.
3:4, 4:5, 8:9 (LS9 s.v. ![]() ); the terms first occur in Aristotle.
); the terms first occur in Aristotle.
87 Vitruvius iii. 1. 6; Aesch., Suppl. 1070.
88 Thuc. i. 104, Aeschin. iii. 143; Plato, , Rep. ii. 370 aGoogle Scholar, IG ii2. 1675. 19–20; cf. IG ii2. 1670. 29–32. In Dem. lix. 101, ![]() is used without
is used without ![]() being expressed.
being expressed.
89 Thuc. i. 10, Empedocles in Diels, H., Kranz, W., Fragmente der Vorsokratiker (6th edn., 1951–1952), fr. 31 B96.Google Scholar
90 e.g. Archim., Aequil. 2. 10 (ed. Heiberg, p. 210).
91 Heath i. 51.
92 Hdt. ii. 36. 4, Aristoph., Vesp. 656–64, Lysias, fr. 50, Dem. xviii. 227, 229, Alexis in Athenaeus iii. 117e, Polyb. v. 26. 13, Diog. Laert. i. 59, Plutarch, Mor. 812e.
93 IG ii2. 2777; Heath i. 50–1; RE Suppl. iii (1918) 10–11; Hesperia xxvi (1957) 271–87; xxxiii (1964): 146–67.
94 Hesperia xxxiv (1965) 131–47, esp. 138–40. Add to the references for large stone gaming-tables in sanctuaries: AM xxiii (1898) 1–14; note also two such tables at Goritsa, (AAA v (1972) 492Google Scholar, fig. 9). For the large sums of money involved, compare the die from the Acropolis, Athenian (AM xxiii (1898) 14)Google Scholar, and the fortunes lost by Alkibiades, son of Alkibiades (Lysias xiv. 27) and by Hegesandros and Timarchos (Aeschin. i. 95).
Two further points in favour of the gaming-board interpretation may be added. On the abacus hypothesis, the central cross-line on the Salamis table is normally taken to separate the pebbles representing units, tens, hundreds, etc., from those representing fives, fifties, five hundreds, etc.; but in that case only one or two pebbles would ever have to be placed above it, as against four or five below it, so that the cross-line should not have been centrally placed. In our ignorance of the way Greek board-games were played, no full explanation for die cross-line can be offered on the gaming-board hypothesis either, but on general grounds a central cross-line would not be inappropriate to a competitive board-game for two players. The gaming-board hypothesis also allows die best explanation of the fact that the Salamis table has two sets of acrophonic numerals facing in opposite directions—the players sitting opposite each other each used a set of numerals to record their winnings (or losses), and the third set of numerals may have been used to record the stakes for the game currently in play.
The only abacus interpretation which takes both these difficulties into account is that of Menninger, K., Zahlwort und Ziffer (2nd edn., 1958) 109Google Scholar, who suggests that two men sat opposite each other to check each other's calculations, as with some medieval accounting tables (ibid. 153–6); the central cross-line would then be to separate the two calculating areas, while the two opposite-facing rows of numerals are self-explanatory. If this is how the Salamis table was used, however, it is surprising that the two calculating areas were not kept more separate, as in the medieval examples; the second calculation would be more likely to create confusion than correction. Also the third set of numerals at one end is unexplained; Meninger uses it to set out the multiplier in his example, but the numerals here, too, are for a sum of money, not a number, and in any case one would expect this row to be duplicated for the benefit of die second calculator.
95 IG xii (7). 282.
96 IG xii (5). 99; Hesperia xxxvii (1968) 241–3.
97 So all the references in n. 92 above, except Hdt. ii. 36. 4. The context is different in Aesch., Agam. 570 and Eur., Rhes. 309–10, but the image of accounting may well be intended.
98 So Hesperia xxxiii (1964) 147, 150; but see the descriptions of the Roman abacus in Daremberg-Saglio, s.v. ‘abacus’, RE Suppl. iii (1918) 5–10 and Heath i. 47.Google Scholar
99 Heath i. 13–16. Note also [Hero], Definit. 135. 6 (ed. Heiberg, p. 98): ‘Logistike treats one as the least in a group of things of the same type; it takes … one drachma in a number of drachmae as indivisible, even though as a coin it can be divided.’ This does not coincide with the practice in either the genuine or the spurious works of Hero, so presumably refers back to earlier ideas.
100 Phlb. 55 d–57 a. ![]() here includes not only building but also shipbuilding and other carpentry.
here includes not only building but also shipbuilding and other carpentry.
101 Heronis Alexandrini Opera v (ed. Heiberg, , Leipzig, 1914) praef. 21–35.Google Scholar
102 In both respects they contrast with the Metrica, which is probably a genuine work (Heronis Alexandrini Opera iii (ed. Schöne, , Leipzig, 1903) praef. 11–12Google Scholar).
103 Geometrica 20. 12.
104 Ster. i. 21. 1. Similar mistakes could occur in the Hellenistic period (e.g. Diayma ii. nos. 39, 54–5). Of the thirteen multiplications in Diayma ii. nos. 39–41 where all three terms are preserved, ten are correct (in six of these no fractions are involved). The other two errors result from writing down the wrong numeral.
105 De Mens. 28. 1.
106 The list may not be absolutely complete. It is based on the footnotes to Heiberg's edition of the works (n. 101).
107 Ster. i. 31. 2; ii. 22; ii. 57. 2; ii. 59. 4; De Mens. 27; 28. 1; 48.
108 Ster. i. 41. 1; i. 87. 2; ii. 1. 2; ii. 59. 3; ii. 60. 4; ii. 60. 5; ii. 63. 4; ii. 64. 3; De Mens. 28. 1 (twice); 38.
109 Ster. i. 67. 2; ii. 11; ii. 66. 4 (twice); De Mens. 28. 2 (twice); 52.
110 Ster. ii. 66. 5.
111 Ster. i. 51. 2; i. 76; i. 80; i. 81; i. 91. 1; ii. 10; ii. 60. 5; De Mens. 28. 2 (twice); 48.
112 Ster. i. 36. 2; i. 60; i. 66; i. 68; i. 69; i. 82; i. 86. 2; ii. 1. 2; ii. 10; ii. 16; ii. 66. 3; ii. 60. 4.
113 Ster. i. 36. 2; i. 68; ii. 1. 2; ii. 60. 4; ii. 66. 3.
114 Ster. i. 60; i. 66; i. 69; i. 82; i. 86. 2; ii. 1. 2; ii. 10.
115 Ster. i. 21. 11 (twice); ii. 11; De Mens. 38.
116 iv. 1. II; vi. 3. 3.
117 iii. 3. 7; iv. 3. 3.
118 iii. 3. 11—the diameter of an angle column to be increased by ![]()
119 iii. 3. 10; iii. 5. 8; cf. iii. 3. 12.
120 vi. 3. 5.
121 ![]() iii. 5. 11, iv. 6. 4;
iii. 5. 11, iv. 6. 4; ![]() iv. 6. 6.
iv. 6. 6.
122 ![]() iv. 3. 6) iv. 6. 5; dempta tertia: vi. 3. 5, vi. 3. 6; ‘divide X into 3 parts and take 2’: v. 1. 2, vi. 3. 3.
iv. 3. 6) iv. 6. 5; dempta tertia: vi. 3. 5, vi. 3. 6; ‘divide X into 3 parts and take 2’: v. 1. 2, vi. 3. 3.
123 See above.
124 See p. 64 above.
125 Vitruvius iii. 1. 2–3. Kalkmann, A. (Berl. Winck. Prog. xxxv (1893) 42–5)Google Scholar argued that these rules are likely to derive from Euphranor, whose work on symmetry was directly or indirectly known to Vitruvius (vii. praef. 14). J. E. Raven argues that they derive from Polykleitos, (CQ N.s. i (1951) 147–52)Google Scholar, but with less probability in view of their difference from the system attributed to Polykleitos by Galen (n. 45 above).
126 Vitruvius x. 10–11. i. For the system see Schramm, E. in SB. BerlAkad. 1917, 719.Google Scholar The signs (except for ι![]() =
= ![]() and S =
and S = ![]() ) are the Greek alphabetic numerals, but they express not the denominator, but the numerator, with the constant denominator of 16 understood. The convenience of using a constant denominator was appreciated by Hellenistic astronomers (who used a sexagesimal system) and by the Romans (who used a standard division into 12ths).
) are the Greek alphabetic numerals, but they express not the denominator, but the numerator, with the constant denominator of 16 understood. The convenience of using a constant denominator was appreciated by Hellenistic astronomers (who used a sexagesimal system) and by the Romans (who used a standard division into 12ths).
127 See p. 79 above.
128 v. 1. 6–10.
129 See n. 13 above.
130 Olympia ii (1892) 19; Wiegand, T., Schrader, H., Priene (1904) 86–7, 101–5.Google Scholar
131 Dinsmoor, W. B., The Architecture of Ancient Greece (and edn., 1950) 54 n. 3Google Scholar, 161 n. 1, 195 n. 1, 199 n. 1, 232 n. 2, 229 n. 2; id., in Atti dei VII Congresso Internazionale di Archeologia Classica i (1961) 357–60; for a third foot standard in an architectural context see note 73 above.
132 At Epidauros the accounting suggests that the builders were paid per contract, rather than at a standard rate per foot or cubic foot (Burford, A., Greek Temple Builders at Epidauros (1969) 191–8Google Scholar).
133 Didyma ii. nos. 20–44.
134 [Hero], Tab. Her. 4. 4 8nd 5. n mentions a ![]()
![]() and a
and a ![]() their length is unknown, but could be slightly larger than normal (like a ‘baker's dozen’ of 13) to allow for this problem. Since Greek architects seem to have worked in feet radier dian cubits, however, these special cubits probably do not relate to classical Greek architectural practice.
their length is unknown, but could be slightly larger than normal (like a ‘baker's dozen’ of 13) to allow for this problem. Since Greek architects seem to have worked in feet radier dian cubits, however, these special cubits probably do not relate to classical Greek architectural practice.
135 M. Lang, M. Crosby, The Athenian Agora X, Weights, Measures and Tokens (1964).
136 IG ii2. 1013.
137 ID 502. 24. Some doubtful light on the lengm of the orguia is shed by an inscription ![]() on the central wall of the South Stoa at Delos, (BCH xxvi (1962) 545).Google Scholar If this refers to the length of the building (72·47 m. over all; EAD, Vallois, R., Le Portique de Philippe (1923) pl. 1)Google Scholar, it would imply an orguia of not more than 1·541 m., and so a foot of not more than 0·2501 m!
on the central wall of the South Stoa at Delos, (BCH xxvi (1962) 545).Google Scholar If this refers to the length of the building (72·47 m. over all; EAD, Vallois, R., Le Portique de Philippe (1923) pl. 1)Google Scholar, it would imply an orguia of not more than 1·541 m., and so a foot of not more than 0·2501 m!
138 BCH vi (1882) 139; xxxi (1907) 72.
139 Bacon, J., Clark, F., Koldewey, R., Investigations at Assos (1902–1921) 71, 73.Google Scholar The slot lengths are: AB c. 2·32 m., CD c. 0·518 m., EF 0·367 m., GH 0·485 m. If these slots did hold length standards and their lengths bear some relation to the standards they held, then EF could have held a Pergamene-Ptolemaic foot of c. 0·35 m., GH an ‘Ionic’ cubit of c. 0·44 m., and CD a ‘Doric’ cubit of c. 0·49 m. However, AB is too long to be an orguia unless derived from a foot of c. 0·38 ft. It is dierefore perhaps more likely that the slots held not general length standards, but standard lengths for specific objects used, like the tiles, in building (the tile dimensions do not come out as round numbers of feet of any of the ‘accepted' sizes, either).
140 There is a good photograph of the slab in Bandinelli, R. B.et al., The Buried City: Excavations at Lepcis Magna (1966) pl. 69.Google Scholar A much more accurately set out standard cubit, probably of Ptolemaic or Roman date, is described by Petrie, F., Ancient Weights and Measures (1926) 40.Google Scholar
141 Kraay, C. M., Hirmer, M., Greek Coins (1966) 17.Google Scholar
142 M. Lang, M. Crosby, op. cit. (n. 128) 18–21.
143 R. Meiggs, D. Lewis, Greek Historical Inscriptions (1969) no. 45.
144 Robinson, D. M., Graham, J. W., Olynthus viii (1938) 45–51.Google Scholar
145 BSA lxviii (1973) 81–3.
146 Vitruvius iv. 3.
147 It has often been noticed, for instance, that the intercolumniations of the Parthenon are much less accurately set out, with variations of up to 0·048 m. (Penrose, pl. 4).
148 e.g. IG i2. 372E4; for other references see Orlandos ii. 140 n. 1.
149 Ap. Rhod. i. 724.
150 Aristoph., Ran. 799.
151 See Hultsch, F., Metrologicorum Scriptorum Reliquiae (1894–1896)Google Scholar, index.
152 Hero, , Dioptra (ed. Schöne, , 1903) 262.Google Scholar 12, 292. 18.
153 Ibid. 254. 14, 262. 13, 270. 15.
154 Clark, D., Plane and Geodetic Surveying i (5th edn., 1958) 51.Google Scholar
155 Hultsch, F., Metrologicorum Scriptorum Reliquiae ii (1896) 113.Google Scholar 12; cf. Hor., Car. ii. 15. 14–16. For the variant lengths, F. Hultsch, op. cit. 137. 6 (Isidoras).
156 Pétrie, F., Ancient Weights and Measures (1926) 38–40.Google Scholar
157 Ibid. 48. Cf. Grenier, A., Manuel d'archéologie galloromaine iii. i (1958) 36.Google Scholar
158 Thus Dinsmoor, (Atti del VII Congresso Internazionale di Archeologia Classica i (1961) 357)Google Scholar noted that metre sticks sold in Athens varied by up to 0·0015 m.; yet modern official standards of length would not vary by a tenth of that amount.
159 Some ancient architects' rules were very finely divided (see above, note 18); there is no evidence that such rules were used by Greek architects, but even if they were, it would not be possible to specify, as such, dimensions which could not be measured out with the builders' rules.
160 Most inscriptions show a clear preference of measurements in feet and palms, but contrast IG ii2. 1678.
161 e.g. Hesperia ix (1940) 46; Hesperia Suppl. v (1941) 93.
162 Cf. AJA xxvi (1932) 263.
163 See note 140 above.
164 IG ii2. 1671. 45, 1675. 15. The convenient compound form ![]() is not recorded before c. 200 B.c. (Philo, Bel. 63. 42, 65. 3, 65. 23 with three other later Hellenistic instances noted by LS? 8).
is not recorded before c. 200 B.c. (Philo, Bel. 63. 42, 65. 3, 65. 23 with three other later Hellenistic instances noted by LS? 8).
165 Didyma ii. no. 48 (![]() feet =
feet = ![]() ft. = 6 ft.
ft. = 6 ft. ![]() dact.). Fractions of a dactyl would be almost unavoidable if the entasis of a column were set out by means of co-ordinates, as it apparently was at Didyma, but Bundgaard, J., Mnesicles (1957), 137–8Google Scholar, has suggested that a springy piece of wood was normally used to give the required curve. Such a method could well have been considered impracticable with the 19·7-m.-high columns of the temple at Didyma, so that the use of co-ordinates was perhaps exceptional.
dact.). Fractions of a dactyl would be almost unavoidable if the entasis of a column were set out by means of co-ordinates, as it apparently was at Didyma, but Bundgaard, J., Mnesicles (1957), 137–8Google Scholar, has suggested that a springy piece of wood was normally used to give the required curve. Such a method could well have been considered impracticable with the 19·7-m.-high columns of the temple at Didyma, so that the use of co-ordinates was perhaps exceptional.
166 This does not imply, of course, that they worked only to the nearest dactyl; cf. pp. 95–7 below.
167 The occurrence in IG vii. 3073. 115 of ![]() (= ‘about a dactyl’ rather than ‘a small dactyl’; cf. Buck, C. D., Petersen, W., A Reverse Index of Greek Nouns and Adjectives (1945) 637–8)Google Scholar suggests that small fractions of a dactyl were not normally measured, for one would otherwise expect a more precise expression.
(= ‘about a dactyl’ rather than ‘a small dactyl’; cf. Buck, C. D., Petersen, W., A Reverse Index of Greek Nouns and Adjectives (1945) 637–8)Google Scholar suggests that small fractions of a dactyl were not normally measured, for one would otherwise expect a more precise expression.
168 Both callipers and dividers are shown on Roman reliefs (Orlandos ii. figs. 73–4).
169 For the diabetes as a levelling instrument see Orlandosii. 135–7.
170 See Orlandos i. 29 n. 1, ii. 268 n. 3.
171 BSA fix (1964) 101. Notice how once this error had occurred, its effect was felt right up the building, with triglyphs of different sizes required for the north and east colonnades (ibid. 108–9).
172 Humann, C., Magnesia am Maeander (1904) 107.Google Scholar