Hostname: page-component-8448b6f56d-c47g7 Total loading time: 0 Render date: 2024-04-24T16:23:24.462Z Has data issue: false hasContentIssue false
  • English
  • Français

DISCRETE SYMMETRIES OF LOW-DIMENSIONAL DIRAC MODELS: A SELECTIVE REVIEW WITH A FOCUS ON CONDENSED-MATTER REALIZATIONS

Part of: Groups and algebras in quantum theory

Published online by Cambridge University Press:  19 August 2015

R. WINKLER  and
U. ZÜLICKE
R. WINKLER
Affiliation:
Department of Physics, Northern Illinois University, DeKalb, IL 60115, USA Institut für Theoretische Physik, Universität Regensburg, 93040 Regensburg, Germany email rwinkler@niu.edu
U. ZÜLICKE*
Affiliation:
School of Chemical and Physical Sciences and MacDiarmid Institute for Advanced Materials and Nanotechnology, Victoria University of Wellington, PO Box 600, Wellington 6140, New Zealand email uli.zuelicke@vuw.ac.nz
*
✉uli.zuelicke@vuw.ac.nz
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The most fundamental characteristic of a physical system can often be deduced from its behaviour under discrete symmetry transformations, such as time reversal, parity and chirality. Here, we review some of the basic symmetry properties of the relativistic quantum theories for free electrons in (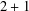$2+1$)- and (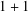$1+1$)-dimensional spacetime. Additional flavour degrees of freedom are necessary to properly define symmetry operations in (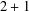$2+1$) dimensions, and are generally present in physical realizations of such systems, for example in single sheets of graphite. We find that there exist two possibilities for defining any flavour-coupling discrete symmetry operation of the two-flavour (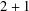$2+1$)-dimensional Dirac theory. Some physical implications of this previously unnoticed duplicity are discussed.

Keywords

relativistic quantum physicsreduced dimensionalityDirac Hamiltoniansquasi-relativity in solids

MSC classification

Primary: 81R05: Finite-dimensional groups and algebras motivated by physics and their representations
Type
Research Article
Information
The ANZIAM Journal , Volume 57 , Issue 1 , July 2015 , pp. 3 - 17
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/3.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© 2015 Australian Mathematical Society

References

Akhmerov, A. R. and Beenakker, C. W. J., “Detection of valley polarization in graphene by a superconducting contact”, Phys. Rev. Lett. 98 (2007) 157003 doi:10.1103/PhysRevLett.98.157003.CrossRefGoogle ScholarPubMed
Aleiner, I. L. and Efetov, K. B., “Effect of disorder on transport in graphene”, Phys. Rev. Lett. 97 (2006) 236801; doi:10.1103/PhysRevLett.97.236801.CrossRefGoogle ScholarPubMed
Altland, A. and Zirnbauer, M. R., “Nonstandard symmetry classes in mesoscopic normal–superconducting hybrid structures”, Phys. Rev. B 55 (1997) 1142–1161 doi:10.1103/PhysRevB.55.1142.CrossRefGoogle Scholar
Appelquist, T. W., Bowick, M., Karabali, D. and Wijewardhana, L. C. R., “Spontaneous chiral-symmetry breaking in three-dimensional QED”, Phys. Rev. D 33 (1986) 3704–3713 doi:10.1103/PhysRevD.33.3704.CrossRefGoogle ScholarPubMed
Beenakker, C. W. J., “Colloquium: Andreev reflection and Klein tunnelling in graphene”, Rev. Mod. Phys. 80 (2008) 1337–1354; doi:10.1103/RevModPhys.80.1337.CrossRefGoogle Scholar
Bernard, D., Kim, E.-A. and LeClair, A., “Edge states for topological insulators in two dimensions and their Luttinger-like liquids”, Phys. Rev. B 86 (2012) 205116 doi:10.1103/PhysRevB.86.205116.CrossRefGoogle Scholar
Bernard, D. and LeClair, A., “A classification of 2D random Dirac fermions”, J. Phys. A: Math. Gen. 35 (2002) 2555–2567; doi:10.1088/0305-4470/35/11/303.CrossRefGoogle Scholar
Bir, G. L. and Pikus, G. E., Symmetry and strain-induced effects in semiconductors (Wiley, New York, 1974).Google Scholar
Castro Neto, A. H., Guinea, F., Peres, N. M. R., Novoselov, K. S. and Geim, A. K., “The electronic properties of graphene”, Rev. Mod. Phys. 81 (2009) 109–162; doi:10.1103/RevModPhys.81.109.CrossRefGoogle Scholar
Chamon, C., Hou, C.-Y., Jackiw, R., Mudry, C., Pi, S.-Y. and Semenoff, G., “Electron fractionalization for two-dimensional Dirac fermions”, Phys. Rev. B 77 (2008) 235431 doi:10.1103/PhysRevB.77.235431.CrossRefGoogle Scholar
Cirac, J. I., Maraner, P. and Pachos, J. K., “Cold atom simulation of interacting relativistic quantum field theories”, Phys. Rev. Lett. 105 (2010) 190403; doi:10.1103/PhysRevLett.105.190403.CrossRefGoogle ScholarPubMed
Dirac, P. A. M., “The quantum theory of the electron”, Proc. R. Soc. Lond. A 117 (1928) 610–624; doi:10.1098/rspa.1928.0023.Google Scholar
Dittrich, W. and Gies, H., Probing the quantum vacuum (Springer, Berlin, 2000) Chapter 4, 155–180.Google Scholar
Geim, A. K., “Graphene: status and prospects”, Science 324 (2009) 1530–1534 doi:10.1126/science.1158877.CrossRefGoogle ScholarPubMed
Gibertini, M., Singha, A., Pellegrini, V., Polini, M., Vignale, G., Pinczuk, A., Pfeiffer, L. N. and West, K. W., “Engineering artificial graphene in a 2D electron gas”, Phys. Rev. B 79 (2009) 241406(R); doi:10.1103/PhysRevB.79.241406.CrossRefGoogle Scholar
Goldman, N., Kubasiak, A., Bermudez, A., Gaspard, P., Lewenstein, M. and Martin-Delgado, M. A., “Non-abelian optical lattices: anomalous quantum Hall effect and Dirac fermions”, Phys. Rev. Lett. 103 (2009) 035301; doi:10.1103/PhysRevLett.103.035301.CrossRefGoogle ScholarPubMed
Gomes, K. K., Mar, W., Ko, W., Guinea, F. and Manoharan, H. C., “Designer Dirac fermions and topological phases in molecular graphene”, Nature 483 (2012) 306–310 doi:10.1038/nature10941.CrossRefGoogle ScholarPubMed
Greiner, W., Relativistic quantum mechanics. Wave equations, 3rd edn (Springer, Berlin, 2000).CrossRefGoogle Scholar
Gusynin, V. P., Sharapov, S. G. and Carbotte, J. P., “AC conductivity of graphene: from tight-binding model to $2+1$-dimensional quantum electrodynamics”, Int. J. Mod. Phys. B 21 (2007) 4611–4658; doi:10.1142/S0217979207038022.CrossRefGoogle Scholar
Haldane, F. D. M. and Raghu, S., “Possible realization of directional optical waveguides in photonic crystals with broken time-reversal symmetry”, Phys. Rev. Lett. 100 (2008) 013904 doi:10.1103/PhysRevLett.100.013904.CrossRefGoogle ScholarPubMed
Jackiw, R. and Templeton, S., “How super-renormalizable interactions cure their infrared divergences”, Phys. Rev. D 23 (1981) 2291–2304; doi:10.1103/PhysRevD.23.2291.CrossRefGoogle Scholar
Kitaev, A., “Periodic table for topological insulators and superconductors”, AIP Conf. Proc. 1134 (2009) 22–30; doi:10.1063/1.3149495.CrossRefGoogle Scholar
Kosiński, P., Maślanka, P., Sławińska, J. and Zasada, I., “$\text{QED}_{2+1}$ in graphene: symmetries of Dirac equation in $2+1$ dimensions”, Prog. Theor. Phys. 128 (2012) 727–739; doi:10.1143/PTP.128.727.CrossRefGoogle Scholar
Leutwyler, H. and Smilga, A., “Spectrum of Dirac operator and role of winding number in QCD”, Phys. Rev. D 46 (1992) 5607–5632; doi:10.1103/PhysRevD.46.5607.CrossRefGoogle ScholarPubMed
McCann, E., Kechedzhi, K., Fal’ko, V. I., Suzuura, H., Ando, T. and Altshuler, B. L., “Weak-localization magnetoresistance and valley symmetry in graphene”, Phys. Rev. Lett. 97 (2006) 146805; doi:10.1103/PhysRevLett.97.146805.CrossRefGoogle ScholarPubMed
Ostrovsky, P. M., Gornyi, I. V. and Mirlin, A. D., “Electron transport in disordered graphene”, Phys. Rev. B 74 (2006) 235443; doi:10.1103/PhysRevB.74.235443.CrossRefGoogle Scholar
Park, C.-H. and Louie, S. G., “Making massless Dirac fermions from a patterned two-dimensional electron gas”, Nano Lett. 9 (2009) 1793–1797; doi:10.1021/nl803706c.CrossRefGoogle ScholarPubMed
Qi, X.-L. and Zhang, S.-C., “Topological insulators and superconductors”, Rev. Mod. Phys. 83 (2011) 1057–1110; doi:10.1103/RevModPhys.83.1057.CrossRefGoogle Scholar
Rössler, U., Solid state theory: an introduction, 2nd edn (Springer, Berlin, 2009).CrossRefGoogle Scholar
Ryu, S., Schnyder, A. P., Furusaki, A. and Ludwig, A. W. W., “Topological insulators and superconductors: tenfold way and dimensional hierarchy”, New J. Phys. 12 (2010) 065010; doi:10.1088/1367-2630/12/6/065010.CrossRefGoogle Scholar
Sachs, R. G., The physics of time reversal (University of Chicago Press, Chicago, 1987).Google Scholar
Sakurai, J. J., Advanced quantum mechanics (Addison-Wesley, Reading, MA, 1967).Google Scholar
Sakurai, J. J., Modern quantum mechanics, revised edn (Addison-Wesley, Reading, MA, 1994).Google Scholar
Schnyder, A. P., Ryu, S., Furusaki, A. and Ludwig, A. W. W., “Classification of topological insulators and superconductors in three spatial dimensions”, Phys. Rev. B 78 (2008) 195125 doi:10.1103/PhysRevB.78.195125.CrossRefGoogle Scholar
Semenoff, G. W., “Condensed-matter simulation of a three-dimensional anomaly”, Phys. Rev. Lett. 53 (1984) 2449–2452; doi:10.1103/PhysRevLett.53.2449.CrossRefGoogle Scholar
Sepkhanov, R. A., Nilsson, J. and Beenakker, C. W. J., “Proposed method for detection of the pseudospin-$\frac{1}{2}$ Berry phase in a photonic crystal with a Dirac spectrum”, Phys. Rev. B 78 (2008) 045122; doi:10.1103/PhysRevB.78.045122.CrossRefGoogle Scholar
Singha, A., Gibertini, M., Karmakar, B., Yuan, S., Polini, M., Vignale, G., Katsnelson, M. I., Pinczuk, A., Pfeiffer, L. N., West, K. W. and Pellegrini, V., “Two-dimensional Mott–Hubbard electrons in an artificial honeycomb lattice”, Science 332 (2011) 1176–1179; doi:10.1126/science.1204333.CrossRefGoogle Scholar
Tarruell, L., Greif, D., Uehlinger, T., Jotzu, G. and Esslinger, T., “Creating, moving and merging Dirac points with a Fermi gas in a tunable honeycomb lattice”, Nature 483 (2012) 302–305 doi:10.1038/nature10871.CrossRefGoogle Scholar
Thaller, B., The Dirac equation (Springer, Berlin, 1992).CrossRefGoogle Scholar
Wigner, E. P., Group theory and its application to the quantum mechanics of atomic spectra (Academic Press, New York, 1959).Google Scholar
Winkler, R. and Zülicke, U., “Invariant expansion for the trigonal band structure of graphene”, Phys. Rev. B 82 (2010) 245313; doi:10.1103/PhysRevB.82.245313.CrossRefGoogle Scholar
Winkler, R. and Zülicke, U., “Time reversal of pseudo-spin 1/2 degrees of freedom”, Phys. Lett. A 374 (2010) 4003–4006; doi:10.1016/j.physleta.2010.08.008.CrossRefGoogle Scholar
Wunsch, B., Guinea, F. and Sols, F., “Dirac-point engineering and topological phase transitions in honeycomb optical lattices”, New J. Phys. 10 (2008) 103027 doi:10.1088/1367-2630/10/10/103027.CrossRefGoogle Scholar
Wurm, J., Rycerz, A., Adagideli, I., Wimmer, M., Richter, K. and Baranger, H. U., “Symmetry classes in graphene quantum dots: universal spectral statistics, weak localization, and conductance fluctuations”, Phys. Rev. Lett. 102 (2009) 056806; doi:10.1103/PhysRevLett.102.056806.CrossRefGoogle ScholarPubMed
Wurm, J., Wimmer, M. and Richter, K., “Symmetries and the conductance of graphene nanoribbons with long-range disorder”, Phys. Rev. B 85 (2012) 245418; doi:10.1103/PhysRevB.85.245418.CrossRefGoogle Scholar
Zhu, S.-L., Wang, B. and Duan, L.-M., “Simulation and detection of Dirac fermions with cold atoms in an optical lattice”, Phys. Rev. Lett. 98 (2007) 260402; doi:10.1103/PhysRevLett.98.260402.CrossRefGoogle Scholar
Zirnbauer, M. R., “Riemannian symmetric superspaces and their origin in random-matrix theory”, J. Math. Phys. 37 (1996) 4986–5018; doi:10.1063/1.531675.CrossRefGoogle Scholar