Article contents
EXACT ANALYTICAL EXPRESSIONS FOR THE FINAL EPIDEMIC SIZE OF AN SIR MODEL ON SMALL NETWORKS
Published online by Cambridge University Press: 23 May 2016
Abstract
We investigate the dynamics of a susceptible infected recovered (SIR) epidemic model on small networks with different topologies, as a stepping stone to determining how the structure of a contact network impacts the transmission of infection through a population. For an SIR model on a network of 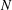 $N$ nodes, there are
$N$ nodes, there are 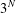 $3^{N}$ configurations that the network can be in. To simplify the analysis, we group the states together based on the number of nodes in each infection state and the symmetries of the network. We derive analytical expressions for the final epidemic size of an SIR model on small networks composed of three or four nodes with different topological structures. Differential equations which describe the transition of the network between states are also derived and solved numerically to confirm our analysis. A stochastic SIR model is numerically simulated on each of the small networks with the same initial conditions and infection parameters to confirm our results independently. We show that the structure of the network, degree of the initial infectious node, number of initial infectious nodes and the transmission rate all significantly impact the final epidemic size of an SIR model on small networks.
$3^{N}$ configurations that the network can be in. To simplify the analysis, we group the states together based on the number of nodes in each infection state and the symmetries of the network. We derive analytical expressions for the final epidemic size of an SIR model on small networks composed of three or four nodes with different topological structures. Differential equations which describe the transition of the network between states are also derived and solved numerically to confirm our analysis. A stochastic SIR model is numerically simulated on each of the small networks with the same initial conditions and infection parameters to confirm our results independently. We show that the structure of the network, degree of the initial infectious node, number of initial infectious nodes and the transmission rate all significantly impact the final epidemic size of an SIR model on small networks.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- © 2016 Australian Mathematical Society
References
- 6
- Cited by

