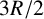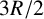1 Introduction
Miscible, density-dependent flow in porous media is important in many engineering fields, such as groundwater contamination remediation, petroleum extraction and sea water intrusion [Reference Al-Dousari, Garrouch and Guedouar2, Reference Holm15, Reference Koch and Zhang17, Reference Nick, Schotting, Gutierrez-Neri and Johannsen18, Reference Quintard, Bertin and Prouvost22, Reference Tran, Bajracharya and Barry26, Reference Watson and Barry29, Reference Zhang and Hocking34–Reference Zhang, Hocking and Seymour36]. Laboratory-scale column experiments are commonly carried out to obtain estimates of the properties of the soil and the transport parameters that characterize contaminant migration through it. Probably, the most straightforward way to perform experiments on nonreactive solute transport in laboratory columns is to first establish a steady-state flow of water through the column, then to switch the influent to a solution with a known chemical composition, leaving the flow rate unchanged (see, for example, [Reference Boon, Bijeljic, Niu and Krevor9, Reference Yong, Mohamed and Warkentin33]). The effluent can be sampled to measure the concentration or visualized with an X-ray medical CT-scanner, and the data obtained can used in conjunction with a model to provide estimates of soil and transport parameters [Reference Bajracharya and Barry3]. This experimental design allows the use of one-dimensional or two-dimensional solute transport models [Reference Bajracharya, Tran and Barry4, Reference Barry6, Reference Chen, Liu, Liang, Liu and Lin10, Reference Kanwar, Johnson and Kirkham16, Reference Overman, Chu and Le20, Reference Rao, Rolston, Jessup and Davidson23, Reference Tran, Bajracharya and Barry26, Reference Tran, Barry and Bajracharya27, Reference Wissmeier, Barry and Phillips32], which simplifies the analysis considerably.
A key parameter is the dispersivity of the solute(s) under consideration. If a one-dimensional solute transport model is used, then the water flow is assumed to be spatially and temporally uniform. For flow through an unconsolidated porous medium, the relationship between flow rate and dispersivity is well known for nonreactive solutes [Reference Bear8, Reference Pfannkuch21]. However, any additional dispersion caused by the apparatus is not included in these estimates. Apparatus-induced dispersion can arise if components of the apparatus cause additional mixing and spreading of the solute front, particularly at the ends of the column apparatus. Apparatus-induced dispersion can also arise if the column apparatus causes nonuniform flow to develop within the column, even when the test soil is homogeneous and uniformly packed.
It is common in column experiments for flow to enter and leave the column through a hole much smaller than the column itself. This occurs for a simple practical reason: the influent or effluent flow occurs in tubes with diameters much less than the soil column diameter. This case was analysed by Barry [Reference Barry6], who developed a general analytical solution for steady flow in such a column, subject to arbitrary head or flux boundary conditions. Although the results of [Reference Barry6] are useful for the analysis of nonuniform flow in a column, they do not consider (i) the effect of variable density flow or (ii) the impact of the flow field on solute dispersion within the column. The purpose of this paper is to quantify both of these aspects of solute transport in soil column experiments.
In the present study, the problem is investigated numerically using a finite-element modelling package, COMSOL Multiphysics [11], which has been employed to solve various partial differential equations in engineering fields [Reference Al-Ali, Hocking, Farrow and Zhang1, Reference Barletta, Zanchini, Lazzari and Terenzi5, Reference Cristea, Bagiu and Agachi12, Reference Sahu and Bhattacharyay24, Reference Wissmeier and Barry31]. The impacts of the dimensions of the apparatus and the soil properties on the dispersion of density-dependent solute transport in porous media are analysed numerically.
2 Problem formulation
2.1 Governing equations
We consider a typical experiment carried out in cylindrical soil columns [Reference Watson, Barry, Schotting and Hassanizadeh30] containing uniformly packed isotropic soil, with influent and effluent orifices aligned along the column centreline. Such experiments produce axisymmetric flow in a cylinder containing soil with porosity n and intrinsic permeability
![]() $\kappa $
, as shown in Figure 1. The column radius is R, with height is H and outlet orifice radius is
$\kappa $
, as shown in Figure 1. The column radius is R, with height is H and outlet orifice radius is
![]() $r_n$
. The origin of the cylindrical coordinate system is located at the centre of the bottom of the column
$r_n$
. The origin of the cylindrical coordinate system is located at the centre of the bottom of the column
![]() $( r,z ) =( 0,0 )$
. The transported fluid has density
$( r,z ) =( 0,0 )$
. The transported fluid has density
![]() $\rho $
, dynamic viscosity
$\rho $
, dynamic viscosity
![]() $\mu $
and salt mass fraction
$\mu $
and salt mass fraction
![]() $\omega $
.
$\omega $
.
The flow and the solute satisfy Darcy’s law and the mass conservation equations, which are summarized as follows. (See [Reference Watson, Barry, Schotting and Hassanizadeh30].)
Darcy’s law and Fick’s law
 $$ \begin{align} &\mathbf{J}=-\rho \boldsymbol{D}\cdot \nabla \omega, \nonumber \\ &\text{where }\mathbf{D}=( D_{ij} ) =\bigg( n( D_m+\alpha _T| \boldsymbol{q} | ) \delta _{ij}+n( \alpha _L-\alpha _T ) \frac{q_iq_j}{| \boldsymbol{q} |} \bigg),\quad i=1, 2, 3. \end{align} $$
$$ \begin{align} &\mathbf{J}=-\rho \boldsymbol{D}\cdot \nabla \omega, \nonumber \\ &\text{where }\mathbf{D}=( D_{ij} ) =\bigg( n( D_m+\alpha _T| \boldsymbol{q} | ) \delta _{ij}+n( \alpha _L-\alpha _T ) \frac{q_iq_j}{| \boldsymbol{q} |} \bigg),\quad i=1, 2, 3. \end{align} $$
Here,
![]() $\mathbf {q}$
denotes the specific discharge, p is the fluid pressure,
$\mathbf {q}$
denotes the specific discharge, p is the fluid pressure,
![]() $\mathbf {g}=(0,0,g)$
is the gravitational acceleration, n is the porosity,
$\mathbf {g}=(0,0,g)$
is the gravitational acceleration, n is the porosity,
![]() $\mathbf {h}$
is the dispersive mass flux and
$\mathbf {h}$
is the dispersive mass flux and
![]() $\mathbf {D}=(D_{ij})$
the hydrodynamic dispersion tensor [Reference Bear8], where
$\mathbf {D}=(D_{ij})$
the hydrodynamic dispersion tensor [Reference Bear8], where
![]() $D_m$
is the mass diffusivity and
$D_m$
is the mass diffusivity and
![]() $\alpha _L$
and
$\alpha _L$
and
![]() $\alpha _T$
are the longitudinal and transversal dispersivity, respectively.
$\alpha _T$
are the longitudinal and transversal dispersivity, respectively.

Figure 1 Two different soil column study configuration diagrams: (a) experimental set-up of Watson et al. [Reference Watson, Barry, Schotting and Hassanizadeh30]; and (b) set-up of the flow convergence study by Barry [Reference Barry6].
Conservation of mass of the water and solute
where
![]() $\rho $
is the fluid density,
$\rho $
is the fluid density,
![]() $\mu $
is the dynamic viscosity of fluid and
$\mu $
is the dynamic viscosity of fluid and
![]() $\omega $
is the fractional solute concentration. The saltwater density and viscosity, respectively, are given by,
$\omega $
is the fractional solute concentration. The saltwater density and viscosity, respectively, are given by,
In the equations of state (2.5) and (2.6) for brine, the constant
![]() $\gamma = 0.6923$
[Reference Hassanizadeh and Leijnse14], while, for the freshwater reference state,
$\gamma = 0.6923$
[Reference Hassanizadeh and Leijnse14], while, for the freshwater reference state,
![]() $\rho _0 = 998.23$
kg/m
$\rho _0 = 998.23$
kg/m
![]() $^3$
and
$^3$
and
![]() $\mu _0 = 0.001 \ \mathrm {N_S}$
/m
$\mu _0 = 0.001 \ \mathrm {N_S}$
/m
![]() $^2$
at 20
$^2$
at 20
![]() $^{\circ }$
C and 1 atm.
$^{\circ }$
C and 1 atm.
The full set of equations is coupled between density
![]() $\rho $
, viscosity
$\rho $
, viscosity
![]() $\mu $
, specific discharge
$\mu $
, specific discharge
![]() $\mathbf {q}$
and dispersive flux
$\mathbf {q}$
and dispersive flux
![]() $\mathbf {J}$
. All variables with dimensions of length are scaled with R, the radius of the column, so that
$\mathbf {J}$
. All variables with dimensions of length are scaled with R, the radius of the column, so that
The other nondimensional variables are
The reference hydraulic conductivity,
![]() $K=\kappa \rho _0g/\mu _0$
with
$K=\kappa \rho _0g/\mu _0$
with
![]() $\kappa $
as the permeability, is used to scale time
$\kappa $
as the permeability, is used to scale time
![]() $t^*=tK/nR$
, the discharge flux
$t^*=tK/nR$
, the discharge flux
![]() $\mathbf {q}^*=\mathbf {q}/q_{in}$
, the hydrodynamic dispersion tensor
$\mathbf {q}^*=\mathbf {q}/q_{in}$
, the hydrodynamic dispersion tensor
![]() $\boldsymbol {D}^*=\boldsymbol {D}/Rq_{in}$
and the dispersive mass flux
$\boldsymbol {D}^*=\boldsymbol {D}/Rq_{in}$
and the dispersive mass flux
![]() $\mathbf {J}^*=\mathbf {J}/\rho _0Rq_{in}$
, where
$\mathbf {J}^*=\mathbf {J}/\rho _0Rq_{in}$
, where
![]() $q_{in}$
is the discharge flux for
$q_{in}$
is the discharge flux for
![]() $0<r<R\text { and }z=0$
. Then equations (2.1)–(2.6) can be rewritten as follows.
$0<r<R\text { and }z=0$
. Then equations (2.1)–(2.6) can be rewritten as follows.
Darcy’s law and Fick’s law
 $$ \begin{align} \mathbf{q}^*&=-\frac{K}{q_{in}}\frac{1}{\mu ^*}( \nabla p^*+\rho ^*\mathbf{g}^* ), \end{align} $$
$$ \begin{align} \mathbf{q}^*&=-\frac{K}{q_{in}}\frac{1}{\mu ^*}( \nabla p^*+\rho ^*\mathbf{g}^* ), \end{align} $$
Conservation of mass
with
The solute transport depends on the flow, as the velocity
![]() $\mathbf {q}^*$
determines both advective and dispersive transport. The density
$\mathbf {q}^*$
determines both advective and dispersive transport. The density
![]() $\rho ^*( \omega )$
and viscosity
$\rho ^*( \omega )$
and viscosity
![]() $\mu ^*( \omega )$
of the solution are coupled back to the flow equation through their dependencies on the mass fraction of the solution, which produces two nonlinear diffusive partial differential equations for the variables
$\mu ^*( \omega )$
of the solution are coupled back to the flow equation through their dependencies on the mass fraction of the solution, which produces two nonlinear diffusive partial differential equations for the variables
![]() $\omega $
and
$\omega $
and
![]() $p^*$
as functions of
$p^*$
as functions of
![]() $z*$
,
$z*$
,
![]() $r^*$
and
$r^*$
and
![]() $t^*$
.
$t^*$
.
2.2 Initial and boundary conditions
Following the experiment set-up of [Reference Watson and Barry29], it is assumed that the fluid enters the column from the bottom and exits from the orifice at the top. The initial conditions for the simulations are that the fluid in the column is under hydrostatic condition and there is no solute, so that
 $$ \begin{align} \begin{cases} p^*=z^*\\ \omega ^*=0\\ \end{cases} \text{for } t^*=0, 0\leq z^*\leq H^*\text{ and } 0\leq r^*\leq 1. \end{align} $$
$$ \begin{align} \begin{cases} p^*=z^*\\ \omega ^*=0\\ \end{cases} \text{for } t^*=0, 0\leq z^*\leq H^*\text{ and } 0\leq r^*\leq 1. \end{align} $$
Measured flow rate data at the influent boundary and measured pressure data at the effluent boundary are used for the boundary conditions applied to the fluid mass balance matrix equation for comparison with the experiment results. At the inlet, a first-type of concentration-type input boundary condition (see, for example, [Reference Barry and Sposito7, Reference Van Genuchten and Parker28]) was used, where the measured flow rates
![]() $q^*_{in}$
and solute concentration
$q^*_{in}$
and solute concentration
![]() $\omega _{in}$
are specified: that is,
$\omega _{in}$
are specified: that is,
At the orifice, the most realistic assumption for the finite column apparatus is the Danckwerts boundary condition [Reference Danckwerts13, Reference Schwartz, McInnes, Juo, Wilding and Reddell25, Reference Van Genuchten and Parker28] for the solute concentration and constant pressure for the fluid: that is,
In the present study, COMSOL Multiphysics modules of Darcy’s law and solute transport are coupled for a numerical study on the above apparatus-induced dispersion in porous media.
3 Simulations and analysis
3.1 Convergent flow
The problem described above produces a two-dimensional axisymmetric flow regime. When the outlet radius is much less than the column radius, that is,
![]() $r_n\leq R$
, the convergent flow forms near the outlet zone. The solute dispersion coefficient depends on the flow rate, that is, the apparatus-induced dispersion in laboratory apparatus is caused by the nonuniform fluid.
$r_n\leq R$
, the convergent flow forms near the outlet zone. The solute dispersion coefficient depends on the flow rate, that is, the apparatus-induced dispersion in laboratory apparatus is caused by the nonuniform fluid.
Barry [Reference Barry6] developed an analytical solution for the steady-state case with a constant
![]() $\rho _*$
and
$\rho _*$
and
 $$ \begin{align*} \omega = 0, \quad \frac{\partial ^2\phi ^*}{{\partial z^*}^2}+\frac{1}{r^*}\frac{\partial}{\partial r^*}\bigg( r^*\frac{\partial \phi ^*}{\partial r^*} \bigg) =0,\end{align*} $$
$$ \begin{align*} \omega = 0, \quad \frac{\partial ^2\phi ^*}{{\partial z^*}^2}+\frac{1}{r^*}\frac{\partial}{\partial r^*}\bigg( r^*\frac{\partial \phi ^*}{\partial r^*} \bigg) =0,\end{align*} $$
where
![]() $\phi $
is the hydraulic head,
$\phi $
is the hydraulic head,
![]() $q_{r}^{*}=-K(\partial \phi ^*/\partial r^*)$
and
$q_{r}^{*}=-K(\partial \phi ^*/\partial r^*)$
and
![]() $q_{z}^{*}=-K(\partial \phi ^*/\partial z^*)$
. The orientation of the soil column is reversed, as shown in Figure 1, where the flow comes in from the top and exits from the orifice at the bottom. The boundary conditions at
$q_{z}^{*}=-K(\partial \phi ^*/\partial z^*)$
. The orientation of the soil column is reversed, as shown in Figure 1, where the flow comes in from the top and exits from the orifice at the bottom. The boundary conditions at
![]() $z^*=0$
are [Reference Barry6]
$z^*=0$
are [Reference Barry6]
 $$ \begin{align} \frac{\partial \phi ^*}{\partial z^*}=\bigg( \frac{R^*}{r_{n}^{*}} \bigg) ^2\quad\text{for } 0\le r^*<r_{n}^{*}\quad \text{and} \quad \frac{\partial \phi ^*}{\partial z^*}=0\quad\text{for }r_{n}^{*}\le r^*<1. \end{align} $$
$$ \begin{align} \frac{\partial \phi ^*}{\partial z^*}=\bigg( \frac{R^*}{r_{n}^{*}} \bigg) ^2\quad\text{for } 0\le r^*<r_{n}^{*}\quad \text{and} \quad \frac{\partial \phi ^*}{\partial z^*}=0\quad\text{for }r_{n}^{*}\le r^*<1. \end{align} $$
The analytical solutions for the case where fluid exits the column through an orifice with a radius less than the column radius, that is,
![]() ${r_n}^*$
= 0.01, 0.25, 0.5 and 0.75, and with no variability in the head condition at the column entry, are compared with the present numerical results. For the comparison, the parameters used in the simulations include
${r_n}^*$
= 0.01, 0.25, 0.5 and 0.75, and with no variability in the head condition at the column entry, are compared with the present numerical results. For the comparison, the parameters used in the simulations include
![]() $H^*=2$
,
$H^*=2$
,
![]() $R^*=1$
and
$R^*=1$
and
![]() $\phi ^* (z^*=H^* )=20$
, which are consistent with those in [Reference Barry6]. The nonuniformities introduced by the orifice radius of the typical soil column in Figure 1(b) are further investigated for the boundary conditions of
$\phi ^* (z^*=H^* )=20$
, which are consistent with those in [Reference Barry6]. The nonuniformities introduced by the orifice radius of the typical soil column in Figure 1(b) are further investigated for the boundary conditions of
![]() $p^*=0$
at
$p^*=0$
at
![]() $z^*=H^*$
and
$z^*=H^*$
and
![]() $q^*={q_{in}}^*=1$
at
$q^*={q_{in}}^*=1$
at
![]() $z^*=0$
. To determine the converging flow zone, both the radial flux
$z^*=0$
. To determine the converging flow zone, both the radial flux
![]() $q_r^*$
and the longitudinal flux
$q_r^*$
and the longitudinal flux
![]() $q_z^*$
are examined. For an ideal uniform flow in a column, the steady discharge rate is
$q_z^*$
are examined. For an ideal uniform flow in a column, the steady discharge rate is
![]() $\mathbf {q}^*=( 0, q_{in}^{*} )$
. The disturbance to
$\mathbf {q}^*=( 0, q_{in}^{*} )$
. The disturbance to
![]() $\mathbf {q}^*$
is defined as
$\mathbf {q}^*$
is defined as
![]() $\Delta \mathbf {q}^*=( \Delta q_{r}^{*},\Delta q_{z}^{*} )$
, where
$\Delta \mathbf {q}^*=( \Delta q_{r}^{*},\Delta q_{z}^{*} )$
, where
![]() $\Delta q_{r}^{*}=| q_{r}^{*}-0 |\text { and }\Delta q_{z}^{*}=| q_{z}^{*}-q_{in}^{*} |$
. Following [Reference Barry6], we define the disturbed region of fluid as that in which
$\Delta q_{r}^{*}=| q_{r}^{*}-0 |\text { and }\Delta q_{z}^{*}=| q_{z}^{*}-q_{in}^{*} |$
. Following [Reference Barry6], we define the disturbed region of fluid as that in which
![]() $| \Delta \mathbf {q}^* |>0.02q_{in}^{*}$
, and the dissipation height of the orifice disturbance is defined as the maximum vertical height
$| \Delta \mathbf {q}^* |>0.02q_{in}^{*}$
, and the dissipation height of the orifice disturbance is defined as the maximum vertical height
![]() $d^*$
between the centre of the orifice and the location where
$d^*$
between the centre of the orifice and the location where
![]() $| \Delta \mathbf {q}^*\text {(}r^*=0) |=0.02q_{in}^{*}$
. The disturbance factor 0.02 was selected to be consistent with that used by Barry [Reference Barry6].
$| \Delta \mathbf {q}^*\text {(}r^*=0) |=0.02q_{in}^{*}$
. The disturbance factor 0.02 was selected to be consistent with that used by Barry [Reference Barry6].
To identify the impact of the orifice on the flow pattern in the column, the flow distributions for
![]() ${r_n}^*$
= 0.1, 0.25, 0.5 and 0.75 were simulated and presented in Figure 2. The vectors present the discharge rates and directions, the approximately horizontal black contour lines are hydraulic head and the black lines parallel to discharge rate vectors are streamlines. The red-cross lines represent where
${r_n}^*$
= 0.1, 0.25, 0.5 and 0.75 were simulated and presented in Figure 2. The vectors present the discharge rates and directions, the approximately horizontal black contour lines are hydraulic head and the black lines parallel to discharge rate vectors are streamlines. The red-cross lines represent where
![]() $| \Delta \mathbf {q}^* |=0.02q_{in}^{*}$
, and the domain under it is the disturbed zone, that is,
$| \Delta \mathbf {q}^* |=0.02q_{in}^{*}$
, and the domain under it is the disturbed zone, that is,
![]() $| \Delta \mathbf {q}^* |>0.02q_{in}^{*}$
. It can be seen that the dissipation height
$| \Delta \mathbf {q}^* |>0.02q_{in}^{*}$
. It can be seen that the dissipation height
![]() $d^*$
is larger for a smaller orifice radius, that is, there is a larger converging flow zone. The nonuniform domain size increases when
$d^*$
is larger for a smaller orifice radius, that is, there is a larger converging flow zone. The nonuniform domain size increases when
![]() ${r_n}^*$
decreases. When
${r_n}^*$
decreases. When
![]() $r_{n}^{*}\rightarrow 0.1$
,
$r_{n}^{*}\rightarrow 0.1$
,
![]() $d^*\rightarrow 3/2$
. On the other hand, when
$d^*\rightarrow 3/2$
. On the other hand, when
![]() $r_{n}^{*}\rightarrow R$
, no converging flow zone exists, that is, the flow in the column is uniform. These results are in a good agreement with the analytical solution in [Reference Barry6], which provides some supporting evidence that COMSOL Multiphysics is a valid numerical tool for the study of Darcy flows.
$r_{n}^{*}\rightarrow R$
, no converging flow zone exists, that is, the flow in the column is uniform. These results are in a good agreement with the analytical solution in [Reference Barry6], which provides some supporting evidence that COMSOL Multiphysics is a valid numerical tool for the study of Darcy flows.

Figure 2 Steady flow for
![]() $H^*=2$
,
$H^*=2$
,
![]() $R^*=1$
and various orifice radii: (a)
$R^*=1$
and various orifice radii: (a)
![]() ${r_n}^* = 0.1$
; (b)
${r_n}^* = 0.1$
; (b)
![]() ${r_n}^* =0.25$
; (c)
${r_n}^* =0.25$
; (c)
![]() ${r_n}^* = 0.5$
; and (d)
${r_n}^* = 0.5$
; and (d)
![]() ${r_n}^* = 0.75$
. The vectors present the discharge rates and directions, the approximately horizontal black contour lines are hydraulic head and the black lines parallel to discharge rate vectors are streamlines. The red-cross lines represent where
${r_n}^* = 0.75$
. The vectors present the discharge rates and directions, the approximately horizontal black contour lines are hydraulic head and the black lines parallel to discharge rate vectors are streamlines. The red-cross lines represent where
![]() $| \Delta \mathbf {q}^* |=0.02q_{in}^{*}$
, the domain under it is the disturbed zone, that is,
$| \Delta \mathbf {q}^* |=0.02q_{in}^{*}$
, the domain under it is the disturbed zone, that is,
![]() $| \Delta \mathbf {q}^* |>0.02q_{in}^{*}$
.
$| \Delta \mathbf {q}^* |>0.02q_{in}^{*}$
.

Figure 3 Steady flow for
![]() ${r_n}^*=0.1$
,
${r_n}^*=0.1$
,
![]() ${R}^*=0.1$
: (a)
${R}^*=0.1$
: (a)
![]() ${H}^*=4$
; and (b)
${H}^*=4$
; and (b)
![]() ${H}^*=2$
.
${H}^*=2$
.
The impact of the soil column height on the nonuniform flow was also examined. For the orifice radius
![]() ${r_n}^*=0.1$
, the same boundary conditions were used, but column heights of
${r_n}^*=0.1$
, the same boundary conditions were used, but column heights of
![]() $H^*=2$
and 4 are simulated. Figure 3 shows the flow distributions in the converging zones. It can be seen that the disturbance height
$H^*=2$
and 4 are simulated. Figure 3 shows the flow distributions in the converging zones. It can be seen that the disturbance height
![]() $d^*\approx 1.50$
for both cases, and when
$d^*\approx 1.50$
for both cases, and when
![]() $z^*>3/2$
in the column, the flow is always uniform. The disturbance distance due to the orifice is summarized in Figure 5. This confirms that the maximum dissipation length scale is less than
$z^*>3/2$
in the column, the flow is always uniform. The disturbance distance due to the orifice is summarized in Figure 5. This confirms that the maximum dissipation length scale is less than
![]() $3/2$
of the column radius. Therefore, once the column dimension and the orifice size are known, the converging zone height can be determined, which is a useful reference for the design of laboratory transport experiments.
$3/2$
of the column radius. Therefore, once the column dimension and the orifice size are known, the converging zone height can be determined, which is a useful reference for the design of laboratory transport experiments.
The apparatus-induced dispersion occurs mainly in this converging zone. In other words, outside the convergent flow zone, solute breakthrough curves measured in-situ can be used to obtain accurate soil parameter estimates.
3.2 Solute transport model
The magnitude of the hydrodynamic dispersion results from external forces acting on the liquid and variation in liquid properties, such as density and viscosity. Consider a solute transported in a saturated, uniform flow through a porous medium in a column, as in Figure 1(a) (that is,
![]() ${r_n}^*=R^*=1$
). In [Reference Ogata and Banks19] an analytical solution was developed that described the advection-dispersion transport for uniform flow, that is, the solution of equations (2.7)–(2.12) for a constant
${r_n}^*=R^*=1$
). In [Reference Ogata and Banks19] an analytical solution was developed that described the advection-dispersion transport for uniform flow, that is, the solution of equations (2.7)–(2.12) for a constant
![]() $\rho ^*$
and
$\rho ^*$
and
![]() $R^*/H^*\leq 1$
, (or infinite
$R^*/H^*\leq 1$
, (or infinite
![]() $H^*$
), as
$H^*$
), as
 $$ \begin{align} \omega (z,t)=\frac{\omega _{in}}{2}\bigg[ \mathrm{erfc}\bigg( \frac{z^*-q_{z}^{*}t^*}{\sqrt{4D_{z}^{*}t^*}} \bigg) +\exp \!\:\bigg( \frac{q_{z}^{*}z^*}{D_{z}^{*}} \bigg) \mathrm{erfc}\bigg( \frac{z^*+q_{z}^{*}t^*}{\sqrt{4D_{z}^{*}t^*}} \bigg) \bigg], \end{align} $$
$$ \begin{align} \omega (z,t)=\frac{\omega _{in}}{2}\bigg[ \mathrm{erfc}\bigg( \frac{z^*-q_{z}^{*}t^*}{\sqrt{4D_{z}^{*}t^*}} \bigg) +\exp \!\:\bigg( \frac{q_{z}^{*}z^*}{D_{z}^{*}} \bigg) \mathrm{erfc}\bigg( \frac{z^*+q_{z}^{*}t^*}{\sqrt{4D_{z}^{*}t^*}} \bigg) \bigg], \end{align} $$
where
![]() ${D_z}^*$
is the longitudinal dispersion coefficient. Substituting equation (2.15) into the solute dispersion equation (2.8), gives the longitudinal dispersive flux
${D_z}^*$
is the longitudinal dispersion coefficient. Substituting equation (2.15) into the solute dispersion equation (2.8), gives the longitudinal dispersive flux
 $$ \begin{align} {J_z}^*(t)=-\rho ^*{D_z}^*\frac{\omega _{in}}{\sqrt{4{\pi D_z}^*t^*}} \begin{cases} -\exp \bigg( \dfrac{(z^*-{q_z}^*t^*)^2}{4{D_z}^*t^*} \bigg) -\exp \bigg( \dfrac{z^*{q_z}^*}{{D_z}^*}-\dfrac{(z^*+{q_z}^*t^*)^2}{4{D_z}^*t^*} \bigg)\\[4pt] +\sqrt{\dfrac{4\pi t^*}{{D_z}^*}}{q_z}^*\exp \bigg( \dfrac{z^*{q_z}^*}{{D_z}^*} \bigg) \mathrm{erfc}\bigg( \dfrac{z^*+{q_z}^*t^*}{\sqrt{4{D_z}^*t^*}} \bigg). \end{cases}\nonumber\\[-16pt] \end{align} $$
$$ \begin{align} {J_z}^*(t)=-\rho ^*{D_z}^*\frac{\omega _{in}}{\sqrt{4{\pi D_z}^*t^*}} \begin{cases} -\exp \bigg( \dfrac{(z^*-{q_z}^*t^*)^2}{4{D_z}^*t^*} \bigg) -\exp \bigg( \dfrac{z^*{q_z}^*}{{D_z}^*}-\dfrac{(z^*+{q_z}^*t^*)^2}{4{D_z}^*t^*} \bigg)\\[4pt] +\sqrt{\dfrac{4\pi t^*}{{D_z}^*}}{q_z}^*\exp \bigg( \dfrac{z^*{q_z}^*}{{D_z}^*} \bigg) \mathrm{erfc}\bigg( \dfrac{z^*+{q_z}^*t^*}{\sqrt{4{D_z}^*t^*}} \bigg). \end{cases}\nonumber\\[-16pt] \end{align} $$
To validate the COMSOL solute transport model, the breakthrough curve (BTC) for uniform flow and its dispersive flux are calculated and compared with those estimated using the analytical solution of equations (3.2) and (3.3) for the parameters in Table 1.
The analytical and numerical results for the BTC for uniform flow and the dispersive flux at
![]() $z^* = 2$
are shown in Figure 4, where reasonably good agreement is evident.
$z^* = 2$
are shown in Figure 4, where reasonably good agreement is evident.
Watson et al. [Reference Watson, Barry, Schotting and Hassanizadeh30] designed laboratory column apparatus for an apparatus-induced dispersion study that consisted of an acrylic column with a detachable base and piston top cap. The data in [Reference Watson, Barry, Schotting and Hassanizadeh30] are also used to verify the COMSOL model for the solute transport in a nonuniform flow. The case CS1-5U in [Reference Watson, Barry, Schotting and Hassanizadeh30] is selected, which has the following parameters in Table 2.
Table 1 Parameters for a uniform flow simulation.


Figure 4 The breakthrough curves, that is, the salt concentration at the exit, for uniform flow are calculated using the analytical and numerical methods.
Table 2 Parameters for Case CS1-5U in [Reference Watson, Barry, Schotting and Hassanizadeh30].


Figure 5 Comparison of the experimental cumulative effluent of solute with the analytical and numerical solutions.
The experimental data for cumulative effluent was compared with the analytical solution using equations (3.2) and (3.3) and the numerical solution (Figure 5). The analytical solution, equation (3.2), derived by Ogata and Banks [Reference Ogata and Banks19] is for a semiinfinite one-dimensional half-space with an imposed uniform flow. It obviously is not able to calculate the nonuniform solute transport accurately, as the additional dispersion caused by the apparatus is not included in these estimates. However, the numerical model provided a relatively accurate estimate of the solute transport, which provides support for the use of COMSOL for studies on apparatus-induced dispersion.
3.3 Apparatus-induced dispersion
When a solute is transported in a nonuniform, density-dependent flow, the displacing solute concentration influences the velocity field. The flow nonuniformity and the density variations will, consequently, affect hydrodynamic dispersion. The transport process is complex. Therefore, the COMSOL model is used to investigate the effects of the apparatus dimensions, the soil parameters and the solution concentration on the dispersion.
3.3.1 Ratio between orifice radius and column radius,
 ${r_n}^*$
${r_n}^*$
The flow of nonuniformity near the orifice is determined by the ratio of the orifice radius and column radius
![]() ${r_n}^*$
. Owing to the convergence, the flow rate in the orifice centre is much greater than that near the sidewall, as discussed in Section 3.1. The variation in local velocity, both in magnitude and direction, causes the solute mass to spread. When the solute front exits, the sidewall lag reduces the average effluent concentration and increases the time over which breakthrough occurs. The dispersive flux of the effluent for several values of
${r_n}^*$
. Owing to the convergence, the flow rate in the orifice centre is much greater than that near the sidewall, as discussed in Section 3.1. The variation in local velocity, both in magnitude and direction, causes the solute mass to spread. When the solute front exits, the sidewall lag reduces the average effluent concentration and increases the time over which breakthrough occurs. The dispersive flux of the effluent for several values of
![]() ${r_n}^*$
is shown in Figure 6, where
${r_n}^*$
is shown in Figure 6, where
![]() $H^* = 2$
for all cases. When
$H^* = 2$
for all cases. When
![]() ${r_n}^*$
is small, that is, with large flow nonuniformity, the breakthrough occurs earlier and the dispersive flux increases earlier, but the peak value is small. It also takes longer for the dispersive flux to return to zero. This means that the average breakthrough of the effluent takes longer for smaller
${r_n}^*$
is small, that is, with large flow nonuniformity, the breakthrough occurs earlier and the dispersive flux increases earlier, but the peak value is small. It also takes longer for the dispersive flux to return to zero. This means that the average breakthrough of the effluent takes longer for smaller
![]() ${r_n}^*$
. The total dispersive flux is also compared (Figure 7). When
${r_n}^*$
. The total dispersive flux is also compared (Figure 7). When
![]() ${r_n}^*$
is small, the dispersive flux is smallest, whereas when the flow is uniform the dispersive flux is the largest.
${r_n}^*$
is small, the dispersive flux is smallest, whereas when the flow is uniform the dispersive flux is the largest.

Figure 6 Dispersive flux time series at the orifice for various orifice radii: top figure
![]() ${r_n}^*$
ranging from 0.6 to 1.0 and bottom figure
${r_n}^*$
ranging from 0.6 to 1.0 and bottom figure
![]() ${r_n}^*$
ranging from 0.1 to 0.5.
${r_n}^*$
ranging from 0.1 to 0.5.

Figure 7 The relationship between the total dispersive flux and the orifice radii.
3.3.2 Ratio between orifice radius and column height,
 ${r_n}^*/H*$
${r_n}^*/H*$
As discussed in Section 3.1, the influence of the converging flow can spread upwards to
![]() $3/2$
of the column radius from the orifice: that is, once
$3/2$
of the column radius from the orifice: that is, once
![]() $H^*> 3/2$
, the column height has no influence on the converging flow pattern. However, equation (3.2) has shown that the BTC depends on the solute travelling time for uniform flow. Therefore, at the orifice, the solute concentration will depend on the column height and, consequently, the total dispersive flux is affected. Figure 8(a) shows the dispersive flux at the orifice in relation to the column height where
$H^*> 3/2$
, the column height has no influence on the converging flow pattern. However, equation (3.2) has shown that the BTC depends on the solute travelling time for uniform flow. Therefore, at the orifice, the solute concentration will depend on the column height and, consequently, the total dispersive flux is affected. Figure 8(a) shows the dispersive flux at the orifice in relation to the column height where
![]() ${r_n}^*$
= 0.14, which is the same as the experimental setting in [Reference Watson, Barry, Schotting and Hassanizadeh30]. It is found that the taller the column, the longer the breakthrough process and the smaller the maximum dispersive flux. However, the total dispersive flux is very close, as shown in Figure 8(b): that is, the column height has little impact on the total dispersive flux when the orifice radius is fixed.
${r_n}^*$
= 0.14, which is the same as the experimental setting in [Reference Watson, Barry, Schotting and Hassanizadeh30]. It is found that the taller the column, the longer the breakthrough process and the smaller the maximum dispersive flux. However, the total dispersive flux is very close, as shown in Figure 8(b): that is, the column height has little impact on the total dispersive flux when the orifice radius is fixed.

Figure 8 (a) Dispersive flux time series at the orifice for various column heights. (b) The relationship between the dispersive flux and the column height.

Figure 9 Dispersive flux time series at the orifice for various dispersivities.
3.3.3 Longitudinal dispersivity,
 ${\alpha _L}^*$
${\alpha _L}^*$
The dispersivity is a material property that determines the spreading of solute in a fluid parcel. Hydrodynamic dispersion for the flow in a column, as shown in Figure 1, will be dominated by the longitudinal dispersivity,
![]() $\alpha _L$
, in the uniform flow zone according to equation (2.2). Using the parameters in Table 2, simulations for various
$\alpha _L$
, in the uniform flow zone according to equation (2.2). Using the parameters in Table 2, simulations for various
![]() $\alpha _L$
were carried out to examine its effect on the dispersion. Figure 9 shows that when
$\alpha _L$
were carried out to examine its effect on the dispersion. Figure 9 shows that when
![]() ${\alpha _L}^*$
increases (0.01275–0.02775), the dispersive flux decreases. However, when
${\alpha _L}^*$
increases (0.01275–0.02775), the dispersive flux decreases. However, when
![]() ${\alpha _L}^*$
keeps increasing from 0.03225 to 0.05525, the dispersive flux increases and flattens out at the end.
${\alpha _L}^*$
keeps increasing from 0.03225 to 0.05525, the dispersive flux increases and flattens out at the end.

Figure 10 (a) Dispersive flux time series and (b) Vertical flow velocity time series at the orifice for various influent concentrations.
3.3.4 Solute concentration of the influent,
 $\omega _{in}$
$\omega _{in}$
Variations in solute concentration, such as for brine, introduce density and viscosity changes in the fluid. Consequently, this will produce convective currents and affect the flow pattern in the column. The impact of the influent solute concentration,
![]() $\omega _{in}$
, is examined using the parameters in Table 1 with
$\omega _{in}$
, is examined using the parameters in Table 1 with
![]() $H* = 2$
and
$H* = 2$
and
![]() ${r_n}^* = 0.14$
:
${r_n}^* = 0.14$
:
![]() $\omega _{in}$
varies from 0.5% to 20%.
$\omega _{in}$
varies from 0.5% to 20%.
The nondimensional dispersive flux is illustrated in Figure 10(a). It can be seen that the breakthrough occurs earliest and lasts longest for the smallest
![]() $\omega_{in}$
. Conversely, for the largest
$\omega_{in}$
. Conversely, for the largest
![]() $\omega _{in}$
, the breakthrough curve will be the steepest. The nondimensional dispersive fluxes for various
$\omega _{in}$
, the breakthrough curve will be the steepest. The nondimensional dispersive fluxes for various
![]() $\omega _{in}$
are listed as in Table 3, where the influent concentration has little impact on the dispersive flux.
$\omega _{in}$
are listed as in Table 3, where the influent concentration has little impact on the dispersive flux.
Table 3 Normalized cumulative dispersive flux for various
![]() $\omega _{in}$
.
$\omega _{in}$
.

When
![]() $\omega _{in}$
is high, the density variation in the miscible zone is large. The denser fluid tends to flow against the inflow direction. This is illustrated in Figure 10(b), which shows the longitudinal velocity at the centre of the orifice. From equations (2.5) and (2.6), the density and viscosity depend on the solute concentration. The ratio
$\omega _{in}$
is high, the density variation in the miscible zone is large. The denser fluid tends to flow against the inflow direction. This is illustrated in Figure 10(b), which shows the longitudinal velocity at the centre of the orifice. From equations (2.5) and (2.6), the density and viscosity depend on the solute concentration. The ratio
![]() $\rho /\mu $
can be calculated using equations (2.5) and (2.6), which apparently decreases with the increase in
$\rho /\mu $
can be calculated using equations (2.5) and (2.6), which apparently decreases with the increase in
![]() $\omega $
. Consequently, the hydraulic conductivity decreases with the increase in
$\omega $
. Consequently, the hydraulic conductivity decreases with the increase in
![]() $\omega $
. Hence, the nondimensional velocity for a higher concentration of brine is greater if all other conditions remain the same, as shown in Figure 10(b).
$\omega $
. Hence, the nondimensional velocity for a higher concentration of brine is greater if all other conditions remain the same, as shown in Figure 10(b).
4 Conclusions
In this study, a multiphysics finite-element model was employed to investigate apparatus-induced dispersion in nonuniform, density-dependent flow within a cylindrical column. The accuracy of the model was validated through comparisons with an analytical solution and laboratory column test data. Our findings can be summarized as follows.
-
(i) The simulations conducted using the model confirmed that flow nonuniformities induced by the apparatus are effectively dissipated within the column when the distance to the outlet exceeds
 $3R/2$
, where R represents the radius of the column. Additionally, we observed that convergent flow in the column apparatus introduced additional hydrodynamic dispersion, primarily when the height of the soil column was relatively small. However, the influence of convergent flow on dispersion diminished when the height of the column exceeded
$3R/2$
, where R represents the radius of the column. Additionally, we observed that convergent flow in the column apparatus introduced additional hydrodynamic dispersion, primarily when the height of the soil column was relatively small. However, the influence of convergent flow on dispersion diminished when the height of the column exceeded
 $3R/2$
.
$3R/2$
. -
(ii) The apparatus-induced dispersion characteristics were found to be influenced by soil properties, such as dispersivity. Moreover, we discovered that an increase in the density gradient of the solution resulted in a decrement in flow velocity at the breakthrough point. This phenomenon played a stabilizing role in the flow dynamics and ultimately led to a reduction in dispersive mixing.
-
(iii) As the dispersion coefficient is known, the dispersive flux increase (or decrease) due to the apparatus, as well as density, can be quantified.
In conclusion, this study provides valuable insights into the phenomenon of apparatus-induced dispersion in nonuniform, density-dependent flow within a cylindrical column. By understanding the dissipation of flow nonuniformities, the effects of convergent flow and the impact of solution density gradient, we can improve our understanding of dispersive mixing phenomena and contribute to the development of more effective strategies for managing and mitigating dispersion in practical applications.
Acknowledgements
This paper is part of a special issue dedicated to honouring the remarkable contributions of Professor Graeme Hocking to the ANZIAM Society, with a specific focus on applied and industrial mathematics.
All the authors of this article have had the distinct privilege of collaborating with Graeme for over 20 years. Hong Zhang embarked on her PhD journey under Graeme’s guidance, studying fluid flow in porous media nearly 30 years ago. Throughout her doctoral studies, Graeme’s invaluable insights and profound knowledge in applied mathematics and fluid dynamics guided and shaped Hong’s research. Following the completion of her PhD, Hong has been incredibly fortunate to continue her association with Graeme, benefiting from his mentorship and enjoying a fruitful professional relationship.