Hostname: page-component-76fb5796d-5g6vh Total loading time: 0 Render date: 2024-04-29T12:56:34.516Z Has data issue: false hasContentIssue false
  • English
  • Français

Spectral refinement using a new projection method

Published online by Cambridge University Press:  17 February 2009

Rekha P. Kulkarni  and
N. Gnaneshwar
Rekha P. Kulkarni
Affiliation:
Department of Mathematics, Indian Institute of Technology, Bombay, Powai, Mumbai 400 076, India; e-mail: rpk@math.iitb.ac.in and gnanesh@math.iitb.ac.in.
N. Gnaneshwar
Affiliation:
Department of Mathematics, Indian Institute of Technology, Bombay, Powai, Mumbai 400 076, India; e-mail: rpk@math.iitb.ac.in and gnanesh@math.iitb.ac.in.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we consider two spectral refinement schemes, elementary and double iteration, for the approximation of eigenelements of a compact operator using a new approximating operator. We show that the new method performs better than the Galerkin, projection and Sloan methods. We obtain precise orders of convergence for the approximation of eigenelements of an integral operator with a smooth kernel using either the orthogonal projection onto a spline space or the interpolatory projection at Gauss points onto a discontinuous piecewise polynomial space. We show that in the double iteration scheme the error for the eigenvalue iterates using the new method is of the order of 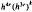, where h is the mesh of the partition and k = 0, 1, 2,… denotes the step of the iteration. This order of convergence is to be compared with the orders 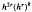in the Galerkin and projection methods and 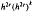in the Sloan method. The error in eigenvector iterates is shown to be of the order of 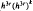in the new method, 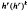in the Galerkin and projection methods and 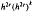in the Sloan method. Similar improvement is observed in the case of the elementary iteration. We show that these orders of convergence are preserved in the corresponding discrete methods obtained by replacing the integration by a numerical quadrature formula. We illustrate this improvement in the order of convergence by numerical examples.

Type
Research Article
Information
The ANZIAM Journal , Volume 46 , Issue 2 , October 2004 , pp. 203 - 224
Copyright
Copyright © Australian Mathematical Society 2004

References

[1]Ahues, M., Largillier, A. and Limaye, B. V., Spectral computations for bounded operators (Chapman and Hall/CRC, New York, 2001).CrossRefGoogle Scholar
[2]Atkinson, K. and Bogomolny, A., “The discrete Galerkin method for integral equations”, Math. Comp. 48 (1987).CrossRefGoogle Scholar
[3]Chatelin, F., Spectral approximation of linear operators (Academic Press, New York, 1983).Google Scholar
[4]de Boor, C., “A bound on the L∞ norm of L2-approximation by splines in terms of a global mesh ratio”, Math. Comp. 30 (1976) 765–771.Google Scholar
[5]de Boor, C. and Swartz, B., “Collocation at Gaussian points”, SIAM J. Numer Anal. 10 (1973) 582–606.CrossRefGoogle Scholar
[6]Deshpande, L. N. and Limaye, B. V., “A fixed point technique to refine a simple approximate eigenvalue and corresponding eigenvector”, Numer. Funct. Anal. Optim. 10 (1989) 909–921.CrossRefGoogle Scholar
[7]Douglas, J. Jr., Dupont, T. and Wahlbin, L., “Optimal L∞ error estimates for Galerkin approximations to solutions of two point boundary value problems”, Math. Comp. 29 (1975) 475–483.Google Scholar
[8]Kulkarni, R. P., “A superconvergence result for solutions of compact operator equations”, Bull. Austral. Math. Soc. 68 (2003) 517–528.CrossRefGoogle Scholar
[9]Kulkarni, R. P., “A new superconvergent projection method for approximate solutions of eigenvalue problems”, Numer Funct. Anal. Optim. 24 (2003) 75–84.CrossRefGoogle Scholar
[10]Kulkarni, R. P. and Limaye, B. V., “Solution of a Schrodinger equation by iterative refinement”, J. Austral. Math. Soc. Ser. B 32 (1990) 115–132.CrossRefGoogle Scholar
[11]Osborn, J. E., “Spectral approximation for compact operators”, Math. Comp. 29 (1975) 712–725.CrossRefGoogle Scholar
[12]Richter, G. R., “Superconvergence of piecewise polynomial Galerkin approximations for Fredholm integral equations of the second kind”, Numer Math. 31 (1978) 63–70.CrossRefGoogle Scholar