I. INTRODUCTION
In the recent years the availability of inexpensive, portable, and highly usable digital multimedia devices (such as cameras, mobile-phones, digital recorders, etc.) has increased the possibility of generating digital audiovisual data without any time, location, and network-related constraints. In addition, the versatility of the digital support allows copying, editing, and distributing the multimedia data with little effort. As a consequence, the authentication and validation of a given content have become more and more difficult, due to the possible diverse origins and the potential alterations that could have been operated. This difficulty has severe implications when the digital content is used to support legal evidences. Digital videos and photographs can be no longer considered “proof of evidence/occurrence” since their origin and integrity cannot be trusted [Reference Farid1]. Moreover, the detection of copyright infringements and the validation of the legal property of multimedia data may be difficult since there is no way to identify the original owner.
From these premises, a significant research effort has been recently devoted to the forensic analysis of multimedia data. A large part of the research activities in this field are devoted to the analysis of still images, since digital photographs are largely used to provide objective evidence in legal, medical, and surveillance applications [Reference Venkatraman and Makur2]. In particular, several approaches target the possibility of validating, detecting alterations, and recovering the chain of processing steps operated on digital images. As a result, nowadays digital image forensic techniques enable to determine: whether an image is original or artificially created via cut and paste operations from different photos; which source generated an image (camera model, vendors); whether the whole image or parts of it have been artificially modified and how; what was the processing history of an image. These solutions rely on the consideration that many processing steps are not reversible and leave some traces in the resulting signal (hereby called “footprints”). Detecting and analyzing these footprints allow the reconstruction of the chain of processing steps. In other words, the detection of these footprints allows a sort of reverse engineering of digital content, in order to identify the type and order of the processing steps that a digital content has undergone, from its first generation to its actual form.
Despite the significant available literature on digital image forensics, video forensics still presents many unexplored research issues, because of the peculiarities of video signals with respect to images and the wider range of possible alterations that can be applied on this type of digital content. In fact, all the potential modifications concerning digital images can be operated both on the single frames of a video sequence and along the temporal dimension. This might be aimed at hiding or erasing details from the recorded scene, concealing the originating source, redistributing the original signal without the owner's permission or pretending on its characteristics (e.g. low-quality contents re-encoded at high quality) [Reference Wang, Farid, Solanki, Sullivan and Madhow3,Reference Wang, Farid, Voloshynovskiy, Dittmann and Fridrich4]. Moreover, forensic analysis of video content proves to be harder with respect to the analysis of still images since video data are practically always available in compressed formats and several times a high compression factor is used to store it. Strong compression ratios may cancel or fatally compromise the existing footprints so that the processing history is, entirely or in part, no longer recoverable.
On top of that, forensic analysts must now face the problem of anti-forensic techniques, which consist in modifying the forging process in order to make the unauthorized alterations transparent to forgery detection algorithms. Since each of these techniques is usually targeted to erase one specific trace left during the manipulation, anti-forensic methods are very heterogeneous. Nevertheless, all of them should satisfy two basic principles: do not hinder significantly the quality of the forged content that is produced; do not introduce artifacts that are easily detectable, so that anti-forensic techniques could be countered by the content owner. Although most of the anti-forensic strategies presented in literature have been developed for still images only, there are some techniques concerning video data.
The original contribution of this paper relies in providing an overview of the main forensic techniques that have been designed so far in the video content analysis. Previous overview papers in the literature mainly address image forensics and just a few details are provided about video content analysis. We believe that video forensic analysis has been maturely developed so that a review of the proposed techniques is widely justified.
In the following, we outline the structure of the paper. Section II provides the necessary background on digital image forensics, as it provides the foundations for analogous techniques targeting video content. The remaining sections deal with various aspects related to video forensics. We start addressing video acquisition in Section III, presenting several strategies to identify the device that captured a given video content. Then, in Section IV we consider the traces left by video coding, which are used to determine, e.g., the coding parameters, the coding standard, or the number of multiple compression steps. Video doctoring is addressed in Section V, which presents forensic analysis methods based on detecting inconsistencies in acquisition and coding-based footprints, as well as methods that reveal traces left by the forgery itself. Section VI concludes the survey, indicating open issues in the field of video forensics that might be tackled by future research efforts.
II. A QUICK OVERVIEW OF THE STATE-OF-THE-ART IN IMAGE FORENSICS
As mentioned in the previous section, image forensic tools have been widely studied in the past years due to the many applications of digital images that require some kind of validation. Many of them can be applied to video signals as well by considering each frame as single images, while others can be extended including the temporal dimension as well.
For this reason, a preliminary review of the state-of-the-art on image forensics is necessary in order to outline the baseline scenario from where video forensics departs. Many detailed overviews can be found in literature on digital image forensics (e.g. see [Reference Sencar and Memon5,Reference Poisel and Tjoa6]). Here, we just outline some of the most important works that offered a sort of common background for the current and future video forensic techniques. In particular, we will discuss methods dealing with camera artifacts, compression footprints, and geometric inconsistencies.
The methods that follow enable to perform image authentication and, in some cases, tampering localization, without resorting to additional side information explicitly computed by the content owner. This is in contrast with other approaches based on, e.g., digital watermarking [Reference Fridrich7,Reference Eggers and Girod8] or multimedia hashing [Reference Venkatesan, Koon, Jakubowski and Moulin9–Reference Lin, Varodayan and Girod13], or a combination of both [Reference Valenzise, Tagliasacchi, Tubaro, Cancelli and Barni14].
A) Camera artifacts
Studies on camera artifacts that are left during the acquisition pipeline have laid the basis for image forensics. The far more studied artifact is the multiplicative noise introduced by CCD/CMOS sensors, named photo response non-uniformity (PRNU) noise. PRNU has been exploited both for digital camera identification [Reference Lukas, Fridrich and Goljan15] and for image integrity verification [Reference Chen, Fridrich, Goljan and Lukás16], and it proves to be a reliable trace also when an image is compressed using the JPEG codec.
Since common digital cameras are equipped with just one sensor, color images are obtained by overlaying a color filter array (CFA) to it, and using a demosaicing algorithm for interpolating missing values. The specific correlation pattern introduced during this phase allows to perform device model identification and tampering detection [Reference Popescu and Farid17], provided that images are not (or very little) compressed.
The last artifact that we mention is chromatic aberration, that is due to the camera lens shape; inconsistencies in this effect can be searched on to identify tampered regions in the image, as explained in [Reference Johnson, Farid, Voloshynovskiy, Dittmann and Fridrich18,Reference Yerushalmy and Hel-Or19].
B) Image compression
A significant investigation activity has been carried on image coding forensics since the lossy nature of many compression strategies leaves peculiar traces on the resulting images. These footprints allow the forensic analyst to infer whether an image has been compressed, which encoder and which parameters have been used, and if the image has undergone multiple compression steps [Reference Milani, Tagliasacchi and Tubaro20]. In order to understand whether an image has been compressed, in [Reference Fu, Shi and Su21] the authors show how to exploit a statistic model called Benford's law. Alternatively, in [Reference Liu and Heynderickx22], the authors focus on identifying if an image has been block-wise processed, also estimating the horizontal and vertical block dimensions. If the image has been compressed, in [Reference Lin, Tjoa, Zhao and Liu23] the authors propose a method capable of identifying the used encoder, which is useful, for example, to differentiate between discrete cosine transform (DCT)- and DWT-based coding architectures. A method to infer the quantization step used for a JPEG compressed image is shown in [Reference Fan and de Queiroz24,Reference Fan and de Queiroz25]. Finally, in [Reference Lukás and Fridrich26–Reference Bianchi and Piva30] the authors propose some methods to expose double JPEG compression based on the analysis of the histograms of DCT coefficients.
C) Geometric/physics inconsistencies
Since human brain is notoriously not good in calculating projections and perspectives, most forged images contain inconsistencies at the “scene” level (e.g. in lighting, shadows, perspective, etc.). Although being very difficult to perform in a fully automatic fashion, this kind of analysis is a powerful instrument for image integrity verification. One of the main advantages of this approach is that, being fairly independent on low-level characteristics of images, it is well suited also for strongly compressed or low-quality images.
Johnson and Farid proposed a technique allowing to detect inconsistencies in scene illumination [Reference Johnson and Farid31] and another one that reveals inconsistencies in spotlight reflection in human eyes [Reference Johnson, Farid, Furon, Cayre, Doërr and Bas32]. Zhang et al. [Reference Zhang, Cao, Zhang, Zhu and Wang33] introduced methods for revealing anomalous behavior of shadows geometry and color. Also, inconsistencies in the perspective of an image have been exploited, for example, in the work from Conotter et al. [Reference Conotter, Boato and Farid34], which detects anomalies in the perspective of signs and billboards writings.
III. FORENSIC TOOLS FOR VIDEO ACQUISITION ANALYSIS
The analysis of image acquisition is one of the earliest problems that emerged in multimedia forensics, being very similar to the “classical” forensic technique of ballistic fingerprinting. Its basic goal is to understand the very first steps of the history of a content, namely identifying the originating device. The source identification problem has been approached from several standpoints. We may be interested in understanding: (i) which kind of device/technique generated the content (e.g. camera, scanner, photo realistic computer graphics, etc.), (ii) which model of a device was used or, more specifically, (iii) which device generated the content.
Different techniques address each of these problems in image forensics, and some of them have naturally laid the basis for the corresponding video forensic approaches. However, Section III (A) will show that source identification has not yet reached a mature state in the case of videos.
Another interesting application that recently emerged in the field of video forensics is the detection of illegal reproductions, noticeably bootlegs videos and captured screeenshots. This problem will be separately discussed in Section III (B).
Before deepening the discussion, we introduce in Figure 1 a simplified model of the acquisition chain, when a standard camcorder is adopted. First, the sensed scene is distorted by optical lenses and then mosaiced by an RGB CFA. Pixel values are stored on the internal CCD/CMOS array, and then further processed by the in-camera software. The last step usually consists in lossy encoding the resulting frames, typically using MPEG-x or H.26x codecs for cameras and 3GP codecs for mobile phones (see Section IV). The captured images are then either displayed/projected on screen or printed, and can be potentially recaptured with another camera.
A) Identification of acquisition device
In the field of image forensics, many approaches have been developed to investigate each of the aforementioned questions about the acquisition process. Conversely, the works on video forensics assume that the content has been recorded using a camcorder, or a modern cell phone. To the best of our knowledge, no video-specific approaches have been developed to distinguish between computer graphics and real scenes. Instead, all the works in this field focus on identifying the specific device that originated a given content.
Kurosawa et al. [Reference Kurosawa, Kuroki and Saitoh35] were the first to introduce the problem of camcorder fingerprinting. They proposed a method to identify individual video cameras or video camera models by analyzing videotaped images. They observed that dark-current noise of CCD chips, that is determined during the manufacturing process, creates a fixed pattern noise, which is practically unique for each device, and they also proposed a way to estimate this fixed pattern. Due to very strong hypotheses on the pattern extraction procedure (hundreds of frames recording a black screen were needed) this work did not allow to understand if a given video came from a specific camera. Nevertheless, it can be considered as one of the pioneering works in video forensics. Later, research in image forensics demonstrated that PRNU noise could provide a much more strong and reliable fingerprint of a CCD array and, consequently, more recent works targeting source identification for video are based on this kind of feature.
PRNU BASED SOURCE IDENTIFICATION
Many source identification techniques in image forensics exploit the PRNU noise introduced by the sensor. Although not being the only kind of sensor noise [Reference Holst36], PRNU has proven to be the most robust feature. Indeed, being a multiplicative noise, it is difficult for device manufacturers to remove it. First, we describe how this method works in the case of images. Then, we discuss its extension to videos, highlighting the challenging issues that arise.
Given a noise free image I 0, the image I acquired by the sensor is modeled as
where γ is a multiplicative factor, K is the PRNU noise, and N models all the other additive noise sources (see [Reference Holst36] for details). Note that all operations are intended element-wise.
If we could perfectly separate I from I 0, it would be easy to compute a good estimate of K from a single image. Unfortunately, this cannot be done in general: separating content from noise is a challenging task, as demonstrated by several works on image denoising. Consequently, the common approach is to estimate K from a group of authentic images I j, j = 1, …, n. Each image I j is first denoised using an appropriate filter. Then, the denoised version ![]() is subtracted from I j, yielding
is subtracted from I j, yielding
where W j is the residual noise for the jth image. The PRNU is then estimated as
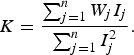
From a technical point of view, two factors are of primary importance to obtain a good estimate of K:
1. using a group of flat, well illuminated images, e.g. pictures of a wall, of the sky, etc. Few tens of images usually suffice;
2. choosing an appropriate denoising filter (see [Reference Amerini, Caldelli, Cappellini, Picchioni and Piva37]).
Once K is obtained for a device, checking if a query image S has been generated from that device reduces to evaluating the correlation between the noise component of the query image and the reference noise of the device. Formally, S is denoised with the same filter and subtracted from itself, yielding W S. Then, the correlation between the query image and the PRNU mask is obtained as
where the operator ⊗ denotes normalized correlation. The value of ρ is usually low (e.g. ρ ≃ 0.2) even for images that were actually acquired with the device that originated the mask. However, ρ is sufficiently discriminative, since correlation values with extraneous images is smaller by two or three orders of magnitude. Furthermore, experiments demonstrated that this kind of analysis is robust to JPEG compression at large quality factors (e.g. >80%).
Having provided the background for PRNU-based source identification in the case of still images, we move the scope of the discussion to the case of videos. At a first glance, it may seem that estimating the PRNU of a camcorder from a video sequence should be easier, due to the usually large amount of frames available. However, this is not true for two main reasons. First, typical spatial resolution of videos is much lower than that of images. Second, frames usually undergo strong quantization and aggressive coding that introduce more artifacts than those affecting JPEG-compressed images.
The first work about camcorder identification was proposed by Chen et al. [Reference Chen, Fridrich, Goljan and Lukás38]. They rely on the method described above for extracting the PRNU mask. However, a significant effort is devoted to the proper choice the denoising filter, which led to the selection of a wavelet-based filter designed to remove Gaussian noise [Reference Kivanc Mihcak, Kozintsev and Ramchandran39]. In addition, a pre-processing step is included to mitigate quantization artifacts introduced by lossy coding. More specifically, the authors observe that blocking artifacts and ringing artifacts at frame boundaries (introduced to adjust the size of the frame to a multiple of the block size) introduce a noise pattern that strongly depends on the compression algorithm rather than on the acquisition hardware. They propose a method to identify the frequencies of the DFT transform where such noise contribution is located and suppress them, thus increasing noticeably the performance of the estimation. The experiments in [Reference Chen, Fridrich, Goljan and Lukás38] showed that a tradeoff exists between video quality (in terms of bitrate) and length to achieve successful detection. If the video is compressed at high quality (e.g. 4–6 Mb/s), then a relatively short sequence (40 s) suffices for a good estimation of the mask. Conversely, for low quality videos (e.g. 150 Kb/s) the length of the training sequence must be doubled to obtain comparable performance.
The challenging problem of video source identification from low-quality videos has been deeply explored by van Houten et al. [Reference van Houten, Geradts, Franke, Veenman, Ünay, Çataltepe and Aksoy40–Reference van Houten and Geradts42] in several works. The authors recorded videos using several different cameras, with various resolutions and bitrates. Then, they uploaded these videos on YouTube and downloaded them. Since YouTube re-encodes video during uploading, frames underwent at least double compression. After a large set of experiments, the authors came to the final conclusion that PRNU-based source identification is still possible for very low-quality videos, provided that the forensic analyst can extract the PRNU mask from a flat field video and that the aspect ratio of the video is not (automatically) changed during uploading.
In all the aforementioned works, video compression is considered to be a factor significantly hindering the identification of the PRNU-related footprints. However, digital video content mainly exists in compressed format, and the first compression step is operated by the camera itself using a proprietary codec. Therefore, the identification of the acquisition device could also be based on the identification the codec, leveraging the techniques described in Section IV.
B) Detection of (illegal) reproduction of videos
An important problem in copyright protection is the proliferation of bootleg videos: many illegal copies of movies are made available on the Internet even before their official release. A great deal of these fake copies are produced by recording films with camcorders in cinemas (the last steps reported in Fig. 1). Video forensics contributes to facing these problems by: (i) detecting re-projected videos, as described in Section III. (B)(1); (ii) providing video retrieval technique based on device fingerprinting described in Section III B(2).

Fig. 1. Typical acquisition pipeline: light enters the camera through the lens, is filtered by the CFA and converted to a digital signal by the sensor. Usually, this is followed by some in-camera post-processing and compression. In some cases, the video can be projected/displayed and re-acquired with another camera, usually undergoing lighting and spatial distortions.
DETECTION OF RE-ACQUISITION
Re-acquisition occurs when a video sequence that is reproduced on a display or projected on a screen is recaptured. In the literature, some approaches were proposed based on active watermarking to perform both the identification of bootleg video [Reference Lee, Kim, Lee, Oh, Suh and Lee43] and to locate pirate's position in cinemas [Reference Lee, Kim and Lee44]. Recently, blind techniques are also emerging. Wang and Farid [Reference Wang, Farid, Solanki, Sullivan and Madhow3] developed the most significant work in this field, exploiting the principles of multiple view geometry. They observed that re-acquisition captures a scene that is constrained to belong to a planar surface (e.g. the screen), whereas the original acquisition of the video was taken projecting objects from the real world to the camera plane. The authors show both mathematically and experimentally that re-projection usually causes non-zero skewFootnote 1 in the intrinsic matrix of the global projection. Assuming that the skew of the camera used for the first acquisition was zero, significant deviations of this parameter in the estimated intrinsic matrix can be used as evidence that a video has been re-projected. Although very promising, this approach suffers from some limitations. Specifically, the original acquisition is modeled under several simplifying hypotheses, and skew estimation on real-world video is difficult to perform without supervision. In [Reference Wang, Farid, Solanki, Sullivan and Madhow3], many experiments are conducted in a synthetic setting, yielding good performance (re-projected videos are detected with 88% accuracy and with 0.4% false alarm probability). However, only one experiment is based on real-world video content, presumably because of the complexity of skew estimation in this setting.
Lee et al. [Reference Lee, Lee, Oh, Ryu and Lee45] addressed the problem of detecting if an image might be a screenshot re-captured from an interlaced video. In an interlaced video, half of the lines are recorded at time t in the field f(x, y, t), and the other half are recorded at time t + 1 in the field f (x, y, t + 1). There are several possible ways to obtain the full (spatial) resolution frame, i.e. F (x, y, t), and one of the simplest is to weave fields together, as in Fig. 2. Therefore, lines of the full resolution frame are acquired at different, though very near, time instants. If the video contains rapidly moving objects (or, equivalently, the camera is moving rapidly), this will introduce artifacts that are referred to as “combing”. In [Reference Lee, Lee, Oh, Ryu and Lee45], the authors exploit the directional property of combing artifacts to devise six discriminative features. These features are extracted from wavelet transform subbands (since combing artifacts are most evident near edges) and from vertical and horizontal differential histograms (which will expose strong differences in the presence of such artifacts). Experimental results show an average accuracy higher than 97%.

Fig. 2. A simple field weaving algorithm for video de-interlacing. This scheme uses T fields to produce a de-interlaced video of T/2 frames.
DETECTION OF COPYING
The most common approach in video copy detection is to extract salient features from visual content that do not depend on the device used to capture the video. However, in [Reference Bayram, Sencar, Memon, Lew, Bimbo and Bakker46], Bayram et al. pointed out that robust content-based signatures may hinder the capability of distinguishing between videos which are similar, although they are not copies of each other. This issue might arise, e.g., in the case of videos taken by two different users of the same scene. For this reason, they proposed to use source device characteristics extracted from videos to construct a copy detection technique. In [Reference Bayram, Sencar, Memon, Lew, Bimbo and Bakker46], a video signature is obtained by estimating the PRNU fingerprints of camcorders involved in the generation of the video. The authors suggest to compute the PRNU fingerprint in the classical way. In the case of professional content, video is usually acquired using more than one device. As a consequence, this automatically yields a weighted mean of the different PRNU patterns, in which more frames taken with the same camera will result in a stronger weight assigned to it. Furthermore, it was observed that PRNU signatures are not totally insensible to the underlying frame content. Therefore, the weighted mean will also implicitly carry information about the content of the video. Notice that this method aims at obtaining a fingerprint for the content rather than for the device. Although it reuses PRNU fingerprinting techniques described in Section III. A(1), it does so with a completely different objective. The authors also show that the fingerprint is robust against a set of common processing operations, i.e., contrast enhancement, blurring, frame dropping, subtitles, brightness adjustment, compression. Experiments performed on video downloaded from YouTube show a 96% detection rate for a 5% false alarm probability. However, slight rotation or resizing, not mentioned in [Reference Bayram, Sencar, Memon, Lew, Bimbo and Bakker46], are likely to completely destroy the fingerprint.
IV. FORENSIC TOOLS FOR VIDEO COMPRESSION
Video content is typically available in a lossy compression format due to the large bit rate that is necessary to represent motion pictures either in an uncompressed or lossless format. Lossy compression leaves characteristic footprints, which might be detected by the forensic analyst. At the same time, the study of effective forensic tools dealing with compressed videos is a challenging task since coding operations have the potential effect of erasing the footprints left by previous manipulations. In this way, the processing history cannot be recovered anymore. Moreover, the wide set of video coding architectures that have been standardized during the last two decades introduces several degrees of freedom in the way different compression steps can be composed. As such, the codec adopted to compress a video sequence represents a distinctive connotative element. Therefore, if detected, it can be useful for the identification of the acquisition device, as well as for revealing possible manipulations.
Most of the existing video coding architectures build on top of coding tools originally designed for images. The JPEG standard is, by far, the most widely adopted coding technique for still images and many of its principles are reused for the compression of video signals [Reference Wallace47]. A JPEG codec converts color images into a suitable color space (e.g. YCbCr), and processes each color component independently. The encoder operates according to three main steps:
• The image is divided into non-overlapping 8 × 8 pixel blocks X = [X(i,j), i,j = 0, …, 7, which are transformed using a DCT into coefficients Y(i, j) (grouped into 8 × 8 blocks Y).
• The DCT coefficients Y(i, j) are uniformly quantized into levels Y q(i, j) with quantization steps Δ(i, j), which depend on the desired distortion and the spatial frequency (i, j), i.e.
(5)
At the decoder, the reconstructed DCT coefficients Y r(i, j) are obtained by multiplying the quantization levels, i.e., Y r(i,j) = Y q(i,j) Δ(i,j).
• The quantization levels Y q(i, j) are lossless coded into a binary bitstream by means of Huffman coding tables.
Video coding architectures are more complex than those adopted for still images. Most of the widely used coding standards (e.g. those of MPEG-x or H.26x families) inherit the use of block-wise transform coding from the JPEG standard. However, the architecture is complicated by several additional coding tools, e.g., spatial and temporal prediction, in-loop filtering, image interpolation, etc. Moreover, different transforms might be adopted within the same coding standard.
Fig. 3 illustrates a simplified block diagram representing the main steps in a conventional video coding architecture. First, the encoder splits the video sequence into frames, and each frame is divided into blocks of pixels X. Each block is subtracted to a prediction generated by P exploiting either spatial and/or temporal correlation. Then, the prediction residual is encoded following a sequence of steps similar to those adopted by the JPEG standard. In this case, though, the values of the quantization steps and the characteristics of transform might change according to the specific standard.

Fig. 3. Simplified block diagram of a conventional video codec. P computes the prediction, T the orthonormal transform, Q is the quantizer, and F is responsible of rounding and in-loop filtering.
Quantization is a non-invertible operation and it is the main source for information loss. Thus, it leaves characteristic footprints, which depend on the chosen quantization steps and quantization strategy. Therefore, the analysis of coding-based footprints might be leveraged to: (i) infer details about the encoder (e.g. coding standard, coding parameters, non-normative tools); (ii) assess the quality of a sequence in a no-reference framework; or (iii) study the characteristics of the channel used to transmit the sequence.
In addition, block-wise processing introduces an artificial partition of the coded frame, which is further enhanced by the following processing steps. Unlike JPEG, the actual partitioning strategy is not fixed, as it depends on the specifications of coding standard and on the adopted rate–distortion optimization policy. Therefore, blockiness artifacts can be used to infer information about the adopted codec.
Finally, different codec implementations may adopt diverse spatial or temporal prediction strategies, according to rate–distortion requirements and computational constraints. The identification of the adopted motion vectors and coding modes provides relevant footprints that can be exploited by the forensic analyst, e.g. to validate the originating devices.
When each frame is considered as a single image, it is possible to apply image-based forensic analysis techniques. However, to enable a more thorough analysis, it is necessary to consider coding operations along the temporal dimension. In the following, we provide a survey of forensic tools aimed at reconstructing the coding history of video content. Whenever applicable, we start by briefly illustrating the techniques adopted for still images. Then, we show how they can be modified, extended, and generalized to the case of video.
A) Video coding parameter identification
In image and video coding architectures, the choice of the coding parameters is driven by non-normative tools, which depend on the specific implementation of the codec and on the characteristics of the coded signal. In JPEG compression, the user-defined coding parameters are limited to the selection of the quantization matrices, which are adopted to improve the coding efficiency based on the psycho-visual analysis of human perception. Conversely, in the case of video compression, the number of coding parameters that can be adjusted is significantly wider. As a consequence, the forensic analyst needs to take into account a larger number of degrees of freedom when detecting the codec identity. This piece of information might enable the identification of vendor-dependent implementations of video codecs. As such, it could be potentially used to: (i) verify intellectual property infringements; (ii) identify the codec that generated the video content; (iii) estimate the quality of the reconstructed video without the availability of the original source. In the literature, the methods aiming at estimating different coding parameters and syntax elements characterizing the adopted codec can be grouped into three main categories, which are further described below: (i) approaches detecting block boundaries; (ii) approaches estimating the quantization parameters, and (iii) approaches estimating the motion vectors.
BLOCK DETECTION
Most video coding architectures encode frames on a block-by-block basis. For this reason, artifacts at block boundaries can be exploited to reveal traces of previous compression steps. Typical blocking artifacts are shown in Fig. 4. Identifying block boundaries allows also estimating the block size. It is possible to detect block-wise coding operations by checking local pixel consistency, as shown in [Reference Fan and de Queiroz24,Reference Fan and de Queiroz25]. There, the authors evaluate whether the statistics of pixel differences across blocks differ from those of pixels within the same block. In this case, the image is supposed to be the result of block-wise compression.

Fig. 4. Original (a) and compressed (b) frames of a standard video sequence. The high compression rate is responsible for blocking artifacts.
In [Reference Li and Forchhammer48], the block size in a compressed video sequence is estimated by analyzing the reconstructed picture in the frequency domain and detecting those peaks that are related to discontinuities at block boundaries, rather than intrinsic features of the underlying image.
However, some modern video coding architectures (including, e.g., H.264/AVC as well as the recent HEVC standard under development) enable to use a deblocking filter to smooth artifacts at block boundaries, in addition to variable block sizes (also with non-square blocks). In these situations, traditional block detection methods fail, leaving this as an open issue for further investigations.
QUANTIZATION STEP DETECTION
Scalar quantization in the transform domain leaves a very common footprint in the histogram of transform coefficients. Indeed, the histogram of each coefficient Y r(i, j) shows a typical comb-like distribution, in which the peaks are spaced apart by Δ(i, j), instead of a continuous distribution (Fig. 5). Ideally, the distribution can be expressed as follows:
where δ is the Dirac delta function and w k are weights that depend on the original distribution (note that indexes (i, j) are omitted for the sake of clarity). For this reason, the quantization step Δ(i, j) can be recovered by studying the distance between peaks of these histograms.

Fig. 5. Histograms of DCT coefficients (c 1, c 2, c 3) before (first row) and after (second row) quantization. The quantization step Δ(i, j) can be estimated by the gaps between consecutive peaks.
To this end, the work in [Reference Fan and de Queiroz24,Reference Fan and de Queiroz25] proposes to exploit this footprint to estimate the quality factor of JPEG compression. Specifically, the envelope of the comb-shaped histogram is approximated by means of a Gaussian distribution for DC coefficients, and a Laplacian distribution for AC coefficients. Then, the quality factor is estimated with a maximum likelihood (ML) approach, where the quantized coefficients are used as observations, and data coming from uniform and saturated blocks is discarded to make the estimation more robust.
In [Reference Ye, Sun and Chang49] the authors propose a method for estimating the elements of the whole quantization table. Separate histograms are computed for each DCT coefficient subband (i, j). Analyzing the periodicity of the power spectrum, it is possible to extract the quantization step Δ(i, j) for each subband. Periodicity is detected with a method based on the second-order derivative applied to the histograms.
In [Reference Lin, Tjoa, Zhao and Liu23], another method based on the histograms of DCT coefficients is proposed. There, the authors estimate the quantization table as a linear combination of existing quantization tables. A first estimate of the quantization step size for each DCT band is obtained from the distance between adjacent peaks of the histogram of transformed coefficients. However, in most cases, high-frequency coefficients do not contain enough information. For this reason some elements of the quantization matrix cannot be reconstructed, and they are estimated as a linear combination (preserving the already obtained quantization steps) of other existing quantization tables collected into a database.
A similar argument can be used to estimate the quantization parameter in video coding, when the same quantization matrix is used for all blocks in a frame. In [Reference Chen, Challapali and Balakrishnan50,Reference Tagliasacchi and Tubaro51], the authors consider the case of MPEG-2 and H.264/AVC coded video, respectively. There, the histograms are computed from DCT coefficients of prediction residuals. To this end, motion estimation is performed at the decoder side to recover an approximation of the motion-compensated prediction residuals available at the encoder.
Based on the proposed method for quantization step estimation a possible future line of investigation could be the inference of the rate-control algorithm applied at the encoder side, by tracking how quantization parameters vary over time. This could be an important hint to identify vendor-specific codec implementations.
IDENTIFICATION OF MOTION VECTORS
A significant difference between image and video coding is the use of predictors exploiting temporal correlation between consecutive frames. The idea is that of reducing temporal redundancy by exploiting similarities among neighboring video frames. This is achieved constructing a predictor of the current video frame by means of motion estimation and compensation. In most video coding architectures, a block-based motion model is adopted. Therefore, for each block, a motion vector (MV) is estimated, in such a way to generate a motion-compensated predictor. In [Reference Valenzise, Tagliasacchi and Tubaro52], it is shown how to estimate, at the decoder, the motion vectors originally adopted by the encoder, also when the bitstream is missing. The key tenet is to perform motion estimation by maximizing, for each block, an objective function that measures the comb-like shape of the resulting prediction residuals in the DCT domain.
Although the estimation of coding parameters has been investigated, mainly focusing on block detection and quantization parameter estimation, there are still many unexplored areas due to the wide variety of coding options that can be enabled and the presence of a significant number of non-normative aspects in the standard definition (i.e. rate–distortion optimization, motion estimation algorithm, etc.). These coding tools offer a significant amount of degrees of freedom to the video codec designer, who can implement in different ways an encoder producing a bitstream compliant with the target coding standard. On the other hand, the task of forensic analyst becomes more and more difficult, when it comes to characterize and detect the different footprints left by each operation.
B) Video re-encoding
Every time a video sequence that has already been compressed is edited (e.g. scaling, cropping, brightness/contrast enhancement, local manipulation, etc.), it has to be re-compressed. Studying processing chains consisting of multiple compression steps is useful, e.g. for tampering detection or to identify the original encoder being used. This is a typical situation that arises, e.g. when video content is downloaded from video-sharing websites.
Of course, it is straightforward to obtain the parameters used in the last compression stage, as they can be read directly from the bitstream. However, it is much more challenging to extract information about the previous coding steps. For this reason, some authors have studied the footprints left by double video compression. The solutions proposed so far in the literature are mainly focused on MPEG video, and they exploit the same ideas originally used for JPEG double compression.
DOUBLE COMPRESSION
Double JPEG compression can be approximated by double quantization of transform coefficients Y(i, j), such that
where indexes (i, j) have been omitted for the sake of clarity. Re-quantizing already quantized coefficients with different quantization step sizes affects the histogram of DCT coefficients. For this reason, most solutions are based on the statistical footprints extracted from such histograms.
In [Reference Lukás and Fridrich26], Lukáš and Fridrich show how double compression introduces characteristic peaks in the histogram, which alter the original statistics and assume different configurations according to the relationship between the quantization step sizes of consecutive compression operations, i.e., respectively, Δ1 and Δ2. More precisely, the authors highlight how peaks can be more or less evident depending on the relationship between the two step sizes, and propose a strategy to identify double compression. Special attention is paid to the presence of double peaks and missing centroids (i.e. those peaks with very small probability) in the DCT coefficient histograms, as they are identified to be robust features providing information about the primary quantization. Their approach relies on cropping the reconstructed image (in order to disrupt the structure of JPEG blocks) and compressing it with a set of candidate quantization tables. The image is then compressed using Δ2(i,j) and the histogram of DCT coefficients is computed. The proposed method chooses the quantization table such that the resulting histogram is as close as possible to that obtained from the reconstructed image. This method is further explored in [Reference He, Lin, Wang and Tang53], providing a way to automatically detect and locate regions that have gone through a second JPEG compression stage. A similar solution is proposed in [Reference Pevny and Fridrich54], which considers only the histograms related to the nine most significant DCT subbands, which are not quantized to zero. The corresponding quantization steps, i.e. those employed in the first compression stage, are computed via a support vector machine classifier. The remaining quantization steps are computed via a ML estimator.
A widely adopted strategy for the detection of double compression relies on the so-called Benford's law or first digit law [Reference Fu, Shi and Su21]. In a nutshell, it relies on the analysis of the distribution of the most significant decimal digit m (also called “first digit”) of the absolute value of quantized transformed coefficients. Indeed, in the case of an original uncompressed image, the distribution is closely related to the Benford's equation or its generalized version, i.e.,

respectively (where N is a normalizing constant). Whenever the empirical distribution deviates significantly from the interpolated logarithmic curve, it is possible to infer that the image was compressed twice. Then, it is also possible to estimate the compression parameters of the first coding stage. Many double-compression detection approaches based on Benford's law have been designed focusing on still images [Reference Fu, Shi and Su21], giving detection accuracy higher than 90%. These solutions have also been extended to the case of video signals, but the prediction units (spatial or temporal) that are part of the compression scheme reduce the efficiency of the detector, leading to an accuracy higher than 70%. More recently, this approach has also been extended to the case of multiple JPEG compression steps since in many practical cases images and videos are compressed more than twice [Reference Milani, Tagliasacchi and Tubaro20].
In [Reference Wang, Farid, Voloshynovskiy, Dittmann and Fridrich4], the authors address the problem of estimating the traces of double compression of an MPEG coded video. Two scenarios are considered, depending on whether the group of pictures (GOP) structure used in the first compression is preserved or not. In the former situation, every frame is re-encoded in a frame of the same kind, so that I,B, or P frames remain, respectively, I,B, or P. Since encoding I-frames is not dissimilar from JPEG compression, when an I-frame is re-encoded at a different bitrate, DCT coefficients are subject to two levels of quantization. Therefore, the histograms of DCT coefficients assume a characteristic shape that deviates from the original distribution. In particular, when the quantization step size decreases from the first to the second compression, some bins in the histogram are left empty. Conversely, when the step size increases, the histogram is affected in a characteristic way. Instead, the latter situation typically arises in the case of frame removal or insertion attacks. Since the GOP structure is changed, I-frames can be re-encoded into another kind of frame. However, this gives rise to larger prediction residuals after motion compensation. The authors show that by looking at the Fourier transform of the energy of the displaced frame difference over time, the presence of spikes reveals a change in the GOP structure, which is a clue of double compression.
In [Reference Luo, Wu and Huang55], the authors propose another method for detecting MPEG double-compression based on blocking artifacts. A metric for computing the block artifact strength (BAS) for each frame is defined. This score is inspired to the method in [Reference Fan and de Queiroz25] and relies on the difference of pixel values across a grid. The mean BAS is computed for sequences obtained removing from 1 to 11 frames, obtaining a feature vector of BAS values. If the sequence has been previously tampered with by frame removal and re-compression, the feature vector presents a characteristic behavior.
In [Reference Wang and Farid56], MPEG double quantization detection is addressed on a macroblock-by-macroblock basis. In particular, a probability distribution model for DCT coefficients of a macroblock in an I-frame is discussed. With an estimation-maximization (EM) technique, the probability distribution that would arise if a macroblock were double quantized is estimated. Then, such distribution is compared with the actual distribution of the coefficients. From this comparison, the authors extract the probability that a block has been double compressed. These solutions can be extended to enable the detection of double video compression even in a realistic scenario in which different codecs are employed in each compression stage.
The approach in [Reference Bestagini, Allam, Milani, Tagliasacchi and Tubaro57] presents an effective codec identification strategy that allows to determine the codec used in the first compression stage in the case of double video compression (note that the codec used in the second compression stage is known since the bitstream is usually available). The proposed algorithm relies on the assumption that quantization is an idempotent operator, i.e., whenever a quantizer is applied to a value that has already been previously quantized and reconstructed by the same quantizer, the output value is highly correlated with the input value. As a matter of fact, it is possible to identify the adopted codec and its configuration by re-encoding the analyzed sequence a third time, with different codecs and parameter settings. Whenever the output sequence presents the highest correlation with the input video, it is possible to infer that the adopted coding set-up corresponds to that of the first compression.
Although the detection of double compression for images is a widely investigated issue, double video compression still proves to be an open research problem, because of the complexity and diversity of video coding architectures. Whenever two different codecs are involved with similar parameters, the detection of double video compression becomes significantly more difficult [Reference Bestagini, Allam, Milani, Tagliasacchi and Tubaro57]. Moreover, multiple compression is a current and poorly explored topic despite the fact that multimedia content available on the internet has been often coded more than twice [Reference Milani, Tagliasacchi and Tubaro20].
C) Network footprints identification
Video transmission over a noisy channel leaves characteristic footprints in the reconstructed video content. Indeed, packet losses and errors might affect the received bitstream. As a consequence, some of the coded data will be missing or corrupted. Error concealment is designed to take care of this, trying to recover the correct information and mitigate the channel-induced distortion. However, this operation introduces some artifacts in the reconstructed video, which can be detected to infer the underlying loss (or error) pattern. The specific loss pattern permits the identification of the characteristics of the channel that was employed during the transmission of the coded video. More precisely, it is possible to analyze the loss (error) probability, the burstiness, and other statistics related to the distribution of errors in order to identify, e.g. the transmission protocol or the streaming infrastructure.
Most of the approaches targeting the identification of network footprints are intended for no-reference quality monitoring, i.e. the estimation of the quality of the video sequence without having access to the original source as a reference signal. These solutions are designed to provide network devices and client terminals with effective tools that measure the quality-of-experience offered to the end user. The proposed approaches can be divided into two main groups.
The first class of network footprint identification algorithms takes into consideration transmission statistics to estimate the channel distortion on the reconstructed sequence. In [Reference Reibman and Poole58], the authors present an algorithm based on several quality assessment metrics to estimate the packet loss impairment in the reconstructed video. However, the proposed solution adopts full-reference quality metrics that require the availability of the original uncompressed video stream. A different approach is presented in [Reference Reibman, Vaishampayan and Sermadevi59], where the channel distortion affecting the received video sequence is computed according to three different strategies. A first solution computes the final video quality from the network statistics; a second solution employs the packet loss statistics and evaluates the spatial and temporal impact of losses on the final sequence; the third one evaluates the effects of error propagation on the sequence. These solutions target control systems employed by network service providers, which need to monitor the quality of the final video sequences without having access to the original signal. Another no-reference PSNR estimation strategy is proposed in [Reference Naccari, Tagliasacchi and Tubaro60]. The proposed solution evaluates the effects of temporal and spatial error concealment without having access to the original video sequence, and the output values present a good correlation with MOS scores. As a matter of fact, it is possible to consider this approach as a hybrid solution, in that it exploits both the received bitstream and the reconstructed pixel values.
A second class of strategies assumes that the transmitted video sequence has been decoded and that only the reconstructed pixels are available. This situation is representative of all those cases in which the video analyst does not have access to the bitstream. The solution proposed in [Reference Valenzise, Magni, Tagliasacchi and Tubaro61] builds on top of the metrics proposed in [Reference Naccari, Tagliasacchi and Tubaro60], but no-reference quality estimation is carried out without considering the availability of the bitstream. Therefore, the proposed solution processes only pixel values, identifying which video slices were lost, and producing as output a quality value that presents good correlation with the MSE value obtained in full reference fashion. The method assumes that slices correspond to rows of macroblocks. However, modern video coding standard enable more flexible slicing schemes. Hence, the method has been recently extended in [Reference Valenzise, Magni, Tagliasacchi and Tubaro62], in which a maximum a posteriori approach is devised to take into account a spatial prior on the distribution of lost slices.
D) Video compression anti-forensics
The design of novel forensic strategies aimed at characterizing image and video compression is paralleled by the investigation of corresponding anti-forensic methods. That is, a malicious adversary might tamper with video content in such a way to disguise its traces.
An anti-forensic approach for JPEG compression has been recently proposed in [Reference Stamm, Tjoa, Lin and Liu63]. There, the traces of compression are hidden by adding a dithering noise signal. Dithering is devised to reshape the histogram of DCT coefficients in such a way that the original Laplacian distribution is restored. In a following work by the same authors [Reference Stamm, Tjoa, Lin and Liu64], a similar strategy is proposed to erase the traces of tampering from an image and hide double JPEG compression. This is achieved by a combined strategy, i.e., removing blocking artifacts by means of median filtering and restoring the original distribution of DCT coefficients with the same method as in [Reference Stamm, Tjoa, Lin and Liu63]. In this way, the forensic analyst is not able to identify the tampered region by inspecting the distribution of DCT coefficients. However, it has been recently shown that anti-forensic methods are prone to leave their own footprints. In [Reference Valenzise, Tagliasacchi and Tubaro65,Reference Valenzise, Nobile, Tagliasacchi, Tubaro, Macq and Schelkens66], the authors study the distortion which is inevitably introduced by the anti-forensic method in [Reference Stamm, Tjoa, Lin and Liu63] and propose an effective algorithm to counter it.
The aforementioned anti-forensic methods might be potentially applied to videos on a frame-by-frame basis. To the authors' knowledge, the only work that addresses an anti-forensic method specifically tailored to video compression is [Reference Stamm and Liu67]. There, the authors propose a method to fool the state-of-the-art frame deletion and detection technique in [Reference Wang, Farid, Voloshynovskiy, Dittmann and Fridrich4], which is based on the analysis of the motion-compensated prediction error sequence. However, this is achieved by paying a cost in terms of coding efficiency, since some of the frames of the video sequence need to be re-encoded at a bitrate higher than the one originally used. However, this research field is quite recent and just a few works can be found on the subject.
V. FORENSIC TOOLS FOR VIDEO DOCTORING DETECTION
Although being more complicated than for images, creating a forged video is now easier than before, due to the availability of video editing suites. At the same time, videos are extensively used for surveillance, and they are usually considered a much stronger proof than a single shot. There are many different ways of tampering with a video, and some of them are not complicated at all: one may be interested in replacing or removing some frames (e.g. from a video-surveillance recording), replicating a set of frames, introducing, duplicating, or removing some objects from the scene.
It is possible to classify both video forgery and video forensic techniques as intra-frame (attack/analysis is performed frame-wise, considering one frame at a time), or inter-frame (relationships between adjacent frames are considered). Although it would be possible to analyze the integrity of a video by simply applying image forensic tools to each separate frame, this approach is considered unpractical, mainly for these reasons:
• complexity: tools for detecting forgeries in images are usually computationally demanding;
• reliability: replication/deletion of frames would not be detected by any image forensic tools;
• convenience: creating doctored videos that are temporally consistent is very difficult, so these kinds of inter-frame relationships are a valuable asset for forgery identification.
In the following subsections we survey existing techniques for video doctoring detection. We group them according to the type of analysis they rely on. Section V(A) covers camera-based techniques. Section V(B) covers coding-based techniques and Section V(C) discusses some pioneering works that exploit geometrical/physical inconsistencies to detect tampering. In Section V(D), we analyze the problem of identifying frames, or portion of frames, copy-move forgeries. In Section V(E), we discuss anti-forensic strategies. Finally, in Section V(F) we present a solution to the problem of understanding the relationships between objects in large multimedia collections (phylogeny).
A) Camera-based editing detection
As discussed in Section III, camcorders usually leave a characteristic fingerprint in recorded videos. Although these kinds of artifacts are usually exploited just for device identification, some works leverage on them also for tampering detection. The main contributions in this field are from Mondaini et al.[Reference Mondaini, Caldelli, Piva, Barni, Cappellini, E. J. D. III and Wong68], Hsu et al. [Reference Hsu, Hung, Lin and Hsu69], and Kobayashi et al. [Reference Kobayashi, Okabe and Sato70].
Mondaini et al. [Reference Mondaini, Caldelli, Piva, Barni, Cappellini, E. J. D. III and Wong68] proposed a direct application of the PRNU fingerprinting technique (see Section III. A(1) to video sequences: the characteristic pattern of the camcorder is estimated on the first frames of the video, and is used to detect several kinds of attacks. Specifically, authors evaluate three correlations coefficient (see equation 4)): (i) the one between each frame noise and the reference noise, (ii) the one between the noise of two consecutive frames, and (iii) the one between frames (without noise extraction). Each of these correlation coefficients is thresholded to obtain a binary event, and different combinations of events allow to detect different kind of doctoring, among which: frame insertion, object insertion within a frame (cut-and-paste attack), frame replication. Experiments are carried both on uncompressed and on MPEG compressed videos: results show that the method is reliable (only some case studies are reported, not averaged values) on uncompressed videos, while MPEG encoding afflicts performances significantly.
Hsu et al. [Reference Hsu, Hung, Lin and Hsu69] adopt a technique based on temporal correlation of noise residues, where the “noise residue” of a frame is defined as what remains after subtracting from the frame its denoised version (the filtering technique proposed in [Reference Kivanc Mihcak, Kozintsev and Ramchandran39] is used). Each frame is divided into blocks, and the correlation between the noise residue of temporally neighboring blocks (i.e. blocks in the same position belonging to two adjacent frames) are evaluated. When a region is forged, the correlation value between temporal noise residues will be radically changed: it will be decreased if pixels of the blocks are pasted from another frame/region (or automatically generated through inpainting), while it will be raised to 1 if a frame replication occurs. Authors propose a two-step detection approach to lower the complexity of the scheme: first a rough threshold decision is applied to correlations and, if the frame contains a significant number of suspect blocks, a more deep statistical analysis is performed, modeling the behavior of noise residue correlation through a Gaussian mixture and estimating its parameters. Performances are far from ideal: when working on copy-paste attacked videos, on average only 55% of forged blocks are detected (false positive rate being 3.3%); when working on synthetically inpainted frames, detection raises to 74% but also false positive rate increases to 7% on average. Furthermore, when the video is lossy encoded, performances drop rapidly with the quantization strength. Nevertheless, despite authors do not provide experiments in this direction, this method should be effective for detecting frame replication, which is an important attack in the video-surveillance scenario. It is worth noting that, although exploiting camera characteristics, this work does not target the fingerprinting of the device at all.
Another camera-based approach is the one from Kobayashi et al. [Reference Kobayashi, Okabe and Sato70]: they propose to detect suspicious regions in video recorded from a static scene by using noise characteristics of the acquisition device. Specifically, photon shot noiseFootnote 2 is exploited, which mainly depends on irradiance through a function named noise level function (NLF). The method computes the probability of forgery for each pixel by checking the consistency of the NLFs in forged regions and unforged regions. Since it is not known a priori which pixels belong to which region, the EM [Reference Dempster, Laird and Rubin71] algorithm is employed to simultaneously estimate the NLF for each video source and the probability of forgery for each pixel. The core of the technique resides in correctly estimating the function from temporal fluctuations of pixel values, and this estimate is thoroughly discussed from a theoretical point of view. On the other hand, from a practical point of view, the estimate can be performed only for pixels whose temporal variation results entirely from noise and not from motion of objects or camera. This limits the applicability of the approach to stationary videos, like those acquired by steady surveillance cameras. When this assumption is respected, and the video is not compressed, this method yields very good performances (97% of forged pixels are located with 2.5% of false alarm); also, the perfect resolution of the produced forgery map (each pixel is assigned a probability) should be appreciated. Unfortunately, since videos usually undergo some kind of noise reduction during encoding, performances drop dramatically when the video is compressed using conventional codecs like MPEG-2 or H.264, and this further limits the practical applicability of this work.
Going back to a global view, it can be stated that camera-based methods are effective on uncompressed videos. However, videos are typically stored in compressed format in most practical applications. This motivates the investigation of camera footprints that are more robust to aggressive coding.
B) Detection based on coding artifacts
From what emerged in the previous section, video encoding strongly hinders the performances of camera-based detection techniques. On the other hand, however, coding itself introduces artifacts that can be leveraged to investigate the integrity of the content. Since video codecs are designed to achieve strong compression ratios, they usually introduce rather strong artifacts in the content (as seen in Section IV). In the last years, some forensic researchers investigated the presence or the inconsistencies of these artifacts to asses the integrity of a video, and to localize which regions are not original.
The first approach in this direction was from Wang and Farid [Reference Wang, Farid, Voloshynovskiy, Dittmann and Fridrich4], focusing on MPEG compressed videos, where two phenomena are explored, one static (inter-frame) and one temporal (intra-frame). The static phenomena, which has been discussed in Section IV(B), relies on the fact that a forged MPEG video will almost surely undergo two compressions the first being performed when the video is created, and the second when video is re-saved after being doctored. The temporal phenomena are based on the GOP structure of MPEG files. As shown in Fig. 6, when a video is re-compressed after removing or adding a group of frames, a desynchronization will occur in the GOP pattern. Due to the predictive nature of MPEG compression, all the P frames in a GOP are correlated to the initial I frame. In the re-compressed sequence, some of the frames are likely to move from one GOP to another (last row of Fig. 6), so their correlation with the I frame of the new GOP will be smaller, resulting in larger prediction errors. If a single set of frames is deleted, the shift of P frames will be the same throughout all the video sequence, and the variability of prediction error in P frames along time will exhibit a periodic behavior. That is, smaller error values will result for frames that remained in the same GOP as the original video, and larger error for those that changed GOP.

Fig. 6. In this example, the first six frames of the original MPEG compressed video (first row) are deleted, thus obtaining a new sequence (second row). When this sequence is re-compressed using MPEG, each GOP will contain frames that belonged to different GOPs in the original video (frames highlighted in yellow in the third row).
This periodicity can be revealed via a Fourier analysis of the frame-wise average values of motion error. Authors show the effectiveness of this approach on several examples, although they do not allow us to give a value for precision-recall or overall accuracy of the method.
Another work from the same authors [Reference Wang and Farid56] provides a more accurate description of double compression in MPEG videos, which allows them to detect doubly compressed macro-blocks (16 × 16 pixels) instead of frames. Consequently, this approach allows to detect if only part of the frame has been compressed twice, which usually happen when the common digital effect of green screening is applied (that is, a subject is recorded over a uniform background then it is cut and pasted into the target video). Performances of this technique depend on the ratio between the two compression quality factors: for ratios over 1.7 the method is almost ideal (99.4% detection rate) while for ratios less then 1.3 detection drops to 2.5%.
Quantization artifacts are not the only effect that have been exploited for video doctoring detection: Wang and Farid proposed another approach [Reference Wang and Farid72] for detecting tampering in interlaced and de-interlaced video (see Section III. B(1) for a brief explanation of what an interlaced video is). For de-interlaced video, the authors consider how the missing rows of the frame are generated (see Fig. 7 for an example): if they are not tampered with, they should be a combination of fields that are adjacent in time and/or space. Instead, if a region is forged, this relationship should not hold, thus exposing the doctoring. However, in practice, both the adopted interpolation method and the possibly doctored region are not known in advance. The authors propose to exploit the EM algorithm [Reference Dempster, Laird and Rubin71] to simultaneously estimate the parameters of the filter and assign pixels to original or tampered regions. To give a simple example, let us consider the odd rows F o(x, y, t) of an interlaced frame F(x, y, t). Pixels that are not tampered with are said to belong to the model M 1, and should satisfy the following constraint:

where αi and βi are the coefficients of the interpolation filter and n(x, y) is i.i.d. Gaussian noise. On the other hand, pixels in tampered regions belong to another model, M 2, for which a uniform distribution is assumed. With these settings, the EM algorithm iteratively determines the probability of each pixel of F o(x, y, t) to belong to M 1 (expectation step). Then, it uses these assignments to refine the model M 1, by minimizing a cost function expressed in terms of αi and βi (maximization step). Notice that the final result is a pixel-resolution probability map of tampering, and this is an important contribution in that tampering localization is always more difficult than tampering detection.

Fig. 7. Video interpolation based on line averaging, which is a field extension scheme. Compared to the method in Fig. 2, this one has the advantage of producing a final video with T frames instead of T/2, without showing the combing artifact. On the other hand, vertical resolution is halved.
For interlaced video, in which frames are created by simply weaving together the odd and even fields, the presence of rapidly moving objects introduces the combing artifact, already mentioned in Section III. B(1). Since the magnitude of this effect depends on the amount of motion between fields, authors use incoherence between inter-field and inter-frame motion to reveal tampering. Both techniques in [Reference Wang and Farid56] allow the localization of tampering in time (frame) as well in space (region of the frame). Furthermore, both algorithms can be adapted to detect frame rate conversion. Since compression partially removes inter-pixel correlations this approach is mostly suited for medium/high-quality video. For interlaced video, instead, compression does not seem to hinder performance.
We argue that much has still to be discovered in coding-based doctoring detection for videos. As a matter of fact, video coding algorithms are much more complex than JPEG compression. This makes detection of introduced artifacts more difficult, since mathematical models are not easy to derive. However, this should also motivate researchers to look for traces left by such video coding schemes, which are likely to be much stronger compared to the case of images, due to the aggressive compression that it is typically performed.
C) Detection based on inconsistencies in content
As already stated in Section II, it is very difficult to understand whether the geometry or the physical/lighting properties of a scene are consistent. In particular, it is very hard to do so unless some assistance from the analyst is provided. If this effort from the analyst may be affordable when a single image is to be checked, it would be prohibitive to check geometric consistencies in video on a frame-by-frame basis. Existing works usually exploit phenomena connected to motion in order to detect editing. So far, two approaches have been proposed: (i) the one in [Reference Zhang, Su and Zhang73], based on artifacts introduced by video inpainting, (ii) the one in [Reference Conotter, O'Brien and Farid74], that reveals inconsistencies in the motion of objects in free-flight.
Going into details, Zhang et al. [Reference Zhang, Su and Zhang73] propose a method to detect video inpainting, which is a technique that automatically replaces some missing content in a frame by reproducing surrounding textures. Although originally developed for still images, this technique is also applicable frame-by-frame to video signals introducing annoying artifacts, known as “ghost shadows”, due to temporal discontinuity of the inpainted area. Authors observe that these artifacts are well exposed in the accumulative difference image (ADI). This is obtained by comparing a reference image with every subsequent frame and using each pixel as a counter, which is incremented if the current frame differs significantly from the reference image. Unfortunately, ADI would also detect any moving object. Therefore, the authors propose a method to automatically detect the presence of these artifacts, provided that the removed object was a moving object. The authors point out that only detection of forgery is possible, and no localization is provided. Experiments, performed on just a few real world video sequences, show that the method is robust against strong MPEG compression.
Before moving to the work in [Reference Conotter, O'Brien and Farid74], a remark must be made: if detecting geometrical inconsistencies in an inter-frame fashion is difficult, it is perhaps more difficult to detect physical inconsistencies, since this requires to mix together tracking techniques and complex physical models to detect unexpected phenomena. Nevertheless, restricting the analysis to some specific scenarios, it is possible to develop ad hoc techniques capable of such a task. This is what has been done by Conotter et al. in [Reference Conotter, O'Brien and Farid74]: an algorithm is proposed to detect physically implausible trajectories of objects in video sequences. The key idea is to explicitly model the three-dimensional parabolic trajectory of objects in free-flight (e.g. a ball flying towards the basket) and the corresponding two-dimensional projection into the image plane. The flying object is extracted from video, compensating camera motion if needed, then the motion in the 3D space is estimated from 2D frames and compared to a plausible trajectory. If the deviation between observed and expected trajectories is large, the object is classified as tampered. Although analyzing a very specific scenario, the method inherits all the advantages that characterize forensic techniques based on physical and geometrical aspects; for example, performance does not depend on compression and video quality.
D) Copy-move detection in videos
Copy and copy-move attacks on images have been considered in order to prevent the illegal duplication or reusing of images. More precisely, these approaches check for similarities between pairs of images that are not supposed to be related (since they have been taken in different time/places or different origins are claimed). However, it is possible to verify that different images are copies of the same visual content checking the similarity between their features [Reference Kang, Hsu, Chen, Lu, Lin and Pei75]. Many approaches for copy detection in images are based on SIFT, which allows detecting the presence of the same objects in the acquired scene [Reference Kang, Hsu, Chen and Lu76].
Copy-move attacks are defined for video both as intra- and inter-frame techniques. An intra-frame copy-move attack is conceptually identical to the one for still images, and consists in replicating a portion of the frame in the frame itself (the goal is usually to hide or replicate some object). An inter-frame copy-move, instead, consists in replacing some frames with a copy of previous ones, usually to hide something that entered the scene in the original video. To this end, partial inter-frame attacks can be defined, in which only a portion of a group of frames is substituted with the same part coming from a selected frame. To the best of our knowledge, there is only one work authored by Wang and Farid [Reference Wang, Farid, Kundur, Prabhakaran, Dittmann and Fridrich77] that targets copy-move detection directly in video. The method uses a kind of divide-and-conquer approach: the whole video is split in subparts, and different kinds of correlation coefficients are computed in order to highlight similarities between different parts of the sequence. In the same work, a method for detecting region duplication, both for the inter-frame and intra-frame case, is defined. Results are good (accuracy above 90%) for a stationary camera, and still interesting for a moving camera setting (approx. accuracy 80%). MPEG compression does not hinder performance.
E) Anti-forensic strategies
For what concerns video, only a work has been proposed by Stamm and Liu [Reference Stamm and Liu78] to fool one of the forensic techniques described in [Reference Wang, Farid, Voloshynovskiy, Dittmann and Fridrich4] (see Section V(B)), specifically the one based on GOP desynchronization. Authors of [Reference Stamm and Liu78] observe that the simplest way to make the forgery undetectable is to raise prediction errors of all frames to the values assumed in the spikes, so that peaks in the error due to desynchronization will be no longer distinguishable. In order to raise prediction errors, they alter the encoder so that a certain number of motion vectors will be set to zero even if they were not null. The quality of the video will not be reduced, since the error is stored during encoding and compensated before reproduction; furthermore, authors select which vector will be set to zero starting from those that are already small, so that the introduced error is spread on many vectors, and introduced modification is harder to detect. Authors also point out that the other detection technique proposed by Wang et al. in the same work [Reference Wang, Farid, Voloshynovskiy, Dittmann and Fridrich4] can be attacked using counter forensic methods designed for still images, in particular those that hide JPEG quantization effects [Reference Stamm, Tjoa, Lin and Liu79].
For what concerns camera-artifact-based methods, there is a straightforward counter forensic method, which also applies to images: it simply consists in scaling the doctored video (even by a very low factor) and then re-encode it. Since rescaling requires an interpolation step, noise artifacts will be practically erased; furthermore, the correlation operator used in equation (4) is performed element-wise, so frames having different sizes cannot be even compared directly.
F) Video phylogeny
Two videos are termed “near-duplicate” if they share the same content but they show differences in resolution, size, colors, and so on. If we have a set of near duplicate videos, like the one in Fig. 8, it would be interesting to understand whether one of them has been used to generate the others, and draw a graph of causal relationships between all these contents. This problem, which was firstly posed for images under the name “image phylogeny” [Reference Dias, Rocha and Goldenstein80] or “image dependencies” [Reference De Rosa, Uccheddu, Costanzo, Piva and Barni81], is being studied on video under the name of “video phylogeny”. The first (and by now the only) work on video phylogeny is the one by Dias et al. [Reference Dias, Rocha and Goldenstein82].

Fig. 8. An example of near-duplicate frames of the a video.
Given two near-duplicate and frame-synchronized videos V A and V B, given a fixed set ![]() of possible video transformations parameterized by
of possible video transformations parameterized by ![]() , the dissimilarity between V A and V B is defined as
, the dissimilarity between V A and V B is defined as
where L is a comparison method. The best array of parameter ![]() is searched by choosing a set of analogous frames from V A and V B, extracting robust interest points from frames and finding the affine warping between these points. Using this definition of dissimilarity, and for a chosen number f of frames taken from N near-duplicate videos, authors build f dissimilarity matrices, and each of them give the dissimilarity between all couples of videos evaluated on that frame. Instead of directly deriving the video phylogeny tree from these matrices, authors found more convenient to use the image phylogeny approach [Reference Dias, Rocha and Goldenstein80] to build f phylogeny trees, one for each set of frames, and then use a tree reconciliation algorithm that fuses information coming from these trees into the final video phylogeny tree (in our example, the phylogeny tree resulting from Fig. 8 would be as in Fig. 9). Experiments carried by authors show that the method is good (accuracy ~90%) in finding the root of the tree (corresponding to the video originating the whole set) and also correctly classifies leafs 77.7% of the times, but the overall performances in terms of correctly positioned edges are still poor (~65.8%).
is searched by choosing a set of analogous frames from V A and V B, extracting robust interest points from frames and finding the affine warping between these points. Using this definition of dissimilarity, and for a chosen number f of frames taken from N near-duplicate videos, authors build f dissimilarity matrices, and each of them give the dissimilarity between all couples of videos evaluated on that frame. Instead of directly deriving the video phylogeny tree from these matrices, authors found more convenient to use the image phylogeny approach [Reference Dias, Rocha and Goldenstein80] to build f phylogeny trees, one for each set of frames, and then use a tree reconciliation algorithm that fuses information coming from these trees into the final video phylogeny tree (in our example, the phylogeny tree resulting from Fig. 8 would be as in Fig. 9). Experiments carried by authors show that the method is good (accuracy ~90%) in finding the root of the tree (corresponding to the video originating the whole set) and also correctly classifies leafs 77.7% of the times, but the overall performances in terms of correctly positioned edges are still poor (~65.8%).

Fig. 9. The ground-truth phylogeny tree for the near-duplicate set in Fig. 8.
VI. CONCLUSIONS AND FUTURE WORKS
As it has been shown in the previous sections, video forensics is nowadays a hot research issue in the signal processing world opening new problems and investigation threads.
Despite several techniques have been mutuated from image forensics, video signals pose new challenges in the forensic application world because of the amount and the complexity of data to be processed and the wide employment of compression techniques, which may alter or erase footprints left by previous signal modifications.
This paper presented an overview of the state-of-the-art in video forensic techniques, underlying the future trends in this research field. More precisely, it is possible to divide video forensic techniques into three macro-areas concerning the acquisition, the compression, and the editing of the video signals. These three operations can be combined with different orders and iterated multiple times in the generation of the final multimedia signal. Current results show that it is possible to reconstruct simple processing chains (i.e. acquisition followed by compression, double compression, etc.) under the assumption that each processing step does not introduce an excessive amount of distortion on the signal. This proves to be reasonable since a severe deterioration of the quality of the signal would make it useless.
The investigation activity on video forensics is still an ongoing process since the complexity of video editing possibilities requires additional research efforts to make these techniques more robust.
Future research has still to investigate more complex processing chains where each operation on the signal may be iterated multiple times. These scenarios prove to be more realistic since the possibility of transmitting and distributing video content over the internet favors the diffusion of copies of the same multimedia content which has been edited multiple times.
Moreover, anti-forensic and counter-anti-forensic strategies prove to be an interesting issue in order to identify those techniques that could be enacted by a malicious user in order to hide alterations on the signal and how to prevent them.
Future applications will include forensics strategies into existing multimedia applications in order to, e.g., provide the devices with built-in validating functionalities.
ACKNOWLEDGEMENTS
The present work has been developed within the activity of the EU project REWIND (REVerse engineering of audio-VIsual coNtent Data) supported by the Future and Emerging Technologies (FET) programme within the Seventh Framework Programme for Research of the European Commission, under FET-Open grant number: 268478.










