Published online by Cambridge University Press: 17 August 2017
Coming after Muʾayyad al-Dīn al-ʿUrḍī (1200–1266) and Naṣīr al-Dīn al-Ṭūsī (1201–1274), Quṭb al-Dīn al-Shīrāzī (1236–1311), a leading figure of the so-called Marāgha school in astronomy, presents his predecessors’ non-Ptolemaic models and criticizes them in his three hayʾa books. Since his own new models in Nihāyat al-idrāk (written in Arabic in 1281) and Ikhtiyārāt muẓaffarī (written in Persian in 1282) are not without difficulties, in his latest book on hayʾa, al-Tuḥfa al-shāhiyya (written in Arabic in 1285) he puts forward his modified models inspired from Ṭūsī’s and ʿUrḍī’s models and produces a series of new models for Mercury and the oscillation of the spheres. Nevertheless, in spite of all his attempts, the tradition of non-Ptolemaic modeling after him never converged to a series of standard models.
Venu après Muʾayyad al-Dīn al-ʿUrḍī (1200–1266) et Naṣīr al-Dīn al-Ṭūsī (1201–1274), Quṭb al-Dīn al-Shīrāzī (1236–1311), éminente figure de l’école dite de Marāgha en astronomie, présente, dans ses trois ouvrages de hayʾa, les modèles de ses prédécesseurs tout en les critiquant. Puisque ses propres nouveaux modèles, présentés dans Nihāyat al-idrāk (écrit en arabe en 1281) et Ikhtiyārāt muẓaffarī (écrit en persan en 1282), ne sont pas sans difficulté, il présente, dans son dernier ouvrage de hayʾa, al-Tuḥfa al-shāhiyya (écrit en arabe en 1285), d'autres modèles inspirés de ceux d'al-Tūsī et d'al-ʿUrḍī, et produit un ensemble de nouveaux modèles pour Mercure et l'oscillation des sphères. Or, en dépit de tous ces efforts, la tradition des modèles non ptolémaïques, telle qu'elle se développa après lui, ne convergea pas vers un ensemble standard de modèles.
1 A short list of the most important writings are as follows: Kennedy, Edward Stewart, “Late medieval planetary theory”, Isis, 57 (3) (1966): 365–78Google Scholar; Kennedy, Edward S. and Ghanim, ʿImad, The Life & Work of Ibn al-Shāṭir, an Arab Astronomer of the Fourteenth Century (Aleppo, 1976)Google Scholar; Jamil Ragep, “The two versions of the Ṭūsī Couple”, in David King and George Saliba (eds.), From Deferent to Equant: Studies in honor of E. S. Kennedy (1987), pp. 329–56; Ragep, F. Jamil, Naṣīr al-Dīn al-Ṭūsī’s Memoir on Astronomy (al-Tadhkira fī ʿilm al-hayʾa), 2 vols. (New York, 1993)Google Scholar; Saliba, George, History of Arabic Astronomy: Planetary Theories during the Golden Age of Islam (New York, 1995)Google Scholar.
2 The Astronomical Work of Muʾayyad al-Dīn al-ʿUrḍī: A Thirteenth-Century Reform of Ptolemaic Astronomy. Kitāb al-Hayʾah, edition and introduction by Saliba, George (Beirut, 1990)Google Scholar.
3 Ragep, Naṣīr al-Dīn al-Ṭūsī’s Memoir on Astronomy.
4 The most recent one is: Niazi, Kaveh, Quṭb al-Dīn Shīrāzī and the Configuration of the Heavens: A Comparison of Texts and Models (New York, 2014)CrossRefGoogle Scholar.
5 See Gamini, Amir Mohammad and Hamedani, Hossein Masoumi, “Al-Shīrāzī and the empirical origin of Ptolemy's equant in his model of the superior planets”, Arabic Sciences and Philosophy, 23 (2013): 47–67 CrossRefGoogle Scholar.
6 See Ragep, , “Ṭusī and Copernicus: The earth's motion in context”, Science in Context, 14.1-2 (2001): 145–63Google Scholar; Gamini, Amir Mohammad, “A survey of the arguments for the immobility and centricity of the earth in the hayʾa books”, Tarikh-e Elm: Iranian Journal for the History of Science, 11 (2012): 45–80 (in Persian)Google Scholar.
7 See Gamini, Amir Mohammad, “The Venus transit and the order of the planets in Islamic hayʾa works”, Tarikh-e Elm: Iranian Journal for the History of Science, 12 (2012): 41–63 (in Persian)Google Scholar.
8 Ragep, , “Shīrāzī’s Nihāyat al-idrāk: introduction and conclusion”, Tarikh-e-Elm, 11 (2013): 41–57, pp. 45–6Google Scholar.
9 Shīrāzī, Ikhtiyārāt muẓaffarī, MS Tehran, Milli Library, 31402, last page. This colophon indicates that the original manuscript was completed before the morning of ‘Arafa night, which traditionally is known as the holy night 9th of Dhū al-Ḥijja.
10 Minovi, M., “Mulla Quṭb Shīrāzī”, in Yadnameh-i Irani-i Minorsky (Tehran, 1348), pp. 165–205, p. 190Google Scholar; Niazi, Quṭb al-Dīn Shīrāzī, p. 85.
11 It has been attested very well by Niazi (Niazi, Quṭb al-Dīn Shīrāzī, pp. 119–20). He invites the scholars to a deeper exploration of Shīrāzī’s model-building activity, especially in the period 1281–1285 (ibid., p. 121). Here I present more aspects of the story based on my parallel researches, as well as the evolving process of Shīrāzī’s modeling, his critical approach to his predecessors and his new models for Mercury and motion in latitude which was left by Niazi for the future studies.
12 A list of the difficulties of the Ptolemaic models is presented by Ragep referring to Ṭūsī’s Tadhkira (Ragep, Naṣīr al-Dīn al-Ṭūsī’s Memoir on Astronomy, p. 50).
13 Ibn al-Haytham mentions the oscillation of lunar epicycle due to prosneusis point in longitude (Ibn al-Haytham, al-Shukūk ʿalā Baṭlamiyūs, edited by Abdelhamid Sabra [Cairo, 1971], pp. 16–18), the non-uniform motion of the deferent (ibid., p. 27), oscillations of the epicycle in latitude (ibid, p. 36) and the oscillation of the inferior planets’ deferents (ibid., p. 41) as the difficulties of Ptolemaic models. Although he also mentions the oscillation of the five planets’ epicycles due to the equant point in longitude (ibid., p. 28) as a difficulty, this difficulty did not appear in the standard lists of the difficulties and is mentioned by none of the modern scholars. Only Shīrāzī in his Ikhtiyārāt mentions it, claiming, through a geometric demonstration, that it is not a real difficulty for the five planets ( Shīrāzī, , Ikhtiyārāt Muẓaffarī, MS Tehran, Milli Library 11954, p. 96 Google Scholar). For a technical exploration to this argument and its erroneous see my PhD dissertation ( Gamini, Amir Mohammad, Shīrāzī and his Role in Science of Hayʾa, Iranian Institute for Philosophy, Tehran, 2013, pp. 237–40Google Scholar). Although we know that Ikhtiyārāt is completed 4 months after Nihāya, Shīrāzī did not mention this demonstration in Nihāya, referring to Ikhtiyārāt. For a full consideration of this point see Niazi, Quṭb al-Dīn Shīrāzī, pp. 134–5.
14 Ragep, Naṣīr al-Dīn al-Ṭūsī’s Memoir on Astronomy, pp. 99–103, Shīrāzī, Nihāyat al-idrāk fī dirāyat al-aflāk, MS Istanbul, Köprülü Library 957, fols. 7b–8a; Shīrāzī, Ikhtiyārāt, pp. 15–16; Shīrāzī, Al-Tuḥfa al-Shāhiyya, MS Tehran, Majlis Library 3835, p. 10.
15 Saliba wrongly attributes the equant problem to the solidity of the spheres and not to the natural principle of uniform motion of the spheres, because, as he claims, it is “physically impossible that a sphere move uniformly around an axis that did not pass through its center” (Saliba, History of Arabic Astronomy, p. 23). According to Ptolemaic models, what is uniform with respect to the equant point is the motion of the epicycle center, which is a point on the circumference of the deferent, and not, as Saliba supposes, the motion of all the point of its circumference. Therefore it is physically possible to imagine a solid sphere rotating with non-uniform speed in such a manner that a point on its circumference, namely the epicycle center, rotates uniformly with respect to the equant point. This motion is only in contradiction with the Aristotelian natural philosophy, and not with the reality of the solid spheres. Although Sabra explicitly mentions the non-uniformity as the difficulty of Ptolemaic models ( Sabra, Abdelhamid, “Configuring the universe: aporetic, problem solving, and kinematic modeling as themes of Arabic astronomy”, Perspectives on Science, 6.3 [1998]: 288–330, pp. 293, 299Google Scholar), Saliba repeats his wrong understanding in his reply to Sabra ( Saliba, George, “Arabic versus Greek astronomy: a debate over the foundations of science”, Perspectives on Science, 8.4 [2000]: 328–41, p. 331Google Scholar).
16 Ptolemy's Almagest, ed. Toomer, Gerald J. (New York, 1984), pp. 141–53Google Scholar; Claudii Ptolemaei opera quae exstant omnia. Vol. I: Syntaxis mathematica, Pars I, Libros I–VI, ed. Heiberg, Johan L. (Leipzig, 1898), p. 216 Google Scholar.
17 Ragep, Naṣīr al-Dīn al-Ṭūsī’s Memoir on Astronomy, pp. 131–43.
18 Isḥāq ibn Ḥunayn translated υποθέσεων into uṣūl meaning “principles” (Baṭlamiyūs, al-Majisṭī, MS Tunis, National Library 478, fol. 35b). Morrison and Niazi prefer “hypothesis” ( Morrison, Robert, “Quṭb al-Dīn al-Shīrāzī’s hypotheses for celestial motions”, Journal for the History of Arabic Science, XIII (2005): 21–140, p. 23Google Scholar; Niazi, Quṭb al-Dīn Shīrāzī, pp. 98–101), while Ragep suggests “model” (Ragep, Naṣīr al-Dīn al-Ṭūsī’s Memoir on Astronomy, p. 130).
19 Shīrāzī, Nihāya, fols. 33b–41a; al-Tuḥfa, pp. 63–89 (This chapter is edited and translated into English alongside with a commentary by Morrison, “Quṭb al-Dīn al-Shīrāzī’s hypotheses”, pp. 39–140). In Ikhtiyārāt the non-Ptolemaic simple models appear wherever they are needed, not in a separate chapter on simple models (Ikhtiyārāt, pp. 75–88).
20 Ragep, Naṣīr al-Dīn al-Ṭūsī’s Memoir on Astronomy, pp. 195–209.
21 For a description of this sub-model in its linear and curvilinear versions and history of the construction of Ṭūsī Couple in Ṭūsī’s Persian and Arabic works see: Ragep, Jamil, “Persian context of the Ṭūsī Couple”, in Pourjavadi, Nasrollah and Vesel, Živa (eds.), Naṣīr al-Dīn Ṭūsī: Philosophe et savant du XIIIe siècle (Tehran, 2000), pp. 113–30Google Scholar.
22 Ṭūsī’s proof is not without difficulty (Ragep, Naṣīr al-Dīn al-Ṭūsī’s Memoir on Astronomy, p. 446).
23 Ragep and Hartner's calculations do not show a deviation more than 8 minutes for the Moon (Ragep, Naṣīr al-Dīn al-Ṭūsī’s Memoir on Astronomy, pp. 443–5; Hartner, Willy, “Nasir al-Din al-Tusi's lunar theory”, Physis, 11 [1969]: 287–304, pp. 298–9Google Scholar).
24 Shīrāzī, Ikhtiyārāt, p. 160. See also Niazi, Quṭb al-Dīn Shīrāzī, pp. 132–4.
25 See Aristotle's On the Heavens, ed. Guthrie, William K. C. (Cambridge, Mass., 1939), 288a–290b Google Scholar. Ibn Sīnā, following Aristotle's Physics (262a), explores if there is a station between back and forth motion (Ibn Sīnā, Al-Shifāʾ: al-Ṭabīʿiyyāt, edited by Ibrāhīm Madkūr [Qom, 1405 A.H.], vol. 1, p. 292).
26 Shīrāzī, Nihāya, fol. 49a; Shīrāzī, Ikhtiyārāt, pp. 132–3.
27 We quote from Morrison, “Quṭb al-Dīn al-Shīrāzī’s hypotheses”, p. 114–15, with some modification. I think Morison wrongly translates kaʿb (کعب) into “cube” and khayṭ (خيط) into “line”. This leads him to draw a figure which makes no sense (pp. 58–9, 91).
28 The Astronomical Work of al-ʿUrḍī, ed. Saliba, pp. 55, 220.
29 Saliba, “Arabic planetary theories after the eleventh century AD”, in Rashed, Roshdi (ed.), Encyclopedia of the History of Arabic Science, 3 vols. (London, 1996), vol. 1, p. 106CrossRefGoogle Scholar.
30 Shīrāzī, Nihāya, fols. 38b, 59a; Ikhtiyārāt, pp. 111–12. Shīrāzī does not present this model in the abstract form of ʿUrḍī Lemma in his Nihāya and Ikhtiyārāt, but only in the Tuḥfa (Morrison, “Quṭb al-Dīn al-Shīrāzī’s hypotheses”, p. 121).
31 Shīrāzī, Ikhtiyārāt, p. 160. See Niazi, Quṭb al-Dīn Shīrāzī, pp. 132–4.
32 See Sabra, Abdelhamid, “Ibn Haytham's treatise: Solution of difficulties concerning the movement of iltifāf”, Journal for the History of Arabic Science, 3 (1979): 388–422 Google Scholar; Ragep, “Ibn al-Haytham and Eudoxus: the revival of homocentric modeling in Islam”, in Hogendijk, Jan P., Burnett, Charles, Plofker, Kim, and Yano, Michio (eds.), Studies in the History of the Exact Sciences in Honour of David Pingree (Leiden, 2004), pp. 786–809 Google Scholar.
33 Ragep, “Ibn al-Haytham and Eudoxus”, pp. 794–9; Ragep, Naṣīr al-Dīn al-Ṭūsī’s Memoir on Astronomy, pp. 215–17.
34 Rajep, “The two versions of the Ṭūsī Couple”.
35 Saliba, George and Kennedy, Edward S., “The spherical case of the Ṭūsī Couple”, Arabic Sciences and Philosophy, 1.2 (1991): 285–91CrossRefGoogle Scholar.
36 Ragep, Naṣīr al-Dīn al-Ṭūsī’s Memoir on Astronomy, p. 219; Shīrāzī, Nihāya, fol. 41a; Ikhtiyārāt, p. 186; Tuḥfa (Morrison, “Quṭb al-Dīn al-Shīrāzī’s hypotheses”, p. 113).
37 Saliba and Kennedy, “The spherical case”, p. 108; Ragep, Naṣīr al-Dīn al-Ṭūsī’s Memoir on Astronomy, p. 361.
38 Morrison, “Quṭb al-Dīn al-Shīrāzī’s hypotheses”, p. 96. Morrison calculates this deviation for 1 degree oscillation and obtains only 0.001 degrees (p. 95).
39 Saliba and Kennedy, “The spherical case”, p. 111. They calculate this deviation for a Ṭūsī couple whose small circle is 60 units and obtain only 3 units. None of commentators obtain a value for this deviation.
40 Shīrāzī, Nihāya, fol. 71b; Ikhtiyārāt, pp. 198–9.
41 Ragep, Naṣīr al-Dīn al-Ṭūsī’s Memoir on Astronomy, pp. 205, 438–41.
42 Ibid ., pp. 209, 446.
43 Ibid ., p. 209.
44 Nihāya, fol. 58b:

45 For a detailed description of this issue see Ragep, “The two versions”, p. 339.
46 The Astronomical Work of al-ʿUrḍī, ed. Saliba, pp. 221–7; Saliba, “Arabic planetary theories”, pp. 105–8.
47 See Gamini and Masoumi Hamedani, “Al-Shīrāzī and the empirical origin”. This argument is absent from Ikhtiyārāt (Niazi, Quṭb al-Dīn Shīrāzī, pp. 129–30).
48 Shīrāzī, Ikhtiyārāt, pp. 136–7:

49 Shīrāzī, Nihāya, fol. 53b; Ikhtiyārāt, p. 137.
50 The Astronomical Work of al-ʿUrḍī, ed. Saliba, p. 251; Saliba, “Arabic planetary theories”, p. 115–17.
51 The reason behind the ʿUrḍī’s model for Mercury has never been discussed by the modern scholars.
52 Shīrāzī, Ikhtiyārāt, p. 177:

53 Shīrāzī, Nihāya, fols. 73a–81b.
54 In the introduction of Ikhtiyārāt, Shīrāzī states that people had difficulties with Nihāya to distinguish his “selected theories” (Madhhab-i Mukhtār) from other models (p. 2). I think this phrase explains the reason behind the name of “Ikhtiyārāt” which means “selections” referring to his distinguishable selected models presented appropriately in Ikhtiyārāt, contrary to Niazi (Quṭb al-Dīn Shīrāzī, p. 9, n. 42), who relates the name to the astrological traditions.
55 Shīrāzī, Nihāya, fols. 37b–38b, 59a; Ikhtiyārāt, pp. 142–4.
56 Shīrāzī, Ikhtiyārāt, p. 160.
57 Thus Shīrāzī calls this book, while Saliba calls it Kayfiyyat tarkīb al-aflāk and Ragep calls it Khilāṣ kayfīyyat tarkīb al-aflāk (Ragep, “The Khilāṣ kayfīyyat tarkīb al-aflāk of al-Jūzjānī: a preliminary description of its Avicennian themes”, in Langermann, Tzvi [ed.], Avicenna and his Legacy: A Golden Age of Science and Philosophy [Turnhout, 2009], pp. 301–6Google Scholar.)
58 See Saliba, , “Ibn Sīnā and Abū ‘Ubayd al-Jūzjānī: the problem of the Ptolemaic equant”, Journal for the History of Arabic Science, 4.2 (1980): 376–87Google Scholar.
59 Jūzjānī writes as follows (Saliba, History of Arabic Astronomy, pp. 92, 104):

60 Shīrāzī, Nihāya, fol. 38b; Ikhtiyārāt, p. 144.
61 Ragep reads fa‘alta meaning “you have done”, nevertheless the copyist of MS Majlis added a ḍamma (فعلتُ) which makes it read fa‘altu meaning “I have done” (Shīrāzī, Fa‘altu fa-lā talum, MS Teheran, Majlis Library, 3945 [previously listed as 3944], fol. 13b). This manuscript is claimed to have been copied from the author's own handwriting.
62 Shīrāzī, Fa‘altu, fol. 64b; Saliba, History of Arabic Astronomy, p. 89.
63 Morrison, “Quṭb al-Dīn al-Shīrāzī’s hypotheses”, p. 133.
64 E.g. see Nihāya, fol. 38b.
65 Shīrāzī, Nihāya, fol. 73a; Ikhtiyārāt, p. 184. Although this model is not presented separately in al-Tuḥfa, it is employed in planetary models.
66 Shīrāzī, Nihāya, fol. 78b; Ikhtiyārāt, pp. 147–51.
67 Nihāya, fol.78b:
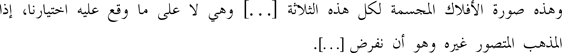
This phrase continues with an abridged description of Tuḥfa model for the superiors without any figure.
68 Shīrāzī, Nihāya, MS Tabriz Library 56, fol. 123a (with many thanks to Mr Hadi Tabataba'i). This manuscript is without any sign of a revision and seems to be the first version of Nihāya, nevertheless it contains the reference to Ikhtiyārāt (see note 13) in the text body (fol. 89a).
69 Shīrāzī, Nihāya, MSS Istanbul, Köprülü Library, 956, fol. 78b; Köprülü Library, 957, fol. 98b; Tehran, Malik Library, 3506, fol. 108b.
70 Niazi draws the same conclusion based on Köprülü manuscripts (Niazi, Quṭb al-Dīn Shīrāzī, pp. 117–18).
71 This model had been attributed by Kennedy to Shīrāzī (Kennedy, “Late medieval”, pp. 371–3) and after a while its original author was found ( Saliba, , “The original source of Quṭb al-Dīn al-Shīrāzī’s planetary model”, Journal for the History of Arabic Science, 3.1 [1979]: 3–18 Google Scholar).
72 Shīrāzī, Tuḥfa, pp. 120–5.
73 Shīrāzī, Nihāya, fol. 77a-b; Ikhtiyārāt, pp. 116–20.
74 Nihāya, MS Köprülü 956, fol.77b:
وهذه صورة أفلاکه لا علی المذهب المختار للاستغناء عن الحافظة.
75 See note 13.
76 Dallal, Ahmad, “A non-Ptolemaic lunar model from fourteenth century central Asia”, Arabic Sciences and Philosophy, 2.2 (1992): 237–98, pp. 237–43CrossRefGoogle Scholar.
77 Ragep, Naṣīr al-Dīn al-Ṭūsī’s Memoir on Astronomy, p. 208.
78 Shīrāzī, Nihāya, fol. 65b. This model is not repeated in Ikhtiyārāt.
79 Shīrāzī, Nihāya, fols. 80a–81a; Ikhtiyārāt, pp. 165–8.
80 Nihāya, fol. 80b:
![]()
81 Ikhtiyārāt, p. 178.
82 Quran 27:16.
83 Ikhtiyārāt, p. 178:

84 Ikhtiyārāt, p. 178.
85 Tuḥfa, p. 178.
86 Tuḥfa, pp. 156–62.
87 Kennedy, “Late medieval”, pp. 373–5.
88 Tuḥfa, p. 183.
89 Tuḥfa, pp. 136–7.
90 Khafrī, Ṣadr al-Sharī‘a, Qūshjī and Ibn al-Shāṭir are the known ones.
91 Bagheri, Mohammad, From Samarqand to Kashan: Letters of Kāshānī to his Father (Tehran, 1375 H.), p. 66 Google Scholar.
92 Brentjes, Sonja, “The mathematical sciences in the Safavid empire: questions and perspectives”, in Hermann, Denis and Speziale, Fabrizio (eds.), Muslim Cultures in the Indo-Iranian World during the Early-Modern and Modern Periods (Berlin, 2010), pp. 325–402 Google Scholar, pp. 331, 343, 345, 346 and 359.
93 There is no known non-Ptolemaic model of him now.
94 Hossein Masoumi Hamedani, “A book to prove the modern astronomy”, Maʿaref, 2 (1363 H./1984): 117–85, p. 162.