The 2000 Centers for Disease Control and Prevention (CDC) growth charts(Reference Kuczmarski, Ogden and Guo1, Reference Ogden, Kuczmarski and Flegal2) are widely used to standardise BMI for differences by sex and age. The charts consist of ten BMI percentiles from the 3rd to the 97th, estimated using various smoothing methods(Reference Kuczmarski, Ogden and Guo1, Reference Flegal and Cole3). Overweight is classified as BMI ≥ 85th percentile for a child’s sex and age, while obesity is a BMI ≥ 95th percentile of these growth charts(Reference Ogden and Flegal4).
These percentiles were subsequently used to derive the three age-specific parameters needed for the LMS method(Reference Flegal and Cole3, Reference Cole5, Reference Cole and Green6): L (power transformation for normality), M (median) and S (generalised CV). This allows one to calculate the sex-specific BMI-for-age z (BMIz) score and the corresponding percentile for any child. BMIz score has been widely used in cross-sectional and longitudinal analyses where BMI is treated as a continuous variable, including those evaluating the efficacy of interventions among children with very high BMI. Continuous variables are best analysed as continuous rather than dichotomised(Reference Ragland7, Reference Royston, Altman and Sauerbrei8), but there are several limitations of the BMIz score based on the CDC growth charts.
Because the BMI distribution in childhood in the USA is very skewed, transforming it to BMIz shrinks the scale at the upper end. The degree of skewness shows itself in the L parameter, the BMI power transformation, being far smaller than 1 (where 1 indicates no transformation) and between −2 and −3 at most ages. These low values of the L parameter lead to the upper tail of the BMI distribution that is compressed into a narrow z score range at most ages(Reference Freedman, Butte and Taveras9, Reference Freedman, Butte and Taveras10) and an upper limit for BMIz that varies substantially by age and sex(Reference Woo11). This compression can result in similarly aged children with markedly different BMIs having similar z scores. Further, because the maximum value of BMIz in the CDC growth charts differs by sex and age, it is possible for (say) the BMI of a 2-year-old girl to increase substantially over the next 2 years, but her BMIz decreases by more than 1 standard deviation(Reference Freedman, Butte and Taveras12). Similar limitations have also been noted for BMIz based on other growth charts constructed using the LMS method(Reference Woo11, Reference Júlíusson, Roelants and Benestad13). A further problem with the CDC charts is that high z scores do not correspond well with the observed data(Reference Flegal, Wei and Ogden14) as they were estimated from data between the 3rd and the 97th percentiles. Severe obesity is classified as a BMI ≥ 120 % of the CDC 95th percentile.
These limitations have resulted in various alternatives being proposed for analyses with BMI as a continuous variable. They include focusing on changes in BMI rather than in BMIz in longitudinal analyses(Reference Berkey and Colditz15, Reference Cole, Faith and Pietrobelli16), expressing a child’s BMI as a percentage of the 95th percentile (%BMIp95)(Reference Freedman, Butte and Taveras9, Reference Freedman, Butte and Taveras10, Reference Flegal, Wei and Ogden14, Reference Gulati, Kaplan and Daniels17) and using a modified z score that extrapolates a fixed sd outwards(Reference Chambers, Tanamas and Clark18). Although these metrics avoid the compression of very high BMIs into a narrow range of z scores, it is unclear whether they are useful for lower BMIs and whether they convey similar information across ages. Furthermore, they are tied to the CDC growth charts at only one point (the 95th percentile for %BMIp95) or two points (the median and a z score of ±2 for the modified z score(19)).
It is possible, however, to create other BMI metrics that are more strongly linked to the CDC growth charts and which, unlike %BMIp95, use the more robust estimate of the median. In the LMS transformation, for example, L can be set to a fixed value less extreme than −2 or −3, such as 1 (corresponding to no transformation), 0 (log transformation) or another constant, while retaining the M and S parameters. This leads to a modified metric that can be interpreted as either absolute distance (kg/m2) or % distance from the median, avoiding the compression of very high BMIs into a narrow z score range. Further, knowing a child’s distance or % distance from the median may be more interpretable than knowing their modified z score or %BMIp95. Expressing BMI as a % distance from the median is similar to expressing a child’s weight as a percentage of the median (standard) weight, a metric that predates the use of z scores and centiles(Reference Waterlow20, Reference Gomez, Galvan and Frenk21).
Our objective is to evaluate the performance of three alternative metrics to BMIz based on setting L equal to 1 or 0. These two L values result in metrics that are interpretable as the distance of BMI from the median in absolute (kg/m2) and proportional (%) terms, with the latter calculated on both linear and log scales. Thus, the three metrics are (1) absolute distance from the median, (2) % distance from the median and (3) % distance from the median on a log scale. We show how these metrics are related to the LMS transformation and then examine the tracking of these metrics over time and the effects of age adjustment. Because of the well-documented poor tracking of BMIz among children with severe obesity(Reference Freedman, Butte and Taveras12, Reference Freedman and Berenson22), we do not emphasise comparisons with this metric. The new metrics can be used in conjunction with the current cut points for overweight (BMI between the 85th and 94th percentiles of the CDC growth charts) and obesity (BMI ≥ 95th percentile).
Subjects and methods
Study sample
The Bogalusa Heart Study examined the development of risk factors for CVD(Reference Berenson, McMahan and Voors23). Seven cross-sectional studies of schoolchildren were conducted from 1973–1974 through 1992–1994, with each examining about 3500 children. Children of pre-school age (n 714) were also examined in 1973–1974. We also used information from 640 participants of 18- and 19-year-olds who were examined in various studies during this period(Reference Webber, Cresanta and Croft24). All procedures were approved by ethics committees at Louisiana State University Medical Center and Tulane School of Public Health. Parental permission and assent of the child were obtained prior to participation, and informed consent was obtained for participation as an adult. The present study is a secondary analysis of these data.
Altogether these studies involved 27 212 examinations among 11 665 participants of 2- to 19-year-olds. As previously described(Reference Freedman, Lawman and Galuska25), we excluded data thought to be biologically implausible(26) or inconsistent across examinations. To focus on tracking through childhood, we restricted the analysis to children who were examined twice or more, with the first visit occurring before age 12 years. This was because the value of S varies substantially with age before age 12 years but is relatively constant among older children(Reference Freedman, Butte and Taveras10, 27); and if S is constant, age adjustment will not influence % distance on either the linear or log scale. These exclusions resulted in a sample of 5628 children with 18 381 measurements, mean 6·8 years from first to last measurement.
BMI metrics
Height was measured to the nearest 0·1 cm and weight to the nearest 0·1 kg; BMI was calculated as kg/m2. BMIz was calculated using the sex-age-specific values of L, M, and S (Reference Cole5, Reference Cole and Green6) in the CDC growth charts(Reference Kuczmarski, Ogden and Guo1, 26).
If the value of L is set at 1 or 0, the LMS transformation can be interpreted as either the distance (kg/m2) or % distance from the median (on a linear or logarithmic scale). When L = 1 (i.e. untransformed BMI) equation (1) can be multiplied by M/M to yield
Multiplication of both the numerator and denominator of equation (2) by 100/M yields
where the subscript 1 in BMIz1 indicates L = 1. Similarly, when L = 0 (corresponding to log BMI) equation (1) can be written as
Formulas 2 through 4 are alternative z scores; note that M × S in equation (2) corresponds to the age-specific sd. If equation (2) is multiplied by M × S, BMI is expressed as absolute distance (kg/m2) from the median. Similarly if equations (3) and (4) are multiplied by 100 × S, they express BMI as the % distance from the median; equation (4) expresses it on a logarithmic scale resulting in symmetrical and equal percentages(Reference Cole and Altman28). To illustrate equation (3) v. (4), consider two girls, one whose BMI is twice the median and the other whose BMI is half the median. Using equation (3) their distances from the median are +100 % and –50 %, while with equation (4) their distances are +69 % and −69 %.
Thus equations (2) to (4) measure the distance from the median as respectively
and
It follows that equations (2)–(4), as forms of z score, are measures of BMI distance from the median scaled by M and/or S. But M and S vary by age, so the relevance of the distance also varies by age. To address this, equations (2)–(4) can be multiplied by values of M and/or S for some reference age, say M ref and S ref, which is equivalent to scaling equations (5)–(7) as follows:
and
In this analysis we use a reference age of 20 years, but if desired, a different reference age could be used for values of M ref and S ref. Note that equations (8)–(10) are equivalent to equations (2)–(4) multiplied by either ![]() ${M_{{\rm{ref}}}} \times {S_{{\rm{ref}}}}$ or S ref, so not only are they age-adjusted metrics, they are also scaled z scores.
${M_{{\rm{ref}}}} \times {S_{{\rm{ref}}}}$ or S ref, so not only are they age-adjusted metrics, they are also scaled z scores.
To illustrate the metrics, we consider three girls of different ages whose BMI is 140 % of the 95th percentile(Reference Flegal, Wei and Ogden14, Reference Gulati, Kaplan and Daniels17) (Table 1). For the 3-year-old, her BMI of 25·6 is a distance of 9·9 kg/m2 above her age-sex-specific median. Adjusted to age 20 years, her distance is ![]() $9\!\cdot\!9 \times {{\left( {21\cdot7 \times 0\cdot153} \right)} \over {\left( {15\cdot7 \times 0\cdot079} \right)}} = 26\!\cdot\!5\,{\rm{kg}}/{{\rm{m}}^2}$ from the age-20 median, from equation (8). This adjustment scales the +9·9 kg/m2 distance to the comparable distance at the reference age of 20 years when the BMI distribution is more variable. Similarly, from equations (6) and (9), her BMI as % distance from the median is
$9\!\cdot\!9 \times {{\left( {21\cdot7 \times 0\cdot153} \right)} \over {\left( {15\cdot7 \times 0\cdot079} \right)}} = 26\!\cdot\!5\,{\rm{kg}}/{{\rm{m}}^2}$ from the age-20 median, from equation (8). This adjustment scales the +9·9 kg/m2 distance to the comparable distance at the reference age of 20 years when the BMI distribution is more variable. Similarly, from equations (6) and (9), her BMI as % distance from the median is ![]() $\left( {100 \times 25\!\cdot\!6/15\!\cdot\!7} \right) - 100 = 63\,{\rm{\% }}$ unadjusted, or
$\left( {100 \times 25\!\cdot\!6/15\!\cdot\!7} \right) - 100 = 63\,{\rm{\% }}$ unadjusted, or ![]() $63\,{\rm{\% }} \times 0\!\cdot\!153/0\!\cdot\!079 = 122\,% $ adjusted. Finally, her % distance from the median on the log scale, from equations (7) and (10), is
$63\,{\rm{\% }} \times 0\!\cdot\!153/0\!\cdot\!079 = 122\,% $ adjusted. Finally, her % distance from the median on the log scale, from equations (7) and (10), is ![]() $100 \times {\rm{log}}\left( {25\!\cdot\!6/15\!\cdot\!7} \right) = 49\,{\rm{\% }}$ unadjusted, and
$100 \times {\rm{log}}\left( {25\!\cdot\!6/15\!\cdot\!7} \right) = 49\,{\rm{\% }}$ unadjusted, and ![]() $49\,{\rm{\% }} \times 0\!\cdot\!153/0\!\cdot\!079 = 95\,{\rm{\% }}$ adjusted. In general, for high BMI a child’s % distance, whether unadjusted or adjusted, is about 20–30 % lower when calculated on the log v. linear scale.
$49\,{\rm{\% }} \times 0\!\cdot\!153/0\!\cdot\!079 = 95\,{\rm{\% }}$ adjusted. In general, for high BMI a child’s % distance, whether unadjusted or adjusted, is about 20–30 % lower when calculated on the log v. linear scale.
Table 1. Examples of unadjusted v. age-adjusted BMI metrics among girls with a BMI that is 140 % of the 95th percentile

M, median; S, generalised CV.
* M and S are rounded from the tabulated values. The adjusted metrics are scaled to the BMI distribution at age 20 years using the values of M and/or S.
Fig. 1 focuses on three girls whose BMI tracks at 60, 110 and 160 % distance from the median. Fig. 1(a) compares unadjusted (dashed lines) and adjusted (solid lines) % from the median, while Fig. 1(b) shows BMIz. On the BMI scale (a) the unadjusted curves are fairly equally spaced at all ages, while the adjusted curves, which account for differences in the dispersion of BMI by age, are closer together at younger ages. At age 2 years, for example, BMI on the top 160 % curve is about thirty adjusted but much higher at forty-three unadjusted. On the BMIz scale (b) the upper two curves are much closer together than the lower two, and this effect becomes more marked with increasing BMIz. The three dots in the left panel represent the examples in Table 1, BMIs that are 140 % of the 95th percentile at ages 3, 10 and 18 years, and they are all close to 110 % adjusted distance. However, the corresponding unadjusted % distances vary substantially (63–100 %, Table 1), showing the difficulty in comparing unadjusted % distance across a wide age range.
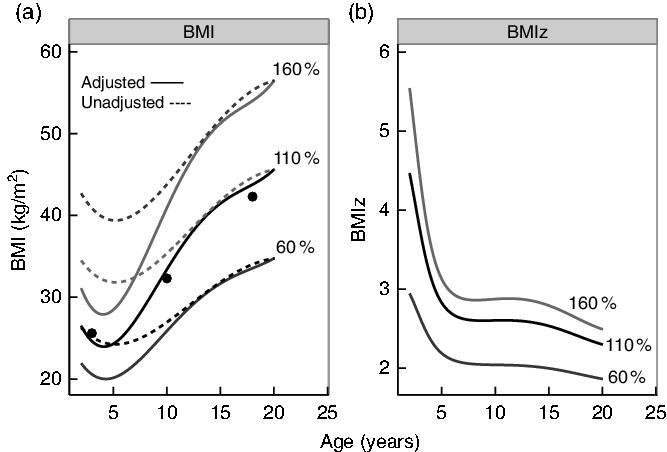
Fig. 1. BMI (a) and BMI z score (BMIz) (b) by age for girls who had adjusted BMI distances (solid lines) from the median of 60, 110 and 160 %. These values correspond to BMIs of approximately 35, 45 and 55 kg/m2 at age 20 years. The dashed lines in (a) represent the corresponding unadjusted % distance. The three points in the left panel represent the BMIs of a girl at age 3, 10 and 18 years who has a BMI that is 140 % of the 95th percentile.
Statistical methods
The unadjusted and age-adjusted versions of the three BMI metrics are called distance from the median (5) and (8), % from the median (6) and (9), and log % from the median (7) and (10). The metrics are compared on the basis of how well they tracked over time within individuals, using the intraclass correlation coefficient (ICC) as a measure of repeatability(Reference Nickerson29, Reference McGraw and Wong30). One property of a good BMI metric is that it should not change materially with age, so that values can be compared between younger and older children.
In contrast to the Pearson correlation, the ICC focuses on within-child clustering, contrasting the between-child and within-child variances. For example, if two girls had BMI of 20 and 25 kg/m2 initially, and both BMIs increased by 4 kg/m2 upon re-examination, the Pearson correlation would be 1. The ICC, however, accounts for the 4 kg/m2 difference between examinations and can be estimated from a one-way ANOVA using the mean square between children, 2 × variance ![]() $\left( {{{20 + 24} \over 2},{{25 + 29} \over 2}} \right) = 25$, and mean square (error) within children,
$\left( {{{20 + 24} \over 2},{{25 + 29} \over 2}} \right) = 25$, and mean square (error) within children, ![]() $0\!\cdot\!5 \times \left( {4 \times {2^2}} \right) = 8$; the ICC would be
$0\!\cdot\!5 \times \left( {4 \times {2^2}} \right) = 8$; the ICC would be ![]() ${{25-8} \over {25 + 8}} = 0\!\cdot\!52$. A higher ICC (maximum 1·0) indicates greater tracking (repeatability) over time.
${{25-8} \over {25 + 8}} = 0\!\cdot\!52$. A higher ICC (maximum 1·0) indicates greater tracking (repeatability) over time.
ICCs for each metric were examined in the overall sample and also stratified by BMI status, age at initial examination and mean time interval between the first and last examination. All analyses were performed in R(31), and the ICCs were calculated from the variance components of mixed-effects models using the lme4 package(Reference Bates, Maechler and Bolker32). This corresponds to a one-way random effects ICC(Reference Nickerson29, Reference McGraw and Wong30). As this is a secondary analysis of a large data set, power calculations were not performed.
Results
Table 2 shows descriptive characteristics at the first and last examination, with mean age of 7·3 and 13·4 years. Mean BMI increased by 4·1 kg/m2 between the examination, and BMIz and the alternative BMI metrics also increased over time, indicating that, on average, children gained BMI faster than indicated by median BMI in the CDC growth charts.
Table 2. Descriptive characteristics among 5628 children with longitudinal data* (Mean values and standard deviations; percentages)

M, median; S, generalised CV.
* The 5628 children had 18 381 examinations altogether; this table is restricted to each child’s first and last examinations.
† Adjusted using the reference values of M and S at age 20 years (Table 1).
Table 3 compares the ICCs for BMIz and the three BMI distance metrics using data from all 18 381 examination (mean, 3·3 per child). Overall, the ICCs for the age-adjusted metrics and BMIz were very similar (0·83–0·84), while those for the unadjusted metrics were slightly lower (0·76–0·80). In contrast, the ICC for BMI was only 0·52 (not shown), indicating the need to adjust BMI for age. Among the 935 children whose initial BMI was at or above the 85th percentile, the ICCs for the adjusted metrics (0·70–0·71) were larger than those for BMIz (0·62) and the unadjusted metrics (0·54–0·60), with the lowest ICC seen for distance from the median. The ICCs of the adjusted metrics were also substantially higher than those for BMIz and the unadjusted metrics in the subsets of children with higher values of their initial BMI (above the 95th or 97th percentiles). Among the seventy-four children who had an initial BMI ≥ 120 % of the 95th percentile, the ICC for adjusted log % distance from the median was lower (0·42) than were the ICCs for the other adjusted metrics (0·50).
Table 3. Comparison of unadjusted and adjusted intraclass correlation coefficients at initial examination

BMIz, BMI-for-age z score; M, median; S, generalised CV.
* Adjusted using the reference values of M and S at age 20 years.
Fig. 2 shows that the ICCs rose with age at first examination, with the adjusted metrics performing better than the unadjusted, particularly in the youngest children. Beyond age 9 years, the unadjusted and adjusted metrics, particularly for % distance, performed similarly. Of the unadjusted metrics, absolute distance from the median performed worst, while the three adjusted metrics performed similarly at all ages.

Fig. 2. Intraclass correlation coefficients for unadjusted (![]() ) and age-adjusted (
) and age-adjusted (![]() ) distance from the median (a), % from median (b) and log % from median (c) by age at first examination. The points represent the mean age at first examination in each group.
) distance from the median (a), % from median (b) and log % from median (c) by age at first examination. The points represent the mean age at first examination in each group.
Fig. 3 shows the ICCs falling with increasing time interval between the first and last examination, indicating lower tracking as the length of follow-up increased. For intervals <3 years (mean 2·5 years), little difference in the ICCs of the six metrics was observed. For longer intervals, the ICCs fell more steeply for the unadjusted metrics, particularly distance from the median, while the ICCs for the adjusted metrics were similar.

Fig. 3. Intraclass correlation coefficients for unadjusted (![]() ) and age-adjusted (
) and age-adjusted (![]() ) distance from the median (a), % from median (b) and log % from median (c) by the interval between the first and last examinations. The points represent the mean interval in each group.
) distance from the median (a), % from median (b) and log % from median (c) by the interval between the first and last examinations. The points represent the mean interval in each group.
Analyses of the ICCs stratified both by time interval and age at first examination (not shown) confirmed little difference in the ICCs of the six metrics at any age among children re-examined within 3 years. Over longer time intervals, the ICCs of the adjusted metrics were larger than those of the unadjusted metrics for children first examined before 9 years of age.
Discussion
Despite the limitations of BMIz score based on the LMS parameters of the CDC growth charts for children with severe obesity(Reference Freedman, Butte and Taveras10, Reference Woo11, Reference Flegal, Wei and Ogden14, Reference Berkey and Colditz15, Reference Kelly and Daniels33), it continues to be widely used for children with very high BMI(Reference Wang, Cai and Wu34–Reference O’Connor, Evans and Burda38). As an alternative, we explored metrics that express a child’s BMI as the absolute or percentage distance from their median BMI for age and sex. These metrics use the M and S parameters of the CDC growth charts and can be adjusted for age.
A desirable property of a BMI metric is that it should track over time, so that changes can be identified. We assessed this tracking using the ICC, a statistic that contrasts between-child and within-child variability. Because these alternative metrics, unlike BMIz, do not compress very high BMIs into a narrow range that varies by sex and age, it is likely that they will more accurately characterise the BMIs of children in both epidemiologic and clinical research. These metrics may be particularly useful when assessing the BMI and longitudinal changes in BMI of children with a BMI ≥ 97th percentile.
We found that when adjusted for age, the three BMI metrics performed similarly to BMIz among all children, unsurprisingly given that they are derived from the LMS transformation. However, among children who were (1) overweight or had obesity, (2) younger and (3) followed for >3 years, the ICCs of the adjusted metrics were appreciably higher than those of the unadjusted metrics. Of note, the effects of initial age and length of follow-up were largely independent. Of the unadjusted metrics, the ICCs for % distance from median and log % distance from median were larger than those for distance from median, particularly at younger ages and over longer time intervals. There was little difference between the age-adjusted linear and log forms of % from the median in most analyses, among the seventy-four children who had an initial BMI ≥ 120 % of the 95th percentile, the ICC for the linear % distance was larger than for the log % distance (0·50 v. 0·42).
These results are related to the parameters underlying the CDC growth charts. The M and S values of these parameters in these charts are very different before and after age 12 years(Reference Freedman, Butte and Taveras10, 27), with M rising almost linearly after age 6 years and S increasing steeply between age 5 and 12 years and then stabilizing. The higher ICCs for unadjusted % distance compared with absolute distance reflect the CV S being less age dependent than the sdM × S.
The lower ICCs for BMIz among children with a high BMI reflects its compression at the upper end(Reference Flegal and Cole3, Reference Freedman, Butte and Taveras9, Reference Woo11, Reference Flegal, Wei and Ogden14, Reference Cole, Faith and Pietrobelli16). Further, the effect of age adjustment is larger among overweight and obese children because (a) the metrics reflect distance from the median, (b) this distance is greater for children with a high BMI and (c) the effect of age adjustment is to scale the distance by M and/or S, both of which are greater at age 20 years compared with younger ages. It could be argued that a BMI metric should be selected based on the magnitude of its association with risk factors(Reference Dwyer and Blizzard39, Reference Williams, Going and Lohman40), but this may be difficult because cross-sectional correlations with risk factor levels are low (r approximately 0·2–0·4)(Reference Freedman, Katzmarzyk and Dietz41, Reference Steinberger, Jacobs and Raatz42) and the variability of these characteristics is strongly age dependent.
The BMI metrics assessed in the present study could be used in conjunction with the current cut points for overweight (85th to 94th percentiles) and obesity (BMI ≥ 95th percentile) in the CDC growth charts. Although the adjusted BMI metrics correspond more closely to the BMI centiles in the growth charts compared with the unadjusted metrics, it should be realised that there are substantial differences by sex and age. For example, the mean (range) adjusted % distance corresponding to the 95th centile is +33 % (26–37) among boys and +40 % (29–46) among girls. Levels of the adjusted metrics also differ substantially by race/ethnicity.
A reviewer suggests that accounting for kurtosis in the BMI distribution might alleviate the skewness problem and the resulting compression of very high BMIs into a narrow z score range. For example, the WHO child growth standards explored modelling kurtosis in the BMI distribution by fitting the Box–Cox power exponential distribution(43). However, attempts to model the BMI distribution in the CDC growth charts using the Box–Cox power exponential or Box–Cox t distribution(Reference Rigby and Stasinopoulos44) resulted in many values of the L (skewness) parameter being more negative compared with the current CDC growth charts. Therefore, adjusting for kurtosis does not alleviate the problem of extreme skewness in the CDC growth charts.
Several limitations of our results should be considered. Because the prevalence of obesity (BMI ≥ 95th percentile) is much lower in these analyses (9 %) compared with the current status in the USA (18·5 %)(Reference Hales, Fryar and Carroll45), it is possible that we underestimated the importance of age adjustment among contemporary children. Further, methods other than the ICC could be used to evaluate tracking, such as examining the ability of a high BMI to predict a high BMI in later life. It should also be noted that though we did not assess the other alternative BMI metrics that have been proposed, that is, modified z score(Reference Chambers, Tanamas and Clark18, 19) and %BMIp95(Reference Freedman, Butte and Taveras10, Reference Flegal, Wei and Ogden14, Reference Gulati, Kaplan and Daniels17, Reference Kelly, Barlow and Rao46), these two metrics were highly correlated (r > 0·95) with adjusted % distance from the median. However, values of % distance from the median are more closely tied to the CDC growth charts and may be more interpretable than modified BMIz or %BMIp95. As levels of these alternative BMI metrics likely vary by race/ethnicity, it would also be possible to examine these metrics within various subgroups.
Conclusions
Although BMIz continues to be widely used among children with very high BMI, it has serious limitations when BMI exceeds the 97th percentile. Of the alternatives we examined, % distance from median is better than absolute distance from median based on their ICCs. Although log % distance from median partially accounts for the skewness of the BMI distribution, we found some evidence to suggest that adjusted % distance from the median on the linear scale may be superior. These alternative BMI metrics could supplement the current cut points in the CDC growth charts and would provide a more nuanced assessment for BMI over the 99th percentile to a wider audience (including families of children who have a very high BMI). These alternative metrics would also be useful in the long-term studies that assess the effects of obesity interventions among children with very high BMIs. For clinical purposes, it would also be possible to generate charts illustrating these metrics for children with BMI over the 97th percentile.
Acknowledgements
We acknowledge the importance of Dr Gerald Berenson, who died on 22 November 2018, in this analysis. Dr Berenson contributed to the earlier development and writing of this manuscript and provided key observations. Dr Berenson started the Bogalusa Heart Study in 1972 and was the director for more than 30 years. The findings of the Bogalusa Heart Study showed that that the major aetiologies of atherosclerosis, CHD and hypertension begin in childhood. This has resulted in worldwide preventive programmes to encourage exercise and better nutrition among children.
This work was supported by the National Institutes of Health (J. H. X.: National Institute on Aging Grant AG-16592; National Heart, Lung, and Blood Institute Grants HL-38844 and HL-121230).
D. S. F. conceptualised and performed the analysis, drafted the initial manuscript, and revised the manuscript. T. J. C. and J. G. W. extensively critically reviewed and revised the manuscript. C. L. O. and J. H. X. reviewed the manuscript for important intellectual comment. All authors approved the final manuscript as submitted and agree to be accountable for all aspects of the work.
The authors declare no conflicts of interest. The findings and conclusions in this report are those of the authors and do not represent the official position of the CDC.









