Voluntary food intake (FI) of animals can be predicted only on the basis of a sufficient description of the food(s), the animal and its environment (Emmans & Kyriazakis, Reference Emmans and Kyriazakis2001; Yearsley et al. Reference Yearsley, Tolkamp and Illius2001). When extremes in the physical environment are avoided and animals are housed individually, under fixed day length and in the absence of disease, models of FI must include at least some animal and food characteristics to give good predictions (e.g. Agricultural Research Council (ARC), 1980; National Research Council, 1987). There is extensive literature on the effects of food quality on the FI of sheep, even though the most appropriate framework for such predictive intake models for ruminants is still contentious (e.g. Ketelaars & Tolkamp, Reference Ketelaars and Tolkamp1992, Reference Ketelaars and Tolkamp1996; Emmans & Kyriazakis, Reference Emmans and Kyriazakis1995; National Research Council, 2001; Pittroff & Kothmann, Reference Pittroff and Kothmann2001; Illius et al. Reference Illius, Tolkamp and Yearsley2002). Much less work has been done on the effects of variation in animal state (especially fatness) on FI and fatness is rarely included in intake models for sheep (see Pittroff & Kothmann, Reference Pittroff and Kothmann2001 for a review). It is, however, evident that the fatness of a sheep has a considerable effect on its FI (see Tolkamp et al. Reference Tolkamp, Emmans and Kyriazakis2006, for a recent analysis).
Tolkamp & Ketelaars (Reference Tolkamp and Ketelaars1992) proposed that the effect of food quality on FI is mediated by the efficiency with which sheep can utilise the metabolisable energy (ME) that is consumed. Several tests of their model showed good correspondence between predicted and observed FI (Tolkamp & Ketelaars, Reference Tolkamp and Ketelaars1992; Ketelaars & Tolkamp, Reference Ketelaars and Tolkamp1996). They speculated that the effect of body fatness on FI could act via the same mechanism, if fat animals utilise the ME of a given food with a lower efficiency. At the time they found very little evidence for that (Tolkamp & Ketelaars, Reference Tolkamp and Ketelaars1992). This failure to account for the effects of animal fatness on FI was one of the major criticisms of Emmans & Kyriazakis (Reference Emmans and Kyriazakis1995) on that intake model. However, empirical data have been found since that show that body fatness affects the efficiency with which sheep utilise energy of a given food (Ketelaars & Tolkamp, Reference Ketelaars and Tolkamp1996).
In addition, a likely mechanism for such an effect of fatness on energetic efficiency has now been identified. Adipose tissue produces signals (particularly in the form of the hormone leptin) that have a profound effect on a variety of metabolic and physiological processes, and on animal behaviour (e.g. Houseknecht et al. Reference Houseknecht, Baile, Matteri and Spurlock1998; Schneider et al. 1998; Macajova et al. Reference Macajova, Lamosova and Zeman2004). An increase in body lipid content results in an increase in plasma leptin concentration (Delavaud et al. Reference Delavaud, Bocquier, Chilliard, Keisler, Gertler and Kann2000). Such an increase is associated with both an increase in energy expenditure (Wang et al. Reference Wang, Hartzell, Rose, Flatt, Hulsey, Menon, Makula and Baile1999) and a decrease in FI (e.g. Friedman & Halaas, Reference Friedman and Halaas1998). This seems very relevant in the context of the present paper because, if leptin affects energetic efficiency, then the model of Tolkamp & Ketelaars (Reference Tolkamp and Ketelaars1992) can be adapted to include effects of animal fatness on FI.
It is, therefore, the first objective of this paper to construct a predictive FI model based on the assumption that body fatness affects the efficiency with which ME is utilised. The model is parameterised and subjected to a first test using data collected with lambs. The second objective is to expand this FI model to predict lamb performance (in terms of changes in body weight and lipid content), using a simulation model, and to test the predictions against data obtained with sheep. Finally, the model is used to predict how food quality and body fatness interact to determine the final body weight and lipid content of animals that have long-term access to a single food.
Material and methods
The rules used in the intake model
Effects of food quality on energetic efficiency in sheep
To describe effects of food quality on the efficiency of energy utilisation in ruminants, a standard equation has been adopted in the UK (see ARC, 1980; Agricultural & Food Research Council, 1993). It is a ‘diminishing rate of return’ model in the shape of a Mitscherlich equation:
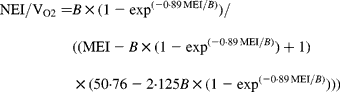
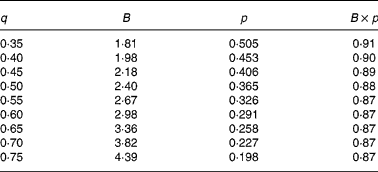
In agreement with the ARC (1980), in Equation 1 the metabolisable energy intake (MEI) and net energy intake (NEI) are scaled with the net energy for maintenance (NEm), all measured in MJ/d, to make the model applicable across animals with different NEm. B and p are model parameters that can be estimated directly with Equation 1 from data sets of measured MEI, NEI and NEm or indirectly from the efficiency of ME utilisation for maintenance and gain (see ARC, 1980). Parameter B represents the asymptote of the equation and p is a rate parameter that determines how quickly NEI approaches B as MEI increases. Food quality affects both the B and the p parameters. Table 1 gives the ARC's (1980) preferred values for B and p for foods of different metabolisability (q, i.e. the ratio of the ME and gross energy contents of a food). Table 1 shows that, as q increases, the values for B and p systematically increase and decrease, respectively.
Table 1 Agricultural Research Council's (1980) preferred estimates for parameters B and p in the model NEI=B×(1−exp(−p×MEI)) in relation to food metabolisability q (the ratio of the food's metabolisable energy to gross energy content)
The relationship between parameters B and p
Figure 1 shows a plot of p against B values for sixty-five foods as estimated in 551 respiration trials with 222 cattle and sheep (from Blaxter & Boyne, Reference Blaxter, Boyne, Schurch and Wenk1970). The plot shows that there is an almost inverse relationship between parameters B and p and that for a given B value, there is little variation in p value. Table 1 shows that the products of the preferred values for B and p as given by the ARC (1980) vary little around their mean value of 0·88. This mean is similar to the mean value (0·89) of the product of B and p for the large data set depicted in Fig. 1. These data show, therefore, that there is almost no effect of food quality on the product of B and p. Table 1 and Fig. 1 show that the assumption B × p = 0·89 gives a good description of the data. We have used this relationship for the development of our model and discuss its implications later.

Fig. 1 The relationship between the parameters p and B in the model NEI = B × (1 − exp( − p × MEI)) for sixty-five different foods (●, as read from Fig. 2 in Blaxter & Boyne, Reference Blaxter, Boyne, Schurch and Wenk1970) and according to the Agricultural Research Council's (1980, p. 104) preferred values (![]() , as in Table 1). Also shown are the curves p = 1/B (- - -) and p = 0·89/B (—).
, as in Table 1). Also shown are the curves p = 1/B (- - -) and p = 0·89/B (—).
The effects of energetic efficiency on intake of different foods in mature sheep
Tolkamp & Ketelaars (Reference Tolkamp and Ketelaars1992) have shown that the voluntary FI of sheep that are offered different food qualities can be quite accurately predicted by an optimisation model that is based on assumed benefits and costs. In this model, the benefits of feeding are directly proportional to NEI and the costs are directly proportional to oxidative metabolism (Tolkamp & Ketelaars, Reference Tolkamp and Ketelaars1992). These costs can be derived directly from Equation 1. Heat production (HP) scaled with NEm is by definition equal to MEI − NEI+1. To estimate oxygen consumption (VO2, expressed in l/d) from HP, effects of intake level relative to maintenance on RQ have to be taken into account. We used the equation:
based on Blaxter's (Reference Blaxter1989) calculations, for that purpose. For each food quality, the NEI and, consequently, the MEI at which the ratio NEI/VO2 reaches its maximum value can then be calculated (see later). This is the predicted ad libitum intake for this food (see Tolkamp & Ketelaars, Reference Tolkamp and Ketelaars1992; Ketelaars & Tolkamp, Reference Ketelaars and Tolkamp1996, for extensive discussions of the model).
Modelling the effects of animal state (fatness) on food intake
The equality B × p = 0·89 reduces Equation 1 to an equation with only one parameter since p can be replaced with 0·89/B:
The benefit/cost ratio is then given by Equation 4:
As before, NEI, VO2 and MEI in Equations 2–4 are all expressed relative to NEm. For a given B value, the MEI at which the NEI/VO2 ratio reaches its maximum value can be calculated from Equation 4. Similarly, for any observed MEI, the B value can be estimated for which this intake occurs at the maximum NEI/VO2 ratio. How animal state affects energetic efficiency as measured by B can then be estimated from a suitable data set that provides sufficient information to estimate NEm, MEI and animal fatness. Such a data set was collected with lambs and the main features of that experiment are summarised later. A number of additional assumptions had to be made before these data could be used to simulate changes in weight and body composition and these are discussed subsequently.
Experimental data used to derive parameters and test model predictions
Experimental design
The data used were from a 50-week experiment with individually penned Texel × Greyface ewe lambs with a mean initial full body weight (FBW) of 35·3 (se 0·3) kg (Tolkamp et al. Reference Tolkamp, Emmans and Kyriazakis2006). For the present analysis we used lambs from five experimental groups (see Table 2) and all animals had access ad libitum to one of two foods at a time: chopped grass hay (H) or a pelleted concentrate diet (P). Group H received H throughout the entire experiment. Groups P45H and P65H received P until their FBW was around 45 or 65 kg, respectively, and group P95H received P until experimental week 40 (when their FBW was around 95 kg). After that, lambs were switched to H until the end of the experiment. Lambs in group H45P received H until they reached 45 kg FBW and they were then switched to P.
Table 2 Experimental design, indicating number of lambs per treatment group and period*
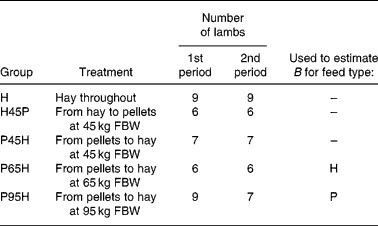
* Lambs in treatment group H received one food (chopped hay, H) throughout the entire 50-week experimental period. The other treatment groups received one food, H or pelleted concentrates (P), during the first period but when they reached a certain full body weight (FBW) they were switched and received the other food during the second period of the experiment. Indicated are also the two treatments that were used to derive estimates of parameter B in the model NEI = B × (1 − exp( − 0·89 MEI/B)) for foods H and P, respectively.
The ME contents of H and P were estimated at 7·9 and 8·5 MJ/kg fresh food, respectively (see Tolkamp et al. Reference Tolkamp, Emmans and Kyriazakis2006 for details). The crude protein content was analysed as 91 and 176 g/kg DM, and the metabolisable protein (MP) yield of the foods was estimated (Agricultural & Food Research Council, 1993) to be 48 and 90 g/kg of fresh H and P, respectively. Figure 2 shows the FBW, condition score (CS) and FI relative to body weight of the different treatments during the experiment.

Fig. 2 Experimental data used to parameterise Equation 3 and to test predictions from the intake and simulation models. Group-mean observed full body weight (FBW; a) and condition score (b) against experimental week for all treatment groups. Hay (c) and pellet (d) intake relative to FBW. Groups received either pellets up to 95 kg FBW and subsequently hay (P95H, ●), pellets up to 65 kg FBW and subsequently hay (P65H, ![]() ), pellets up to 45 kg FBW and subsequently hay (P45H, ▾), hay throughout (H, ○) or hay up to 45 kg FBW and subsequently pellets (H45P, +).
), pellets up to 45 kg FBW and subsequently hay (P45H, ▾), hay throughout (H, ○) or hay up to 45 kg FBW and subsequently pellets (H45P, +).
Additional rules used in the model to predict intake
Empty body weight (EBW) was derived from FBW using the ARC (1980) formula FBW = 1·09 × (EBW+a) with a = 5 for hay and a = 2 for pellets. Fleece-free empty body weight (ffEBW) was calculated assuming wool weight to be 5·9 % of FBW throughout the experiment (Tolkamp et al. Reference Tolkamp, Emmans and Kyriazakis2006).
CS was assessed every second week on a scale of 0 (severely emaciated) to 5 (extremely fat) with quarter-point intervals (Russel et al. Reference Russel, Doney and Gunn1969). Individual data were smoothed and interpolated to provide weekly estimates of CS (Tolkamp et al. Reference Tolkamp, Emmans and Kyriazakis2006). The data obtained with ewes by Russel et al. (Reference Russel, Doney and Gunn1969) were used to establish the appropriate relationship between CS and the lipid proportion in the ffEBW (Lip) and vice versa. Russel et al. (Reference Russel, Doney and Gunn1969) found the linear relationship: Lip = 0·0269+0·0869 × CS (residual standard deviation (RSD) = 0·0254; mean CS = 2·13; mean Lip = 0·212). However, the intercept in this relationship was not significantly different from zero and a regression line without intercept gave the equation Lip = 0·1 × CS. This relationship and its inverse CS = 10 × Lip were used in all models. Lean weight was calculated as ffEBW minus lipid weight.
The NEm (MJ/d) and MP (g/d) requirements were calculated for each individual as being directly proportional to lean weight. According to the inter-species relationship developed by Emmans (Reference Emmans1997), animals with a mature protein mass of 11 kg (see later) have a NEm of 220 kJ/kg actual lean weight. Since sheep have a lower NEm than the interspecies mean (by about 10 %; ARC, 1980; Blaxter, Reference Blaxter1989), we decreased this estimate to 200 kJ/kg lean weight. MP requirements for maintenance (g/d) were converted from the Agricultural & Food Research Council (1993) estimates as being proportional to lean weight (1·2 g/kg lean weight).
Estimating effects of animal fatness on parameter B
For an animal with a known FBW, CS and FI, and a food with a known ME content, the rules set out earlier allow the calculation of the MEI/NEm ratio. We assumed that the observed voluntary MEI was the result of an optimisation process that maximises NEI/VO2 as described earlier and estimated the appropriate B value. As such B values cannot be derived algebraically from Equation 4 for a given MEI/NEm ratio, a FORTRAN program was used to find the B value that would predict exactly the observed voluntary intake. This procedure was repeated for the weekly data of individual animals in two of the experimental treatments described earlier. To estimate the effects of fatness on B values for H, data from animals in treatment group P65H (last period) were used. To estimate effects of fatness on B values for P, data from animals in treatment group P95H (first period) were used. These groups were selected because they showed most variation in CS (see Fig. 2(b)) and were, therefore, most suitable to estimate effects of body fatness on B. Subsequently, the weekly group-means of individual B values were plotted against the weekly group-mean lipid to lean ratios (lipid/lean) to investigate the nature of this relationship. Linear regression analysis was used to estimate effects of lipid/lean on B values.
Intake predictions using observed full body weight and condition score values
The relationships between the lipid/lean ratio in the ffEBW and the B values for foods H and P derived as described earlier were subsequently used to predict voluntary intake of the other three treatment groups (H, H45P and P45H) consisting of lambs with very different nutritional histories. First, the lipid/lean ratios were calculated for all individuals in these groups for all experimental weeks using the rules provided earlier and the corresponding B values were derived from the regression equations derived from observations obtained with animals in treatments P95H and P65H. Subsequently, Equation 4 was used to predict individual weekly intakes and the group-means of the weekly predictions were compared with the observed group-means.
Additional rules used in the simulation models
The NE contents of lipid and of protein that was deposited (or mobilised) were taken as 39·6 and 23·6 MJ/kg, respectively (Emmans, Reference Emmans1994). MP was assumed to be utilised for maintenance and gain with efficiencies of 100 and 59 %, respectively (Agricultural & Food Research Council, 1993). Lean weight gain was estimated, after correcting for protein retention in wool, as 4 × protein gain. Protein retention in wool (g/d) was estimated according to the Agricultural & Food Research Council (1993) as (3+0·1 × protein retention in ffEBW).
We relied on a Gompertz function to describe maximum protein gain. This function has been successful in describing body weight gain as well as potential protein gain in a variety of species (Emmans, Reference Emmans1997). The maximum daily protein gain of an animal that grows protein according to a Gompertz curve can be expressed (Lewis et al. Reference Lewis, Emmans, Dingwall and Simm2002) as dP/dt = C × P × ln(A/P) in which dP/dt = maximum daily protein retention; A = mature protein mass; P = actual protein mass; C = growth parameter. Parameter A was estimated at 11 kg (Emmans, Reference Emmans1997; Jones et al. Reference Jones, Amer, Lewis and Emmans2004) and C was estimated as 0·23/A 0 ·27 (Emmans, Reference Emmans1997), multiplied by a correction factor (0·67) as has been used before in sheep (Jones et al. Reference Jones, Amer, Lewis and Emmans2004). To simulate FI and animal performance for lambs in each of the treatments, our starting position was a lamb of around 35 kg with lean and lipid body masses of 19·5 and 7 kg, respectively (corresponding to a CS of 2·6). These were used to estimate the NEm, the lipid/lean ratio and, consequently, the most appropriate B value. These estimates were used to predict MEI, NEI and MP intake for day 1. It was assumed that lambs would utilise all available MP above maintenance requirements for protein retention as long as the maximum, according to the Gompertz curve, was not exceeded. If the amount of available MP for deposition exceeded that amount, the animal was assumed to grow lean according to the Gompertz curve. The amount of NE associated with protein gain was calculated and, together with NEm, subtracted from the NEI. If this resulted in a positive value, this was assumed to be lipid retained. If the resulting value was negative it was assumed that the lamb mobilised energy from lipid. To take account of the variable intake at a given FBW, gut fill was estimated as six times hay intake and 2·5 times pellet intake (derived from ARC, 1980). Using the rules given earlier, the resulting changes in lean and lipid weight, FBW and CS were calculated for day 1 and the ‘updated’ animal served as input for day 2 of the simulation, etc. One simulation was carried out for a lamb consuming hay for 50 weeks (to simulate treatment group H). In the other simulations, lambs received one food until animals entered week 41 (group P95H) or their simulated FBW reached the treatment mean FBW at which animals were switched to another food. Subsequently, the simulation was continued using the appropriate values for the other food to simulate each of our treatment groups (as in Fig. 2). For our extrapolation of the model to estimate final FBW and lipid content of lambs fed H or P continuously, this process was repeated for 1500 d for both foods.
Results
Relationship between lipid/lean and estimated B values in groups P95H and P65H
Figure 3(a) shows the group-mean estimates of B against the group-mean lipid/lean ratios up to experimental week 40 for group P95H (i.e. the period animals consumed pellets) and during the last 35 experimental weeks for group P65H (i.e. the period animals consumed hay). In both cases lower B values were associated with higher lipid/lean ratios. Linear regression analysis showed an obvious effect of food type on the intercept (P < 0·0001) but no food type effect on the slope (P = 0·96). Figure 3(a) shows the regression lines with a common regression coefficient ( − 4·151) and intercepts of 7·26 and 3·18 for foods P and H, respectively (RSD = 0·23, R 2 0·98).

Fig. 3 The relationship between the estimate for B and the lipid/lean ratio in the empty body. (a), Data and the regression lines that were used for intake predictions based on means, calculated per week, for sheep consuming pellets from treatment P95H (●) and sheep consuming hay from treatment P65H (▲); also depicted is the mean of all animals with condition score of 5, i.e. at a lipid/lean ratio of 1. The regression lines have both a slope of − 4·151 and intercepts of 7·26 and 3·18, respectively (R 2 0·98, RSD = 0·23). (b), The estimates for groups H45P (○), H and P45H (Δ) and P95H (![]() ) are added to the observations of (a); the regression lines are those in (a) with the constant value of 0·82 added for food H at high lipid/lean ratios. For an explanation of treatment codes, see Fig. 2.
) are added to the observations of (a); the regression lines are those in (a) with the constant value of 0·82 added for food H at high lipid/lean ratios. For an explanation of treatment codes, see Fig. 2.
Equation 3 predicts that MEI will supply enough NE for maintenance (NEm) only when the B value is 1·68. All estimated B values for food P were higher than this. Extrapolation of the regression line predicts that such a B value for P will be achieved in animals with a lipid/lean ratio of 1·38, which corresponds with a lipid proportion in the ffEBW of 1·38/2·38 = 0·58. Estimated B values for the hay were mostly lower than 1·68, suggesting that group P65H lambs generally were in negative energy balance during the period they received hay.
Predicted food intakes for groups H45P, H and P45H
The B values for H that were derived according to the method described earlier were used to predict intake of individual animals in treatment group H and in treatment group P45H while lambs consumed H. Similarly, the regression line derived with data obtained for food P and shown in Fig. 3(a) was used to predict intake for animals in treatment H45P while they consumed P. The group-mean predictions and observations are shown in Fig. 4. For all treatment groups, the predicted trend in intake change matches the observations closely. On average, predicted intakes were higher than observed in group H (by 1·1 (se 0·9) %) but lower than observed intakes in groups P45H (by − 0·5 (se 1·0) %) and H45P (by − 5·1 (se 1·5) %).

Fig. 4 Observed (○) and predicted (●) fresh food intake for (a) group H, (b) group P45H, all compared at the same experimental week and for (c) group H45P, against synchronised weeks since the change from hay to pellets. For an explanation of treatment codes, see Fig. 2.
We intended to use the regression line of B on the lipid/lean ratio to also predict the hay intake during the last 10 weeks of group P95H. It was evident, however, that linear extrapolation of this line would predict negative values for B and then Equation 4 cannot be interpreted. To derive the shape of the relationship between B and animal fatness for very fat sheep, we estimated for group P95H (as well as for the other groups, see Fig. 3(b)) the B values from their intake levels and related these to the estimated lipid/lean ratios. For most groups, the estimated B values agreed rather well with those estimated for groups P65H (for hay) and P95H (for pellets). However, Fig. 3(b) shows that for animals in group P95H consuming hay the estimated B values did not vary systematically with the lipid/lean ratio and averaged 0·82. This value was similar to the B values observed for the animals in group P65H while these were fat.
Simulated intake and performance of lambs in all treatment groups
Figure 5 shows the results of the predictions of the simulation model together with the group-means observed. The simulation of the FBW of lambs receiving P (i.e. the first part of treatments P45H, P65H and P95H and the last part of treatment H45P) was very close to the group-means observed. Also the simulated CS for lambs receiving P followed the observations very accurately for treatment H45P and the average of treatments P45H, P65H and P95H during the first part of the experiment. Lambs in treatment P95H had the lowest CS of animals receiving pellets during the first part of the experiment and the observed values for lambs in this treatment were slightly lower than simulated during the first 40 weeks of the experiment. The simulated CS of lambs receiving H were also close to observations for all treatment groups (see Fig. 5(b)) except P95H where simulated values are again slightly higher than observations during the last 10 weeks of the experiment. Simulated FBW of lambs that received H were not always as accurate as they were for lambs receiving P. The observations and simulated FBW were similar for treatments H, P45H and P95H. However, the simulated FBW of lambs receiving H in treatment P65H were predicted to first decrease and then increase again. In contrast, the observed group-mean FBW was almost constant during the last 30 weeks of the experiment.

Fig. 5 The fit of the full body weight (a) and condition score (b) predicted by the simulation model (see Materials and Methods) as indicated by the solid lines to the group-mean observations for treatments P95H (●), P65H (![]() ), P45H (▾), H (○) and H45P (+). For an explanation of treatment codes, see Fig. 2.
), P45H (▾), H (○) and H45P (+). For an explanation of treatment codes, see Fig. 2.
Predicted final body weights and lipid contents of lambs fed hay or pellets only
Figure 6 shows the extrapolation to 150 weeks of the simulation model for a lamb with an initial FBW of 35 kg and a CS of 2·6 that continuously consumes either H or P. The simulation model predicted that FBW would stabilise at 77 and 118 kg for animals receiving H or P and that the associated lipid contents in the EBW would then be 26 and 58 %, respectively.

Fig. 6 Extrapolations of the simulation model that predict the full body weights (a) and lipid contents (b) in the empty body of ewes that consume hay (lower curves) or pellets (higher curves) throughout.
Discussion
Underlying rules and assumptions
Intake in relation to energetic efficiency
The intake model developed by Tolkamp & Ketelaars (Reference Tolkamp and Ketelaars1992) is based on the assumption that an increase in FI not only provides the animal with increased benefits (notably available energy) but is also associated with increased costs. The idea that animals may optimise their (feeding) behaviour in relation to both benefits and costs is not uncommon, especially in the behavioural ecology literature (e.g. Stephens & Krebs, Reference Stephens and Krebs1986; Houston & McNamara, Reference Houston and McNamara1999). The model of Tolkamp & Ketelaars (Reference Tolkamp and Ketelaars1992) defined benefits in terms of intake of net energy, a widely used currency (e.g. Stephens & Krebs, Reference Stephens and Krebs1986), and costs in terms of oxidative metabolism. Damage caused by oxidative metabolism is a major factor in the occurrence of many diseases and the gradual loss of vitality and of ageing (for reviews see e.g. Finkel & Holbrook, Reference Finkel and Holbrook2000; Ramsey et al. Reference Ramsey, Harper and Weindruch2000; Hunt et al. Reference Hunt, Hyun, Allard, Minor, Mattson, Ingram and de Cabo2006; Terman & Brunk, Reference Terman and Brunk2006). For instance, a decrease in energy expenditure leads to a much lower frequency of lesions and tumours long before animals die (Berg & Simms, Reference Berg and Simms1960) and protection against oxidative damage leads to more active animals long before senescence occurs (Orr & Sohal, Reference Orr and Sohal1994). In addition, increased energy expenditure can have negative effects on the functioning of the immune system (e.g. Houston & McNamara, Reference Houston and McNamara1999) and on reproductive performance (Johnston et al. Reference Johnston, Grune and Bell2006). Oxidative damage, therefore, has clearly fitness consequences and, for that reason, costs of feeding in the present paper were assumed to vary depending on oxidative metabolism which is affected directly by energetic efficiency. The ratio NEI/VO2 was preferred over the ratio NEI/energy expenditure (as discussed by Stephens & Krebs, Reference Stephens and Krebs1986) because the requirements for such an assumption are unlikely to be met (see discussion by Tolkamp et al. Reference Tolkamp, Emmans, Yearsley and Kyriazakis2002).
It is well established that ruminants utilise the ME of foods with varying efficiency (ARC, 1980). Similar intakes of NE from foods of different quality are associated with widely different costs in term of oxidative metabolism and this is the basis of Equation 4. Tolkamp & Ketelaars (Reference Tolkamp and Ketelaars1992) hypothesised that the parameters in Equation 4 would change gradually as animals matured and became fatter. This was supported by Ketelaars & Tolkamp (Reference Ketelaars and Tolkamp1996) who re-analysed data collected in respiration experiments by Graham (Reference Graham1969) with sheep that differed in maturity. When Equation 1 was fitted to these data the results showed that estimated B values decreased and p values increased with level of fatness. As a result, the predicted optimum NEI/NEm changed in the direction of 1 when animals matured. This was the first empirical evidence that animal state can indeed affect efficiency of ME utilisation in sheep.
Since that time, new information about the mechanisms linking animal fatness and animal metabolism has become available. It is now evident that lipid tissue is not metabolically inert, as once thought, but produces adipocytokines including leptin, which can have a large effect on the physiology and behaviour of animals (e.g. Maffei et al. Reference Maffei, Halaas and Ravussin1995; Lord et al. Reference Lord, Matarese, Howard, Baker, Bloom and Lechler1998; Ehrhardt et al. Reference Ehrhardt, Slepetis, Siegal-Willott, Van Amburgh, Bell and Boisclair2000; Schneider et al. Reference Schneider, Zhou and Blum2000; Macajova et al. Reference Macajova, Lamosova and Zeman2004; Meier & Gressner, Reference Meier and Gressner2004; La Cava & Matarese, Reference La Cava and Matarese2004; Ahima, Reference Ahima2005), including sheep (Delavaud et al. Reference Delavaud, Bocquier, Chilliard, Keisler, Gertler and Kann2000; Blache et al. Reference Blache, Tellam, Chagas, Blackberry, Vercoe and Martin2000; Daniel et al. Reference Daniel, Whitlock, Baker, Steele, Morrison, Keisler and Sartin2002). Higher blood leptin levels result in a change in energy partitioning towards oxidative metabolism (Friedman & Halaas, Reference Friedman and Halaas1998; Houseknecht et al. Reference Houseknecht, Baile, Matteri and Spurlock1998), as is demonstrated most convincingly by pair-feeding (Wang et al. Reference Wang, Hartzell, Rose, Flatt, Hulsey, Menon, Makula and Baile1999). If an increase in body fatness increases blood leptin levels and, consequently, energy expenditure, the result will be a decrease in energetic efficiency. This suggests a possible mechanism to explain the observation that the efficiency with which sheep utilise ME from a given food depends on the fatness of the sheep that consumes it. Then the effects of body fatness on FI of sheep can be readily incorporated into a model that uses variation in energetic efficiency to predict FI. We, therefore, set out to investigate how effects of fatness on FI could best be incorporated into the existing model based on Equation 1. To that end, we had to determine first how sheep fatness would affect the parameters in this equation.
The relationship between B and p
The relationship between NEI and MEI in Equation 1 is determined by the values of parameters B and p. Blaxter & Boyne (Reference Blaxter, Boyne, Schurch and Wenk1970) noticed that, across foods, variation in B is not independent of variation in p. In particular, they investigated the possibility that B could be equal to the inverse of p but concluded that this resulted in a model that gave a worse fit to the data. Blaxter & Boyne (Reference Blaxter, Boyne, Schurch and Wenk1970) may have been unaware of the physiological significance of the hypothesis that B × p would be unity. This significance is best demonstrated by analysis of the first derivative of Equation 1 with respect to MEI:
This first derivative, that is the partial efficiency of ME utilisation, approaches B × p when MEI approaches zero. Therefore, B × p is the first derivative of Equation 1 in the origin and represents the efficiency with which the first J of MEI is utilised. The hypothesis that B × p would be equal to unity can therefore only be physiologically meaningful if two assumptions are valid, i.e. (1) that there is no effect of food quality on the partial efficiency of ME utilisation for the first J of ME that is consumed and (2) that this efficiency is 100 %. Although there may be no a priori reason to believe that the first assumption should be false, the second one seems highly unlikely. The stoichiometry of the reactions producing ATP from various substrates suggest that animals will utilise energy in the form of fermentation end-products with a lower efficiency than energy from body lipid reserves (Alberts et al. Reference Alberts, Bray, Lewis, Raff, Roberts and Watson1989), which has been confirmed by in vivo studies (ARC, 1980). In addition, energetic costs associated with eating, ruminating and digestion will decrease the efficiency of ME utilisation still further. Table 1 and Fig. 1 show that the values for B × p vary little around the mean of 0·89. A re-analysis of the original parameter estimates (Blaxter & Boyne, Reference Blaxter and Boyne1978, Appendix 1), showed that the product of B and p (with a mean value of 0·89) was indeed not affected (P = 0·3) by food quality as indicated by q. Therefore, these empirical data are consistent with a maximum partial efficiency of ME utilisation below 100 %.
The rule B × p = 0·89 converts Equation 1 into a one-parameter model, which has advantages, both for the analysis of experimental data and for the use of this equation in modelling. For the analysis of experimental data it provides a much more robust model because estimates for B and p that combine to predict partial efficiencies of more than 100 %, such as happened for some foods depicted in Fig. 1, will no longer occur. For modelling purposes, the rule obviously simplifies the manner in which the effects of food quality and animal state on the relationship between MEI and NEI can be quantified.
The protein module
Since Equation 4 is essentially an energy metabolism model, a module describing the animal in terms of protein or lean growth had to be added. Successful growth models to describe maximum (protein) gains for a variety of species, including sheep (e.g. Jones et al. Reference Jones, Amer, Lewis and Emmans2004), have made use of the Gompertz curve (Emmans, Reference Emmans1997), for which two curve parameters are essential. The parameter value selected for mature protein size (A = 11 kg) was similar to those used before for sheep of similar genotypes (e.g. Jones et al. Reference Jones, Amer, Lewis and Emmans2004). Across species, the rate parameter C relates to A as: C = 0·023 × A − 0·27 (Emmans, Reference Emmans1997). For A = 11 this results in the estimate C = 0·012. Preliminary analysis showed that the use of these parameters resulted in lean weights for pellet-fed lambs that were considerably higher than those experimentally observed. Parameter C was, therefore, set at a value of 0·008 because this resulted in a realistic description of observed lean weights for the pellet-fed sheep. To check whether this was unique for the present data set, we fitted a Gompertz curve to the long-term data presented by Blaxter et al. (Reference Blaxter, Fowler and Gill1982) and Hou (Reference Hou1991). In these long-term experiments, sheep had access ad libitum to high-quality pelleted foods that allowed an accurate estimate of mature size of the sheep. Also for these data sets, the estimated values for parameter C were much lower (20–40 %) than the C value calculated from their A according to the interspecies mean. This suggests that the value of C for sheep may be lower than the interspecies mean. We concluded that the observed lean weights of the pellet-fed animals could only be described accurately by using a corrected C value that was similar to values derived from other long-term data sets obtained with sheep.
For the simulation model it was assumed that lambs would use all the MP that was consumed above maintenance requirements to deposit protein as long as this did not exceed maximum lean and wool growth rate. Since food P supplied liberal amounts of MP, the Gompertz curve determined lean gain of lambs receiving P. However, the MP supplied by the hay generally limited lean gain of lambs consuming hay to lower levels than allowed by the Gompertz curve for a considerable part of the experiment. Lambs could, and in some treatment weeks were predicted to, gain lean body mass while being in a negative energy balance, as has been observed in practice before (Fattet et al. Reference Fattet, De Hovell, Orskov, Kyle, Pennie and Smart1984).
Model predictions
Predictions of food intake
If specific signals from adipocytes increase with lipid reserves and have their effects in the lean part of the animal's body, the lipid/lean ratio may be the best indicator of animal fatness for intake predictions. Estimated B values for the P and H foods varied linearly with lipid/lean ratios and we found no evidence that the slope of the regression lines was affected by food quality (Fig. 4(a)). Lambs in treatments H, P45H and H45P, of which hay intakes were predicted, had average lipid/lean ratios that were lower for much of the observation period than lambs in the treatments that supplied the B estimates. In addition, the FBW of lambs consuming hay in treatments H and P45H were lower throughout the observation period than lambs in P65H that supplied the B estimates for hay. Despite this, intakes were predicted quite accurately.
The data in Fig. 3(b) show that for animals consuming hay in which the lipid/lean ratio exceeded 0·57, corresponding to a CS of 3·6, this ratio ceased to affect estimated B values. The data do not suggest a curvilinear relationship between B and lipid/lean ratios for hay but, instead, a ‘broken-stick’ type of relationship. At present it is not clear what the cause of such a relationship could be, nor if similar breaks occur in the relationships between B estimates and lipid/lean ratio for other (intermediate) food qualities.
Simulation modelling of lamb performance
Equation 4 predicts NEI as well as MEI, i.e. this takes account of differences in efficiency of ME utilisation. Extending the comparison between observations and predictions from FI alone to animal performance can then provide a much stronger test of the hypothesis that energetic efficiency affects energy intake.
The simulations of body weight and CS of lambs were quite accurate (Fig. 5), with only a few exceptions. Lambs in treatment P65H consuming hay were predicted to first lose, then gain, some weight while in reality their weights were almost constant (Fig. 5(a)). Predicted FBW of lambs in treatments H and P45H were higher than observations during the last 10 weeks. This is likely to be related to shearing in week 40. Even though wool weights were added to FBW during this period, there was clearly a drop in FBW just after week 40 which was related to a decrease in hay intake in these groups immediately following shearing (see Figs. 5(a) and 2(c)). A decrease in FI in the first weeks after shearing has been observed before (Hou, Reference Hou1991; BJ Tolkamp, unpublished results). Lambs in treatments H and P45H continued to gain weight after the decrease in FBW following shearing but the simulation model did not take this intake check into account and, consequently, overestimated FBW in this period.
Changes in CS were predicted quite accurately for all treatments except P95H for which the CS was somewhat over-predicted. Simulated CS were calculated from the rule derived from a re-analysis of Russel et al.'s (Reference Russel, Doney and Gunn1969) data and we are confident that this rule gives an adequate relationship between the lipid content in the ffEBW and CS over most of the CS range in this experiment. However, condition scoring cannot detect an increase in animal fatness after sheep have reached a CS of 5. Several animals in treatment P95H reached a CS of 5 several weeks before they were switched to hay in experimental week 40. These animals continued to gain weight during the last weeks they consumed P and it seems very likely that also their fatness continued to increase. However, these animals continued to be scored at 5, which is the upper limit of the scale. As a result, the group-mean CS in this treatment during this period probably underestimated the real average level of lipid reserves in these animals.
Extrapolating the simulation model
Even models that accurately predict observed changes in intake and performance for a given data set can be based on rules that result in predictions that must be considered as implausible when these models are extrapolated to conditions not encountered in the experiment (Parks, Reference Parks1982; Emmans & Kyriazakis, Reference Emmans and Kyriazakis1995). Extrapolation can be used, therefore, to falsify models, although reasonable predictions beyond the range of observations are no proof that the model assumptions are sound. Our simulation model predicted that, in the long run, FBW as well as body lipid content will approach asymptotes. Asymptotes are part of the input data in virtually all growth models (e.g. Parks, Reference Parks1982; Ferguson, Reference Ferguson, Gous, Morris and Fisher2006). However, although the model developed here was based on an asymptote to describe final lean body mass, no asymptote for lipid mass or FBW was defined. That lipid mass and FBW do approach asymptotes, and the value of these asymptotes, are, therefore, predictions of the model itself.
The model predicted that animals receiving hay or pellets only will reach, after several years, the same lean mass but different final FBW of 77 and 118 kg, respectively. This difference is almost entirely the result of differences in predicted final lipid mass. Body lipid content of ewes consuming pellets was predicted to increase as long as animals gain weight. This increase caused a continuous decrease in energetic efficiency as measured by parameter B. This, in turn, affected NEI negatively until it was equal to NEm and both FBW and lipid content in the ffEBW stabilised. In contrast, the body lipid content of ewes consuming hay was predicted to first decrease for about 1 year (as indeed observed during the present experiment) but then to increase again. This is a result of the manner in which the model partitions energy. When hay-fed lambs had a relatively low lean body mass, energy was primarily retained in the form of protein and little in the form of lipid, which caused a gradual decline in lipid/lean ratio in the body. This affected NEI positively via its effect on the value of B. As animals were approaching their mature protein mass, daily protein retention decreased and lipid retention increased. This increased the lipid/lean ratio, which caused NEI to gradually decrease to NEm and then FBW and body lipid content approached their asymptotic value. According to our model, therefore, animals fed hay of the type used will never achieve the same FBW and lipid content that is achieved by animals consuming high-quality pellets.
FBW of around 120 kg have been recorded before in sheep with long-term access to high-quality food (e.g. Blaxter et al. Reference Blaxter, Fowler and Gill1982). Observed lipid contents in the EBW of these animals were indeed between 50 and 60 %, as predicted by our model. We do not know of data sets that recorded FBW and CS of ewes fed the same quality of hay for many years but practical experience suggests that ewes can indeed be fed medium-quality hay for long periods without becoming overly fat. The predictions certainly seem to be within the range of expectations.
Biological implications
In our model, lipid reserves act as a feedback mechanism, via energetic efficiency, on intake relative to maintenance. Sheep consuming high-quality foods, associated with high energetic efficiencies, will deposit high levels of lipid reserves and will defend these once these have reached their asymptotic level. In contrast, animals consuming hay of a quality used in the present experiment will not attain very high levels of lipid reserves, and fat animals will not defend extensive lipid reserves when they have access only to poorer-quality foods associated with lower energetic efficiencies. This was predicted by the model and was observed in the sheep data. This is consistent with observations in other species. Rats with access to normal laboratory chow show modest gains and, in time, will reach a stable body weight at a given lipid content (Mela & Rogers, Reference Mela and Rogers1998). When they have access, in addition to the lab chow, to foods the energy of which can be incorporated efficiently into body reserves (such as fat, peanuts, etc.) they gain weight faster and, in time, reach a higher stable body weight with a much higher lipid content. However, when such animals are then returned to lab chow, the accumulated lipid is not defended. Instead, intake is initially so low that lipid is mobilised rapidly until the lipid reserves approach a level that is typical for animals consuming lab chow (Mela & Rogers, Reference Mela and Rogers1998).
Such mechanisms may well be the result of an evolutionary history in which animals may have been confronted with variation (e.g. seasonal) in food quality. When food quality is high in terms of energetic efficiency, animals may benefit from high energy intakes and deposition of reserves because of the low costs associated with such NE gain. In contrast, animals may deposit little lipid or even mobilise it in other seasons when, in terms of energy expenditure, procurement of NE or the defence of existing NE reserves is costly. That was the underlying idea of the model of Tolkamp & Ketelaars (Reference Tolkamp and Ketelaars1992) to explain variation in intake due to variation in food quality. The present paper extends this approach to take account of the effects of existing reserves on intake and performance. The value of a given food for a given animal may depend upon its state of fatness. Additional lipid reserves may be more valuable for animals with a low lipid/lean ratio than for very fat animals. The leaner animal, therefore, would benefit more from higher intakes than the fat animal when it has access to high-quality food. The model developed in the present paper is consistent with this view.
Acknowledgements
This work was supported by a Scottish Executive Environment and Rural Affairs Department Flexible Fund grant to the Scottish Agricultural College, the University of Edinburgh, the Macaulay Institute and the Rowett Research Institute. The authors are grateful to David Anderson, Terry McHale and Lesley Deans for expert care of experimental animals and data collection.









