In this survey we discuss work of Levin and V’yugin on collections of sequences that are non-negligible in the sense that they can be computed by a probabilistic algorithm with positive probability. More precisely, Levin and V’yugin introduced an ordering on collections of sequences that are closed under Turing equivalence. Roughly speaking, given two such collections 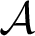$\mathcal {A}$ and 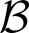$\mathcal {B}$, 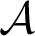$\mathcal {A}$ is below 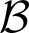$\mathcal {B}$ in this ordering if 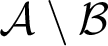$\mathcal {A}\setminus \mathcal {B}$ is negligible. The degree structure associated with this ordering, the Levin–V’yugin degrees (or 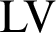$\mathrm {LV}$-degrees), can be shown to be a Boolean algebra, and in fact a measure algebra. We demonstrate the interactions of this work with recent results in computability theory and algorithmic randomness: First, we recall the definition of the Levin–V’yugin algebra and identify connections between its properties and classical properties from computability theory. In particular, we apply results on the interactions between notions of randomness and Turing reducibility to establish new facts about specific LV-degrees, such as the LV-degree of the collection of 1-generic sequences, that of the collection of sequences of hyperimmune degree, and those collections corresponding to various notions of effective randomness. Next, we provide a detailed explanation of a complex technique developed by V’yugin that allows the construction of semi-measures into which computability-theoretic properties can be encoded. We provide two examples of the use of this technique by explicating a result of V’yugin’s about the LV-degree of the collection of Martin-Löf random sequences and extending the result to the LV-degree of the collection of sequences of DNC degree.