Hostname: page-component-54dcc4c588-9xpg2 Total loading time: 0 Render date: 2025-09-26T17:18:58.634Z Has data issue: false hasContentIssue false
  • English
  • Français

The Logic of Bunched Implications

Published online by Cambridge University Press:  15 January 2014

Peter W. O'Hearn  and
David J. Pym
Peter W. O'Hearn
Affiliation:
Department of Computer Science, Queen Mary & Westfield College, University of London London E1 4NS, UK E-mail: ohearn@dcs.qmw.ac.uk
David J. Pym
Affiliation:
Department of Computer Science, Queen Mary & Westfield College, University of London London E1 4NS, UK E-mail: pym@dcs.qmw.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce a logic BI in which a multiplicative (or linear) and an additive (or intuitionistic) implication live side-by-side. The propositional version of BI arises from an analysis of the proof-theoretic relationship between conjunction and implication; it can be viewed as a merging of intuitionistic logic and multiplicative intuitionistic linear logic. The naturality of BI can be seen categorically: models of propositional BI's proofs are given by bicartesian doubly closed categories, i.e., categories which freely combine the semantics of propositional intuitionistic logic and propositional multiplicative intuitionistic linear logic. The predicate version of BI includes, in addition to standard additive quantifiers, multiplicative (or intensional) quantifiers 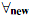and 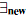which arise from observing restrictions on structural rules on the level of terms as well as propositions. We discuss computational interpretations, based on sharing, at both the propositional and predicate levels.

Information

Type
Research Article
Information
Bulletin of Symbolic Logic , Volume 5 , Issue 2 , June 1999 , pp. 215 - 244
Copyright
Copyright © Association for Symbolic Logic 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

[1] Abramsky, S., Computational interpretations of linear logic, Theoretical Computer Science, vol. 111 (1993), no. 1–2, pp. 3–57.CrossRefGoogle Scholar
[2] Ambler, S., First order linear logic in symmetric monoidal closed categories, Ph.D. thesis , University of Edinburgh, 1992.Google Scholar
[3] Anderson, A. R. and Belnap, N. D., Entailment: the logic of relevance and necessity, volume I, Princeton University Press, 1975.Google Scholar
[4] Anderson, A. R., Dunn, J. M., and Belnap, N. D., Entailment: the logic of relevance and necessity, vol. II, Princeton University Press, 1992.Google Scholar
[5] Barber, A. and Plotkin, G. D., Dual intuitionistic linear logic, submitted, 10 1997.Google Scholar
[6] Belnap, N. D., Display logic, Journal of Philosophical Logic, vol. 11 (1982), pp. 375–414.Google Scholar
[7] Belnap, N. D., Life in the undistributed middle, Substructural logics (Došen, K. and Schroeder-Heister, P., editors), Oxford University Press, 1993, pp. 31–42.CrossRefGoogle Scholar
[8] Benton, P.N., A mixed linear and non-linear logic: proofs, terms and models, Proceedings of computer science logic '94, Kazimierz, Poland, Lecture Notes in Computer Science, no. 933, Springer-Verlag, Berlin, 1995.Google Scholar
[9] Brookes, S., Main, M., Melton, A., and Mislove, M. (editors), Mathematical foundations of programming semantics, eleventh annual conference, Electronic Notes in Theoretical Computer Science, vol. 1, Elsevier Science, 1995, Tulane University, New Orleans, Louisiana.Google Scholar
[10] Day, B. J., On closed categories of functors, Reports of the midwest category seminar (Lane, S.Mac, editor), Lecture Notes in Mathematics, vol. 137, Springer-Verlag, Berlin-New York, 1970, pp. 1–38.Google Scholar
[11] Day, B. J., An embedding theoremfor closed categories, Category seminar, Sydney (Kelly, G.M., editor), Lecture Notes in Mathematics, no. 420, Springer-Verlag, Berlin-New York, 1974, pp. 55–64.Google Scholar
[12] Došsen, K., A historical introduction to substructural logics, Substructural logics (Došsen, K. and Schroeder-Heister, P., editors), Oxford University Press, 1993, pp. 1–30.Google Scholar
[13] Dunn, J. M., Conseqution formulation of positive R with co-tenability and t, in [3].Google Scholar
[14] Dunn, J. M., Relevant logic and entailment, Handbook of philosophical logic (Gabbay, D. and Guenthner, F., editors), vol. III: Alternatives in Classical Logic, Synthese Library, no. 166, D. Reidel, Dordrecht, Holland, 1986, pp. 117–224.Google Scholar
[15] Girard, J.-Y., Linear logic, Theoretical Computer Science, vol. ? (1987), pp. 1–102.Google Scholar
[16] Girard, J.-Y., On the unity of logic, Annals of Pure and Applied Logic, vol. 59 (1993), pp. 201–217.Google Scholar
[17] Harland, J. A., Pym, D. J., and Winikoff, M., Programming in Lygon: an overview, Proceedings of AMAST '96 (Berlin) (Wirsing, M. and Nivat, M., editors), Lecture Notes in Computer Science, no. 1101, Springer-Verlag, 1996, pp. 391–405.Google Scholar
[18] Hodas, J. S. and Miller, D., Logic programming in a fragment of intuitionistic linear logic, Information and Computation, vol. 110 (1994), no. 2, pp. 327–365.Google Scholar
[19] Ishtiaq, S. S. and Pym, D. J., Kripke resource models of a dependently-typed, bunched λ-calculus, in preparation, available at http://www.dcs.qmw.ac.uk/~pym.Google Scholar
[20] Ishtiaq, S. S. and Pym, D. J., A relevant analysis of natural deduction, Journal of Logic and Computation, vol. 8 (1998), no. 6, pp. 809–838.Google Scholar
[21] Kleene, S. C., Mathematical logic, Wiley and Sons, 1968.Google Scholar
[22] Kripke, S. A., Semantical analysis of intuitionistic logic I, Formal systems and recursive functions (Crossley, J. N. and Dummett, M. A. E., editors), North-Holland, Amsterdam, 1965, pp. 92–130.Google Scholar
[23] Lafont, Y., The linear abstractmachine, Theoretical Computer Science, vol. 59 (1988), pp. 157–180.CrossRefGoogle Scholar
[24] Lambek, J. and Scott, P. J., Introduction to higher-order categorical logic, Cambridge University Press, Cambridge, England, 1986.Google Scholar
[25] Martin-Löf, P., On the meanings of the logical constants and the justifications of the logical laws, Technical Report 2, Scuola di Specializziazione in Logica Matematica, Universitàa di Siena, 1982.Google Scholar
[26] Miller, D., A logical analysis of modules in logic programming, Journal of Logic Programming, vol. 6 (1989), no. 1 and 2, pp. 79–108.Google Scholar
[27] Miller, D., Nadathur, G., Pfenning, F., and ščedrov, A., Uniform proofs as a foundation for logic programming, Annals of Pure and Applied Logic, vol. 51 (1991), pp. 125–157.CrossRefGoogle Scholar
[28] O'Hearn, P. W., Resource interpretations, bunched implications and the αλ-calculus, in preparation, preliminary version to appear in Typed λ-calculus and applications, Lecture Notes in Computer Science, 1999.Google Scholar
[29] O'Hearn, P. W., Power, A. J., Takeyama, M., and Tennent, R. D., Syntactic control of interference revisited, to appear in Theoretical Computer Science, preliminary version in [9] and in [30].Google Scholar
[30] O'Hearn, P. W. and Tennent, R. D. (editors), Algol-like languages, Birkhäuser, Boston, 1997, two volumes.Google Scholar
[31] Plotkin, G. D., Type theory and recursion, slides for Scottfest talk, 1993.Google Scholar
[32] Pym, D. J., Logic programming with bunched implications, Electronic Notes in Theoretical Computer Science, vol. 17 (1998), extended abstract, 24 pp.Google Scholar
[33] Pym, D. J., The semantics and proof theory of the logic of bunched implications, II: predicate BI, available on the web at http://www.dcs.qmw.ac.uk/~pym, 1998.Google Scholar
[34] Pym, D. J., The semantics and proof theory of the logic of bunched implications, I: Propositional BI, available on the web at http://www.dcs.qmw.ac.uk/~pym, 1998.Google Scholar
[35] Pym, D. J. and Harland, J. A., A uniform proof-theoretic investigation of linear logic programming, Journal of Logic and Computation, vol. 4 (1994), pp. 175–207.Google Scholar
[36] Read, S., Relevant logic: a philosophical examination of inference, Basil Blackwell, 1987.Google Scholar
[37] Reynolds, J. C., Syntactic control of interference, Conference record of the fifth annual acm symposium on principles of programming languages (New York), ACM, 01 1978, also in [30], pp. 39–46.Google Scholar
[38] Reynolds, J. C., The essence of Algol, Algorithmic languages: Proceedings of the international symposium on algorithmic languages (Amsterdam) (Bakker, J. W. de and Vliet, J. C. van, editors), North-Holland, 10 1981, also in [30], pp. 345–372.Google Scholar
[39] Ruet, P. and Fages, F., Concurrent constraint programming and mixed non-commutative linear logic, Proceedings of CSL '97 (Berlin), Lecture Notes in Computer Science, no. 1414, Springer-Verlag, 1997.Google Scholar
[40] Sacerdoti, E. D., A structure for plans and behaviour, Elsevier North Holland, 1977.Google Scholar
[41] Schroeder-Heister, P., Structural frameworks, substructural logics and the role of elimination inferences, Logical frameworks (Huet, G. and Plotkin, G., editors), Cambridge University Press, 1991, pp. 385–403.Google Scholar
[42] Seely, R. A. G., Linear logic, *-autonomous categories and cofree coalgebras, Categories in computer science and logic (Providence, Rhode Island) (Gray, J. W. and Scedrov, A., editors), Contemporary Mathematics, no. 92, American Mathematical Society, 1989, pp. 371–382.Google Scholar
[43] Troelstra, A. S., Tutorial on linear logic, Substructural logics (Došen, K. and Schroeder-Heister, P., editors), Oxford University Press, 1993, pp. 327–355.CrossRefGoogle Scholar
[44] Urquhart, A., Semantics for relevant logics, this Journal, vol. 49 (1972), pp. 1059–1073.Google Scholar