Article contents
REDUCTION TECHNIQUES FOR PROVING DECIDABILITY IN LOGICS AND THEIR MEET–COMBINATION
Published online by Cambridge University Press: 06 May 2021
Abstract
Satisfaction systems and reductions between them are presented as an appropriate context for analyzing the satisfiability and the validity problems. The notion of reduction is generalized in order to cope with the meet-combination of logics. Reductions between satisfaction systems induce reductions between the respective satisfiability problems and (under mild conditions) also between their validity problems. Sufficient conditions are provided for relating satisfiability problems to validity problems. Reflection results for decidability in the presence of reductions are established. The validity problem in the meet-combination is proved to be decidable whenever the validity problem for the components are decidable. Several examples are discussed, namely, involving modal and intuitionistic logics, as well as the meet-combination of 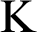 $\textrm {K}$ modal logic and intuitionistic logic.
$\textrm {K}$ modal logic and intuitionistic logic.
MSC classification
Information
- Type
- Articles
- Information
- Copyright
- © The Association for Symbolic Logic 2021
References
REFERENCES
- 1
- Cited by


