Article contents
The Absolute Arithmetic Continuum and the Unification Of all Numbers Great and Small
Published online by Cambridge University Press: 15 January 2014
Abstract
In his monograph On Numbers and Games, J. H. Conway introduced a real-closed field containing the reals and the ordinals as well as a great many less familiar numbers including −ω, ω/2, 1/ω, 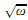 and ω − π to name only a few. Indeed, this particular real-closed field, which Conway calls No, is so remarkably inclusive that, subject to the proviso that numbers—construed here as members of ordered fields—be individually definable in terms of sets of NBG (von Neumann–Bernays–Gödel set theory with global choice), it may be said to contain “All Numbers Great and Small.” In this respect, No bears much the same relation to ordered fields that the system ℝ of real numbers bears to Archimedean ordered fields.
and ω − π to name only a few. Indeed, this particular real-closed field, which Conway calls No, is so remarkably inclusive that, subject to the proviso that numbers—construed here as members of ordered fields—be individually definable in terms of sets of NBG (von Neumann–Bernays–Gödel set theory with global choice), it may be said to contain “All Numbers Great and Small.” In this respect, No bears much the same relation to ordered fields that the system ℝ of real numbers bears to Archimedean ordered fields.
In Part I of the present paper, we suggest that whereas ℝ should merely be regarded as constituting an arithmetic continuum (modulo the Archimedean axiom), No may be regarded as a sort of absolute arithmetic continuum (modulo NBG), and in Part II we draw attention to the unifying framework No provides not only for the reals and the ordinals but also for an array of non-Archimedean ordered number systems that have arisen in connection with the theories of non-Archimedean ordered algebraic and geometric systems, the theory of the rate of growth of real functions and nonstandard analysis.
In addition to its inclusive structure as an ordered field, the system No of surreal numbers has a rich algebraico-tree-theoretic structure—a simplicity hierarchical structure—that emerges from the recursive clauses in terms of which it is defined. In the development of No outlined in the present paper, in which the surreals emerge vis-à-vis a generalization of the von Neumann ordinal construction, the simplicity hierarchical features of No are brought to the fore and play central roles in the aforementioned unification of systems of numbers great and small and in some of the more revealing characterizations of No as an absolute continuum.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2012
References
REFERENCES
- 41
- Cited by

