Article contents
AN ABSTRACT ALGEBRAIC LOGIC STUDY OF DA COSTA’S LOGIC 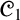 ${\mathscr {C}}_1$ AND SOME OF ITS PARACONSISTENT EXTENSIONS
${\mathscr {C}}_1$ AND SOME OF ITS PARACONSISTENT EXTENSIONS
Published online by Cambridge University Press: 04 October 2022
Abstract
Two famous negative results about da Costa’s paraconsistent logic 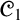 ${\mathscr {C}}_1$ (the failure of the Lindenbaum–Tarski process [44] and its non-algebraizability [39]) have placed
${\mathscr {C}}_1$ (the failure of the Lindenbaum–Tarski process [44] and its non-algebraizability [39]) have placed 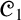 ${\mathscr {C}}_1$ seemingly as an exception to the scope of Abstract Algebraic Logic (AAL). In this paper we undertake a thorough AAL study of da Costa’s logic
${\mathscr {C}}_1$ seemingly as an exception to the scope of Abstract Algebraic Logic (AAL). In this paper we undertake a thorough AAL study of da Costa’s logic 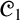 ${\mathscr {C}}_1$. On the one hand, we strengthen the negative results about
${\mathscr {C}}_1$. On the one hand, we strengthen the negative results about 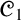 ${\mathscr {C}}_1$ by proving that it does not admit any algebraic semantics whatsoever in the sense of Blok and Pigozzi (a weaker notion than algebraizability also introduced in the monograph [6]). On the other hand,
${\mathscr {C}}_1$ by proving that it does not admit any algebraic semantics whatsoever in the sense of Blok and Pigozzi (a weaker notion than algebraizability also introduced in the monograph [6]). On the other hand, 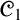 ${\mathscr {C}}_1$ is a protoalgebraic logic satisfying a Deduction-Detachment Theorem (DDT). We then extend our AAL study to some paraconsistent axiomatic extensions of
${\mathscr {C}}_1$ is a protoalgebraic logic satisfying a Deduction-Detachment Theorem (DDT). We then extend our AAL study to some paraconsistent axiomatic extensions of 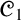 ${\mathscr {C}}_1$ covered in the literature. We prove that for extensions
${\mathscr {C}}_1$ covered in the literature. We prove that for extensions 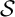 ${\mathcal {S}}$ such as
${\mathcal {S}}$ such as 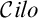 ${\mathcal {C}ilo}$ [26], every algebra in
${\mathcal {C}ilo}$ [26], every algebra in 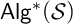 ${\mathsf {Alg}}^*({\mathcal {S}})$ contains a Boolean subalgebra, and for extensions
${\mathsf {Alg}}^*({\mathcal {S}})$ contains a Boolean subalgebra, and for extensions 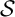 ${\mathcal {S}}$ such as
${\mathcal {S}}$ such as 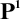 ,
, 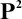 , or
, or 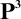 [16, 53], every subdirectly irreducible algebra in
[16, 53], every subdirectly irreducible algebra in 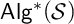 ${\mathsf {Alg}}^*({\mathcal {S}})$ has cardinality at most 3. We also characterize the quasivariety
${\mathsf {Alg}}^*({\mathcal {S}})$ has cardinality at most 3. We also characterize the quasivariety 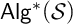 ${\mathsf {Alg}}^*({\mathcal {S}})$ and the intrinsic variety
${\mathsf {Alg}}^*({\mathcal {S}})$ and the intrinsic variety 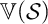 $\mathbb {V}({\mathcal {S}})$, with
$\mathbb {V}({\mathcal {S}})$, with 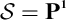 ,
, 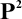 , and
, and 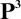 .
.
Information
- Type
- Articles
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic
References
- 3
- Cited by


