Hostname: page-component-848d4c4894-m9kch Total loading time: 0 Render date: 2024-05-18T04:57:28.526Z Has data issue: false hasContentIssue false
  • English
  • Français

Arguments for the Continuity Principle

Published online by Cambridge University Press:  15 January 2014

Mark van Atten  and
Dirk van Dalen
Mark van Atten
Affiliation:
Institute of Philosophy, Kuleuven, Belgium, E-mail: mark.vanatten@hiw.kuleuven.ac.be
Dirk van Dalen
Affiliation:
Department of Philosophy, Utrecht University, The Netherlands, E-mail: dirk.vandalen@phil.uu.nl
Get access Rights & Permissions [Opens in a new window]

Extract

There are two principles that lend Brouwer's mathematics the extra power beyond arithmetic. Both are presented in Brouwer's writings with little or no argument. One, the principle of bar induction, will not concern us here. The other, the continuity principle for numbers, occurs for the first time in print in [4]. It is formulated and immediately applied to show that the set of numerical choice sequences is not enumerable. In fact, the idea of the continuity property can be dated fairly precisely, it is to be found in the margin of Brouwer's notes for his course on Pointset Theory of 1915/16. The course was repeated in 1916/17 and he must have inserted his first formulation of the continuity principle in the fall of 1916 as new material right at the beginning of the course.

In modern language, the principle reads

where α and β range over choice sequences of natural numbers, m and x over natural numbers, and 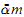stands for ⟨α(0), α(1), …, α(m − 1)⟩, the initial segment of α of length m.

An immediate consequence of WC-N is that all full functions are continuous, and, as a corollary, that the continuum is unsplittable [28]. Note that WC-N is incompatible with Church's thesis, [22], section 4.6.

After Brouwer asserted WC-N, Troelstra was the first to ask in print for a conceptual motivation, but he remained an exception; most authors followed Brouwer by simply asserting it, cf. [18].

Let us note first that in one particular case the principle is obvious indeed, namely in the case of the lawless sequences. The notion of lawless sequence surfaced fairly late in the history of intuitionism. Kreisel introduced it in [17] for metamathematical purposes. There is a letter from Brouwer to Heyting in which the phenomenon also occurs [7]. This is an important and interesting fact since it is (probably) the only time that Brouwer made use of a possibility expressly stipulated in, e.g., [5], see below.

Type
Research Article
Information
Bulletin of Symbolic Logic , Volume 8 , Issue 3 , September 2002 , pp. 329 - 347
Copyright
Copyright © Association for Symbolic Logic 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Beeson, M., The nonderivability in intuitionistic formal systems of theorems on the continuity of effective operations, The Journal of Symbolic Logic, vol. 40 (1975), pp. 321–346.CrossRefGoogle Scholar
[2] Beeson, M., Foundations of constructive mathematics, Springer, 1985.Google Scholar
[3] Bridges, D., van Dalen, D., and Ishihara, H., How to understand Ishihara's tricks, preprint, Christchurch, NZ.Google Scholar
[4] Brouwer, L. E. J., Begründung der Mengenlehre unabhängig vom logischen Satz vom ausgeschlossenen Dritten, Erster Teil, Allgemeine Mengenlehre, Koninklijke Nederlandse Akademie van Wetenschschappen Verhandelingen, vol. 5 (1918), pp. 1–43.Google Scholar
[5] Brouwer, L. E. J., Zur Begründung der intuitionistischen Mathematik I, Mathematische Annalen, vol. 93 (1925), pp. 244–257.Google Scholar
[6] Brouwer, L. E. J., Über Definitionsbereiche von Funktionen, Mathematische Annalen, vol. 97 (1927), pp. 60–75.CrossRefGoogle Scholar
[7] Brouwer, L. E. J., Zum freien Werden von Mengen und Funktionen, Indagationes Mathematicae, vol. 4 (1942), pp. 107–108.Google Scholar
[8] Brouwer, L. E. J., Richtlijnen der intuitionistische wiskunde, Indagationes Mathematicae, vol. 9 (1947), p. 197, Quoted from translation ‘Guidelines of intuitionistic mathematics’ [10, p. 477].Google Scholar
[9] Brouwer, L. E. J., Historical background, principles and methods of intuitionism, South African Journal of Science, vol. 49 (1952), pp. 139–146.Google Scholar
[10] Brouwer, L. E. J., Collected works I. Philosophy and foundations of mathematics, (A. Heyting, editor), North-Holland, 1975.Google Scholar
[11] Brouwer, L. E. J., Brouwer's Cambridge lectures on intuitionism, (D. van Dalen, editor), Cambridge University Press, 1981.Google Scholar
[12] Husserl, E., Ideen zu einer reinen Phänomenologie und phänomenologischen Philosophie. Erstes Buch, Husserliana, vol. III/1, Martinus Nijhoff, 1976.Google Scholar
[13] Ishihara, H., Continuity and nondiscontinuity in constructive mathematics, The Journal of Symbolic Logic, vol. 56 (1991), pp. 1349–1354.Google Scholar
[14] Ishihara, H., Continuity properties in constructive mathematics, The Journal of Symbolic Logic, vol. 57 (1992), pp. 557–565.Google Scholar
[15] Kreisel, G., A remark on free choice sequences and the topological completeness proofs, The Journal of Symbolic Logic, vol. 23 (1958), pp. 369–388.Google Scholar
[16] Kreisel, G., Informal rigour and completeness proofs, Problems in the philosophy of mathematics (Lakatos, I., editor), North-Holland, 1967, pp. 138–186.Google Scholar
[17] Kreisel, G., Lawless sequences of natural numbers, Compositio Mathematica, vol. 20 (1968), pp. 222–248.Google Scholar
[18] Troelstra, A. S., Choice sequences. A chapter of intuitionistic mathematics, Oxford University Press, 1977.Google Scholar
[19] Troelstra, A. S., Analysing choice sequences, Journal of Philosophical Logic, vol. 12 (1983), pp. 197–260.Google Scholar
[20] Troelstra, A. S., Choice sequences and informal rigour, Synthese, vol. 62 (1985), pp. 217–227.CrossRefGoogle Scholar
[21] Troelstra, A. S. and van Dalen, D., Projections of lawless sequences, Intuitionism and proof theory (Myhill, J., Kino, A., and Vesley, R. E., editors), North-Holland, 1970, pp. 163–186.Google Scholar
[22] Troelstra, A. S. and van Dalen, D., Constructivism in mathematics, I, II, North-Holland, 1988.Google Scholar
[23] van Atten, M., Phenomenology of choice sequences, Ph.D. thesis , Utrecht University, 1999.Google Scholar
[24] van Atten, M., van Dalen, D., and Tieszen, R., Brouwer and Weyl: The phenomenology and mathematics of the intuitive continuum, Philosophia Mathematica, (Forthcoming).Google Scholar
[25] van Dalen, D., Hermann Weyl's intuitionistic mathematics, this Bulletin, vol. 1 (1995), pp. 145–169.Google Scholar
[26] van der Hoeven, G., Projections of lawless sequences, Ph.D. thesis , University of Amsterdam, 1981.Google Scholar
[27] van Heijenoort, J. (editor), From Frege to Gödel: A sourcebook in mathematical logic, 1879–1931, Harvard University Press, 1967.Google Scholar
[28] Veldman, W., On the continuity of functions in intuitionistic real analysis. Some remarks on Brouwer's paper: ‘Über Definitionsbereiche von Funktionen’, Technical Report 8210, Katholieke Universiteit Nijmegen, Mathematisch Instituut, 04 1982.Google Scholar
[29] Weyl, H., Über die neue Grundlagenkrise der Mathematik, Mathematische Zeitschrift, vol. 10 (1921), pp. 39–79.CrossRefGoogle Scholar