Hostname: page-component-8448b6f56d-c4f8m Total loading time: 0 Render date: 2024-04-23T21:56:18.984Z Has data issue: false hasContentIssue false
  • English
  • Français

CHAIN CONDITIONS OF PRODUCTS, AND WEAKLY COMPACT CARDINALS

Published online by Cambridge University Press:  24 October 2014

ASSAF RINOT
ASSAF RINOT*
Affiliation:
DEPARTMENT OF MATHEMATICS, BAR-ILAN UNIVERSITY, RAMAT-GAN 52900, ISRAEL, URL: http://www.assafrinot.comE-mail: rinotas@math.biu.ac.il
Get access Rights & Permissions [Opens in a new window]

Abstract

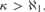The history of productivity of the κ-chain condition in partial orders, topological spaces, or Boolean algebras is surveyed, and its connection to the set-theoretic notion of a weakly compact cardinal is highlighted. Then, it is proved that for every regular cardinal $\kappa > \aleph _1 {\rm{,}}$ the principle □(k) is equivalent to the existence of a certain strong coloring $c\,:\,[k]^2 \, \to $k for which the family of fibers ${\cal T}\left( c \right)$ is a nonspecial κ-Aronszajn tree.

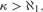The theorem follows from an analysis of a new characteristic function for walks on ordinals, and implies in particular that if the κ-chain condition is productive for a given regular cardinal $\kappa > \aleph _1 {\rm{,}}$ then κ is weakly compact in some inner model of ZFC. This provides a partial converse to the fact that if κ is a weakly compact cardinal, then the κ-chain condition is productive.

Keywords

Aronszajn treechain conditionsquarewalks on ordinalsweakly compact cardinal
Type
Articles
Information
Bulletin of Symbolic Logic , Volume 20 , Issue 3 , September 2014 , pp. 293 - 314
Copyright
Copyright © The Association for Symbolic Logic 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[Alv99] Alvarez, Carlos, On the history of Souslin’s problem. Archive for History of Exact Sciences, vol. 54 (1999), no. 3, pp. 181–242.Google Scholar
[ARS85] Abraham, Uri, Rubin, Matatyahu, and Shelah, Saharon, On the consistency of some partition theorems for continuous colorings, and the structure ℵ1 of -dense real order types. Annals of pure and applied logic, vol. 29 (1985), no. 2, pp. 123–206.Google Scholar
[AS81] Avraham, Uri and Shelah, Saharon, Martin’s axiom does not imply that every two ℵ1 -dense sets of reals are isomorphic. Israel Journal of Mathematics, vol. 38 (1981), pp. 161–176.Google Scholar
[Bau73] Baumgartner, James E., All ℵ1 -dense sets of reals can be isomorphic. Fundamenta Mathematicae, vol. 79 (1973), no. 2, pp. 101–106.Google Scholar
[Bau76] Baumgartner, James E., A new class of order types. Annals of Mathematics Logic, vol. 9 (1976), no. 3, pp. 187–222.CrossRefGoogle Scholar
[Bla72] Blass, Andreas, Weak partition relations. Proceedings of the American Mathematical Society, vol. 35 (1972), pp. 249–253.CrossRefGoogle Scholar
[BMR70] Baumgartner, J., Malitz, J., and Reinhardt, W., Embedding trees in the rationals. Proceedings of the National Academy of Sciences, U.S.A, vol. 67 (1970), pp. 1748–1753.Google Scholar
[BS85] Bonnet, Robert and Shelah, Saharon, Narrow boolean algebras. Annals of Pure and Applied Logic, vol. 28 (1985), pp. 1–12.Google Scholar
[Coh64] Cohen, Paul J., The independence of the continuum hypothesis. II. Proceedings of the National Academy of Sciences, U.S.A, vol. 51 (1964), pp. 105–110.Google Scholar
[EHMR84] Erdős, Paul, Hajnal, András, Máté, Attila, and Rado, Richard, Combinatorial set theory: partition relations for cardinals, Studies in Logic and the Foundations of Mathematics, vol. 106, North-Holland Publishing Co., Amsterdam, 1984.Google Scholar
[EHR65] Erdős, P., Hajnal, A., and Rado, R., Partition relations for cardinal numbers. Acta Mathematica Academiae Scientiarum Hungaricae, vol. 16 (1965), pp. 93–196.Google Scholar
[Eis10] Eisworth, Todd, Club-guessing, stationary reflection, and coloring theorems. Annals of pure and applied logic, vol. 161 (2010), no. 10, pp. 1216–1243.CrossRefGoogle Scholar
[Eis13] Eisworth, Todd, Getting more colors II. Journal of Symbolic Logic, vol. 78 (2013), no. 1, pp. 17–38.Google Scholar
[ET43] Erdös, P. and Tarski, A, On families of mutually exclusive sets. Annals of Mathematics (2), vol. 44 (1943), pp. 315–329.Google Scholar
[Fle78] Fleissner, William G., Some spaces related to topological inequalities proven by the Erdős-Rado theorem. Proceedings of the American Mathematical Society, vol. 71 (1978), no. 2, pp. 313–320.Google Scholar
[Fre84] Fremlin, D. H., Consequences of Martin’s axiom, Cambridge Tracts in Mathematics, vol. 84, Cambridge University Press, Cambridge, 1984.Google Scholar
[Gal80] Galvin, Fred, Chain conditions and products. Fundamenta Mathematicae, vol. 108 (1980), no. 1, pp. 33–48.CrossRefGoogle Scholar
[GS73] Galvin, Fred and Shelah, Saharon, Some counterexamples in the partition calculus. Journal of Combinatorial Theory, Series A, vol. 15 (1973), pp. 167–174.Google Scholar
[Jen72] Björn Jensen, R., The fine structure of the constructible hierarchy. Annals of Mathematical Logic, vol. 4 (1972), pp. 229–308; erratum, ibid. 4(1972), 443, With a section by Jack Silver.Google Scholar
[Jen14] Björn Jensen, R., personal communcation, June(2014).Google Scholar
[Juh80] Juhász, István, Cardinal functions in topology—ten years later, second edition, Mathematical Centre Tracts, vol. 123, Mathematisch Centrum, Amsterdam, 1980.Google Scholar
Kanamori, Akihiro, Historical remarks on Suslin’s problem, Set theory, arithmetic, and foundations of mathematics: theorems, philosophies, Lect. Notes Log., vol. 36, Association of Symbolic Logic, La Jolla, CA, 2011, pp. 1–12.Google Scholar
[KLMV08] König, Bernhard, Larson, Paul, Moore, Justin Tatch, and Veličković, Boban, Bounding the consistency strength of a five element linear basis, Israel Journal of Mathematics, vol. 164 (2008), pp. 1–18.CrossRefGoogle Scholar
[Kop89] Koppelberg, Sabine, Handbook of Boolean algebras. Vol. 1 (Donald Monk, J. and Bonnet, Robert, editors), North-Holland Publishing Co., Amsterdam, 1989.Google Scholar
[Kru13] Krueger, John, Weak square sequences and special Aronszajn trees, Fundamenta Mathematicae, vol. 221 (2013), no. 3, pp. 267–284.CrossRefGoogle Scholar
[KS93] Kojman, Menachem and Shelah, Saharon, μ-complete Souslin trees on μ 1, Archive for Mathematical Logic, vol. 32 (1993), no. 3, pp. 195–201.Google Scholar
[Kun78] Kunen, Kenneth, Saturated ideals. Journal of Symbolic Logic, vol. 43 (1978), no. 1, pp. 65–76.Google Scholar
[Kur52] Kurepa, Djuro, Sur une propriété caractéristique du continu linéaire et le problème de Suslin. Academie Serbe des Sciences, Publications de l’Institut Mathematique, vol. 4 (1952), pp. 97–108.Google Scholar
Kurepa, Djuro, The Cartesian multiplication and the cellularity number. Publications de l’Institut Mathematique (Beograd) (N.S.), vol. 2 (1963), no. 16, pp. 121–139.Google Scholar
[LS81] Laver, Richard and Shelah, Saharon, The ℵ2-souslin hypothesis. Transactions of the American Mathematical Society, vol. 264 (1981), pp. 411–417.Google Scholar
[Mag82] Magidor, Menachem, Reflecting stationary sets. Journal of Symbolic Logic, vol. 47 (1982), no. 4, pp. 755–771 (1983).CrossRefGoogle Scholar
[Mar47] Marczewski, Edward, Séparabilité et multiplication cartésienne des espaces topologiques. Fundamenta Mathematicae, vol. 34 (1947), pp. 127–143.Google Scholar
[Mit73] Mitchell, William, Aronszajn trees and the independence of the transfer property. Annals of Mathematical Logic, vol. 5 (1972/73), pp. 21–46.CrossRefGoogle Scholar
[Mon14] Donald Monk, J., Cardinal invariants on Boolean algebras, revised edition, Progress in Mathematics, vol. 142, Birkhäuser/Springer, Basel, 2014.CrossRefGoogle Scholar
[Moo06] Moore, Justin Tatch, A five element basis for the uncountable linear orders. Annals of Mathematics (2), vol. 163 (2006), no. 2, pp. 669–688.CrossRefGoogle Scholar
[Rin11] Rinot, Assaf, Jensen’s diamond principle and its relatives, Set theory and its applications, Contemporary Mathematics, vol. 533, American Mathematical Society, Providence, RI, 2011, pp. 125–156.CrossRefGoogle Scholar
[Rin12] Rinot, Assaf, Transforming rectangles into squares, with applications to strong colorings. Advances in Mathematics, vol. 231 (2012), no. 2, pp. 1085–1099.CrossRefGoogle Scholar
[Rin14a] Rinot, Assaf, Complicated colorings, (2014), pp. 1–13, submitted January 2014.Google Scholar
[Rin14b] Rinot, Assaf, The Ostaszewski square, and homogeneous Souslin trees. Israel Journal of Mathematics, vol. 199 (2014), no. 2, pp. 975–1012.CrossRefGoogle Scholar
[Roi78] Roitman, Judy, A reformulation of S and L. Proceedings of the American Mathematical Society, vol. 69 (1978), no. 2, pp. 344–348.Google Scholar
[Roy89] Roy, Nina M., Is the product of ccc spaces a ccc space?. Publicacions Matematiques, vol. 33 (1989), no. 2, pp. 173–183.Google Scholar
[She78] Shelah, Saharon, Jonsson algebras in successor cardinals. Israel Journal of Mathematics, vol. 30 (1978), pp. 57–64.Google Scholar
Shelah, Saharon, Successors of singulars, cofinalities of reduced products of cardinals and productivity of chain conditions. Israel Journal of Mathematics, vol. 62 (1988), pp. 213–256.CrossRefGoogle Scholar
[She88b] Shelah, Saharon, Was sierpiński right? I. Israel Journal of Mathematics, vol. 62 (1988), pp. 355–380.CrossRefGoogle Scholar
[She90] Shelah, Saharon, Strong negative partition above the continuum. The Journal of Symbolic Logic, vol. 55 (1990), pp. 21–31.Google Scholar
[She91] Shelah, Saharon, Strong negative partition relations below the continuum. Acta Mathematica Hungarica, vol. 58 (1991), pp. 95–100.CrossRefGoogle Scholar
[She94a] Shelah, Saharon, $\aleph _{\omega + 1} $has a jonsson algebra, Cardinal arithmetic, Oxford Logic Guides, vol. 29, Oxford University Press, 1994.Google Scholar
[She94b] Shelah, Saharon, There are jonsson algebras in many inaccessible cardinals. Cardinal arithmetic, Oxford Logic Guides, vol. 29, Oxford University Press, 1994.Google Scholar
[She97] Shelah, Saharon, Colouring and non-productivity of ℵ2 -cc. Annals of Pure and Applied Logic, vol. 84 (1997), pp. 153–174.Google Scholar
[Sie33] Sierpiński, Waclaw, Sur un problème de la théorie des relations. Annali della Scuola Normale Superiore di Pisa - Classe di Scienze (2), vol. 2 (1933), no. 3, pp. 285–287.Google Scholar
[Spe49] Specker, E., Sur un problème de Sikorski. Colloquium Mathematicum, vol. 2 (1949), pp. 9–12.Google Scholar
[SS88] Shelah, Saharon and Stanley, Lee, Weakly compact cardinals and nonspecial Aronszajn trees. Proceedings of the American Mathematical Society, vol. 104 (1988), no. 3, pp. 887–897.CrossRefGoogle Scholar
[Tod84] Todorčević, Stevo, A note on the proper forcing axiom, Axiomatic set theory (Boulder, Colo., 1983), Contemporary Mathematics, vol. 31, American Mathematical Society, Providence, RI, 1984, pp. 209–218.CrossRefGoogle Scholar
[Tod85] Todorčević, Stevo, Remarks on chain conditions in products. Compositio Mathematica, vol. 55 (1985), no. 3, pp. 295–302.Google Scholar
[Tod86] Todorčević, Stevo, Remarks on cellularity in products. Compositio Mathematica, vol. 57 (1986), no. 3, pp. 357–372.Google Scholar
[Tod87] Todorčević, Stevo, Partitioning pairs of countable ordinals. Acta Mathematica, vol. 159 (1987), no. 3–4, pp. 261–294.Google Scholar
[Tod88] Todorčević, Stevo, Oscillations of real numbers, Logic colloquium ’86 (Hull, 1986), Studies in Logic and the Foundations of Mathematics, vol. 124, North-Holland, Amsterdam, 1988, pp. 325–331.Google Scholar
[Tod89a] Todorčević, Stevo, Partition problems in topology, Contemporary Mathematics, vol. 84, American Mathematical Society, Providence, RI, 1989.Google Scholar
[Tod89b] Todorčević, Stevo, Special square sequences. Proceedings of the American Mathematical Society, vol. 105 (1989), no. 1, pp. 199–205.Google Scholar
Todorčević, Stevo, Oscillations of sets of integers. Advances in Applied Mathematics, vol. 20 (1998), no. 2, pp. 220–252.CrossRefGoogle Scholar
[Tod07] Todorčević, Stevo, Walks on ordinals and their characteristics, Progress in Mathematics, vol. 263, Birkhäuser Verlag, Basel, 2007.Google Scholar
[Vel86] Veličković, Boban, Jensen’s □ principles and the Novák number of partially ordered sets. Journal of Symbolic Logic, vol. 51 (1986), no. 1, pp. 47–58.Google Scholar
[Vel92] Todorčević, Stevo, Forcing axioms and stationary sets. Advances in Mathematics, vol. 94 (1992), no. 2, pp. 256–284.Google Scholar