Article contents
Definability in the Recursively Enumerable Degrees
Published online by Cambridge University Press: 15 January 2014
Extract
§1. Introduction. Natural sets that can be enumerated by a computable function (the recursively enumerable or r.e. sets) always seem to be either actually computable (recursive) or of the same complexity (with respect to Turing computability) as the Halting Problem, the complete r.e. set K. The obvious question, first posed in Post [1944] and since then called Post's Problem is then just whether there are r.e. sets which are neither computable nor complete, i.e., neither recursive nor of the same Turing degree as K?
Let 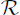 be the r.e. degrees, i.e., the r.e. sets modulo the equivalence relation of equicomputable with the partial order induced by Turing computability. This structure is a partial order (indeed, an uppersemilattice or usl)with least element 0, the degree (equivalence class) of the computable sets, and greatest element 1 or 0′, the degree of K. Post's problem then asks if there are any other elements of
be the r.e. degrees, i.e., the r.e. sets modulo the equivalence relation of equicomputable with the partial order induced by Turing computability. This structure is a partial order (indeed, an uppersemilattice or usl)with least element 0, the degree (equivalence class) of the computable sets, and greatest element 1 or 0′, the degree of K. Post's problem then asks if there are any other elements of 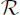 .
.
The (positive) solution of Post's problem by Friedberg [1957] and Muchnik [1956] was followed by various algebraic or order theoretic results that were interpreted as saying that the structure 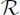 was in some way well behaved:
was in some way well behaved:
Theorem 1.1 (Embedding theorem; Muchnik [1958], Sacks [1963]). Every countable partial ordering or even uppersemilattice can be embedded into 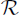 .
.
Theorem 1.2 (Sacks Splitting Theorem [1963b]). For every nonrecursive r.e. degreeathere are r.e. degreesb, c < asuch thatb ∨ c = a.
Theorem 1.3 (Sacks Density Theorem [1964]). For every pair of nonrecursive r.e. degreesa < bthere is an r.e. degreecsuch thata < c < b.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1996
References
REFERENCES
- 8
- Cited by

