Article contents
Optimal Proofs of Determinacy
Published online by Cambridge University Press: 15 January 2014
Extract
In this paper I shall present a method for proving determinacy from large cardinals which, in many cases, seems to yield optimal results. One of the main applications extends theorems of Martin, Steel and Woodin about determinacy within the projective hierarchy. The method can also be used to give a new proof of Woodin's theorem about determinacy in L(ℝ).
The reason we look for optimal determinacy proofs is not only vanity. Such proofs serve to tighten the connection between large cardinals and descriptive set theory, letting us bring our knowledge of one subject to bear on the other, and thus increasing our understanding of both. A classic example of this is the Harrington-Martin proof that 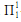 -determinacy implies
-determinacy implies 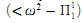 -determinacy. This is an example of a transfer theorem, which assumes a certain determinacy hypothesis and proves a stronger one. While the statement of the theorem makes no mention of large cardinals, its proof goes through 0#, first proving that
-determinacy. This is an example of a transfer theorem, which assumes a certain determinacy hypothesis and proves a stronger one. While the statement of the theorem makes no mention of large cardinals, its proof goes through 0#, first proving that
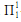 -determinacy ⇒ 0# exists,
-determinacy ⇒ 0# exists,
and then that
0# exists ⇒ 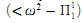 -determinacy
-determinacy
More recent examples of the connection between large cardinals and descriptive set theory include Steel's proof that
ADL(ℝ) ⇒ HODL(ℝ) ⊨ GCH,
see [9], and several results of Woodin about models of AD+, a strengthening of the axiom of determinacy AD which Woodin has introduced. These proofs not only use large cardinals, but also reveal a deep, structural connection between descriptive set theoretic notions and notions related to large cardinals.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1995
References
REFERENCES
- 29
- Cited by

