Article contents
Inner Models and Large Cardinals
Published online by Cambridge University Press: 15 January 2014
Extract
In this paper, we sketch the development of two important themes of modern set theory, both of which can be regarded as growing out of work of Kurt Gödel. We begin with a review of some basic concepts and conventions of set theory.
§0. The ordinal numbers were Georg Cantor's deepest contribution to mathematics. After the natural numbers 0, 1, …, n, … comes the first infinite ordinal number ω, followed by ω + 1, ω + 2, …, ω + ω, … and so forth. ω is the first limit ordinal as it is neither 0 nor a successor ordinal. We follow the von Neumann convention, according to which each ordinal number α is identified with the set {ν ∣ ν α} of its predecessors. The ∈ relation on ordinals thus coincides with <. We have 0 = ∅ and α + 1 = α ∪ {α}. According to the usual set-theoretic conventions, ω is identified with the first infinite cardinal ℵ0, similarly for the first uncountable ordinal number ω1 and the first uncountable cardinal number ℵ1, etc. We thus arrive at the following picture:
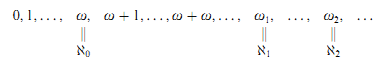
The von Neumann hierarchy divides the class V of all sets into a hierarchy of sets V α indexed by the ordinal numbers. The recursive definition reads: 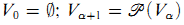 (where
(where 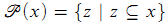 } is the power set of x);
} is the power set of x);
V λ = ∪v<λVv for limit ordinals λ. We can represent this hierarchy by the following picture.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1995
References
REFERENCES
- 31
- Cited by

