Article contents
Proper Forcing and Remarkable Cardinals
Published online by Cambridge University Press: 15 January 2014
Extract
The present paper investigates the power of proper forcings to change the shape of the universe, in a certain well-defined respect. It turns out that the ranking among large cardinals can be used as a measure for that power. However, in order to establish the final result I had to isolate a new large cardinal concept, which I dubbed “remarkability.” Let us approach the exact formulation of the problem—and of its solution—at a slow pace.
Breathtaking developments in the mid 1980s found one of its culminations in the theorem, due to Martin, Steel, and Woodin, that the existence of infinitely many Woodin cardinals with a measurable cardinal above them all implies that AD, the axiom of determinacy, holds in the least inner model containing all the reals, L(ℝ) (cf. [6[, p. 91). One of the nice things about AD is that the theory ZF + AD + V = L(ℝ) appears as a choiceless “completion” of ZF in that any interesting question (in particular, about sets of reals) seems to find an at least attractive answer in that theory (cf., for example, [5] Chap. 6). (Compare with ZF + V = L!) Beyond that, AD is very canonical as may be illustrated as follows.
Let us say that L(ℝ) is absolute for set-sized forcings if for all posets P ∈ V, for all formulae ϕ, and for all 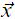 ∈ ℝ do we have that
∈ ℝ do we have that
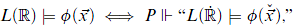
where  is a name for the set of reals in the extension.
is a name for the set of reals in the extension.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2000
References
REFERENCES
- 19
- Cited by

