Frege distinguished between an expression, its sense, and its reference, and he said that an expression expresses its sense and refers to, or denotes, its reference: bedeutet oder bezeichnet seine Bedeutung. But he was also very explicit that the passage from the expression to the reference goes via its sense, so what primarily refers is the sense, and then the expression comes to refer indirectly by composing these two arrows:

The purpose of this talk is to see how this sense/reference distinction comes out in the constructive meaning theory, or constructive semantics, that we now have, first of all for intuitionistic propositional and predicate logic, but also for more extensive systems, such as intuitionistic arithmetic and even stronger systems, and even for full intuitionistic type theory, of which both propositional and predicate logic and arithmetic are subsystems.
I am certainly not the first to address this question. The first person to do so is, as one would expect, Michael Dummett, in the mid-1970s, in two places. The first one was in a paper which was originally published in Spanish, “Frege’s Distinction Between Sense and Reference” [Reference Dummett1], although in Truth and Other Enigmas [Reference Dummett2] there is a slightly revised version of it, and then in The Logical Basis of Metaphysics [Reference Dummett3]. Although that appeared only in 1991, it is his William James Lectures from 1976, and I take it that the crucial passages with respect to this question were written in 1976, because they are almost verbatim the same as in the first reference. Then he addressed this question in a full lecture at Göran Sundholm’s invitation in 1992, and also at the invitation to talk exactly on this topic [Reference Dummett4].
What is now his basic idea? Let me quote from the first—well, I should say that also Moschovakis [Reference Moschovakis9] has addressed this issue, and the basic idea is the same. He indeed refers to Dummett, so it is enough if I quote from Dummett here.
In the first reference [Reference Dummett2, p. 133], Dummett says that
Frege’s argument about identity-statements would be met by supposing the sense of a singular term to be related to its reference as a programme to its execution
—I think it would be much better to say, as a programme to the result of its execution—
that is, if the sense provides an effective procedure of physical or mental operations, whereby the reference could be determined.
In the William James Lectures [Reference Dummett3, p. 125], he said that
sense will be related to semantic value as a programme to its execution,
so it is exactly the same idea.
I am in complete agreement with—well, I should quote, maybe, also from the third reference here, because the relation to Frege becomes completely clear there. In this paper [Reference Dummett4], Dummett says that
It is thus correct to regard numerical terms as aiming at natural numbers by varying routes, and hence to apply to each of them a distinction between its reference—the natural number aimed at—and its sense—the particular means for specifying that natural number.
Then he concludes by saying that
there is exactly the same reason for applying the sense/reference distinction to terms for natural numbers, and hence also expressions, simple or complex, for functions on the natural numbers, as there is in the classical case.
The next-to-last quotation is good for us, because there, Dummett actually uses exactly a formulation of Frege’s in his “Auseinandersetzung mit Biermann” [Reference Frege8, p. 95], which I take is on the threshold of the sense/reference distinction, though it is not yet there: he only has the distinction he had already in the Begriffsschrift [Reference Frege5], between expression and content, Zeichen und Inhalt. What Frege wrote there is that
verschiedene Zeichen für dieselbe Sache sind unvermeidlich, weil man auf verschiedenen Wegen auf sie hingeführt werden kann.
And then he takes the example, which is very close to Grundgesetze [Reference Frege7], of 4 as
![]() $2^2$
and as
$2^2$
and as
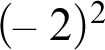 $(-2)^2$
, and says that
$(-2)^2$
, and says that
dies sind nur verschiedene Zeichen für dasselbe, deren Verschiedenheit nur die verschiedenen Wege andeutet, auf denen man diese selbe Sache erreichen kann.
So Dummett has clearly been directly inspired by these formulations of Frege’s when he spoke about the varying routes in the quotation that I gave to you.
I am in complete agreement with Dummett, and therefore also with Moschovakis, on the first point, namely what the sense/reference distinction amounts to for singular terms, or individual terms, as explained in these quotations. But I want to develop the theme more than that. In particular, I have something to say about what this distinction comes to for sentences.
Let me begin by displaying to you a mathematical object, and I will take a very simple one:
When I say that I am displaying an object to you, I mean that you should not think of what this refers to, but rather think of this itself that I display to you here, the object
![]() $2 + 2$
. From this object we can naturally obtain two other things.
$2 + 2$
. From this object we can naturally obtain two other things.
First of all, we can obtain the expression of the object, which looks the same, of course, the difference is that we change our attitude towards it. I use double quotation marks to indicate that change of attitude:
This is the expression of the object, and the relation between the object and the expression of the object goes in both directions here: From the object, we can pass to the expression by divesting the object of sense. Conversely, given the expression, since it is an expression that has been obtained from an object by disregarding its sense, we can also pass from it to the object by endowing it with sense again:

Of course, it is exactly this last step that is impossible if the expression here is not a well-formed one, a meaningful one, which is to say that it is not an expression which comes from an object, as it does in this particular case.
This mutual relation between an object and its expression has been particularly in the focus of Husserl’s interests, so I would like to mention Husserl’s terminology here. Husserl spoke of the step from the object to the expression as Sinnentleerung—divesting of sense, as I said—and of the opposite step as Sinnbelebung oder Sinnbeseelung, of course with a conscious use of a metaphor here, an interesting metaphor, namely that the expression is, so to say, the body of the object and the sense, the soul of the object.
On the other hand, we can calculate
![]() $2 + 2$
, and then the result depends on whether we think of it as a decimal number or a unary number. If we are dealing with decimal numbers, the result is, of course, 4, but I will throughout here think of numbers as unary numbers, which means that the result of the computation is—provided that I use
$2 + 2$
, and then the result depends on whether we think of it as a decimal number or a unary number. If we are dealing with decimal numbers, the result is, of course, 4, but I will throughout here think of numbers as unary numbers, which means that the result of the computation is—provided that I use
![]() ${\mathrm {s}}$
for the successor operation—so
${\mathrm {s}}$
for the successor operation—so
![]() $2 + 2$
evaluates to, or is calculated to,
$2 + 2$
evaluates to, or is calculated to,
![]() ${\mathrm {s}}({\mathrm {s}}({\mathrm {s}}({\mathrm {s}}(0))))$
in this canonical notation.
${\mathrm {s}}({\mathrm {s}}({\mathrm {s}}({\mathrm {s}}(0))))$
in this canonical notation.
Now we have already the semantic triangle with which I started up here:
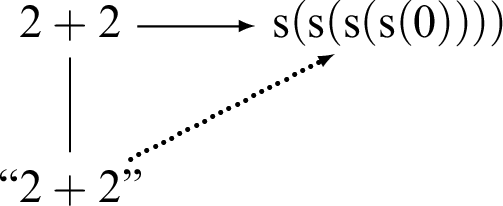
We have the expression, and we have the sense, and we have the reference. But I am drawing it consciously in this way, because we can perform the same change of attitude as I did over here with respect to the value, that is, to the reference,
![]() ${\mathrm {s}}({\mathrm {s}}({\mathrm {s}}({\mathrm {s}}(0))))$
. So, instead of looking at this number, I change the attitude and look upon it purely formally, which is then the corresponding numerical expression, “
${\mathrm {s}}({\mathrm {s}}({\mathrm {s}}({\mathrm {s}}(0))))$
. So, instead of looking at this number, I change the attitude and look upon it purely formally, which is then the corresponding numerical expression, “
![]() ${\mathrm {s}}({\mathrm {s}}({\mathrm {s}}({\mathrm {s}}(0))))$
.” We thus have the same mutual relation here as in the case of
${\mathrm {s}}({\mathrm {s}}({\mathrm {s}}({\mathrm {s}}(0))))$
.” We thus have the same mutual relation here as in the case of
![]() $2 + 2$
, and we also have an arrow going from the expression “
$2 + 2$
, and we also have an arrow going from the expression “
![]() $2 + 2$
” to the expression “
$2 + 2$
” to the expression “
![]() ${\mathrm {s}}({\mathrm {s}}({\mathrm {s}}({\mathrm {s}}(0))))$
,” namely the computation considered purely formally, as a sequence of mechanical steps, which is sheer symbol manipulation, where we forget completely about what the expressions mean. The semantic triangle is then in the upper left-hand corner here, and really only part of this, which you might call the semantic square:
${\mathrm {s}}({\mathrm {s}}({\mathrm {s}}({\mathrm {s}}(0))))$
,” namely the computation considered purely formally, as a sequence of mechanical steps, which is sheer symbol manipulation, where we forget completely about what the expressions mean. The semantic triangle is then in the upper left-hand corner here, and really only part of this, which you might call the semantic square:

I have explained this by means of a simple example, but the situation is quite general, so I could just as well have started with some arbitrary individual, that is, a member of an individual domain, let me call it a. We can divest it of sense and look upon the corresponding expression, “a” within quotes, and we have the mutual relation that I explained:

On the other hand, we can calculate a, unless a is already calculated, in which case it would have itself as result, as value, and I want to elaborate on how the passage from the object that we start with to its value proceeds in the language that I am concerned with here, namely type theory.
Let me go back for a moment to
![]() $2 + 2$
. How does the passage to
$2 + 2$
. How does the passage to
![]() ${\mathrm {s}}({\mathrm {s}}({\mathrm {s}}({\mathrm {s}}(0))))$
proceed? Well, you just follow the definitions of the symbols involved, which is to say that we have to see how 2 is defined, and 2 is defined as
${\mathrm {s}}({\mathrm {s}}({\mathrm {s}}({\mathrm {s}}(0))))$
proceed? Well, you just follow the definitions of the symbols involved, which is to say that we have to see how 2 is defined, and 2 is defined as
![]() ${\mathrm {s}}(1)$
, the successor of 1, so we must define 1, and 1 is defined as
${\mathrm {s}}(1)$
, the successor of 1, so we must define 1, and 1 is defined as
![]() ${\mathrm {s}}(0)$
, the successor of 0,
${\mathrm {s}}(0)$
, the successor of 0,
Then we must define addition, +, which is by the usual equations:
The passage from
![]() $2 + 2$
to
$2 + 2$
to
![]() ${\mathrm {s}}({\mathrm {s}}({\mathrm {s}}({\mathrm {s}}(0))))$
now proceeds via the following steps. We have
${\mathrm {s}}({\mathrm {s}}({\mathrm {s}}({\mathrm {s}}(0))))$
now proceeds via the following steps. We have
![]() $2 + 2$
, so we must see if the second argument is 0 or of successor form, hence we must replace it by its corresponding definiens, which is
$2 + 2$
, so we must see if the second argument is 0 or of successor form, hence we must replace it by its corresponding definiens, which is
![]() ${\mathrm {s}}(1)$
. Then we can apply rule (iv) to get
${\mathrm {s}}(1)$
. Then we can apply rule (iv) to get
![]() ${\mathrm {s}}(2 + 1)$
,
${\mathrm {s}}(2 + 1)$
,
Now we have already reached something whose outermost form is primitive, or canonical. I am going to use the terms “primitive” and “canonical” as synonymous, and “defined” and “non-canonical” as synonymous. What we have reached now is what is called in computer science the lazy value, or the value which is obtained by lazily evaluating
![]() $2+2$
, which means that we only compute it until we get its outermost primitive form.
$2+2$
, which means that we only compute it until we get its outermost primitive form.
But we can of course also continue to compute what is inside this canonical form, namely
![]() $2+1$
. Then we must see if the second argument is 0 or of successor form. Its definition is given by clause (ii), so we can apply (iv) again to get
$2+1$
. Then we must see if the second argument is 0 or of successor form. Its definition is given by clause (ii), so we can apply (iv) again to get
![]() ${\mathrm {s}}({\mathrm {s}}(2+0))$
, and now we use clause (iii) to get
${\mathrm {s}}({\mathrm {s}}(2+0))$
, and now we use clause (iii) to get
![]() ${\mathrm {s}}({\mathrm {s}}(2))$
, then clause (i) to get
${\mathrm {s}}({\mathrm {s}}(2))$
, then clause (i) to get
![]() ${\mathrm {s}}({\mathrm {s}}({\mathrm {s}}(1)))$
, and, finally, clause (ii) to get
${\mathrm {s}}({\mathrm {s}}({\mathrm {s}}(1)))$
, and, finally, clause (ii) to get
![]() ${\mathrm {s}}({\mathrm {s}}({\mathrm {s}}({\mathrm {s}}(0))))$
,
${\mathrm {s}}({\mathrm {s}}({\mathrm {s}}({\mathrm {s}}(0))))$
,
This is an example which shows the kind of computational mechanism that you have in arithmetic, and it is similar in type theory, where we have many more constructs.
From this example we can abstract the general situation, namely that if a is not already in primitive form, then it is defined, which is to say that it has the form of a definiendum, and then we can replace it by the corresponding definiens. Let me call a now
![]() $a_0$
. If
$a_0$
. If
![]() $a_0$
is defined, we replace it by its corresponding definiens,
$a_0$
is defined, we replace it by its corresponding definiens,
![]() $a_1$
, and then this may be primitive or defined. If it is defined, we replace it by its corresponding definiens, and so on until, eventually, we reach something which is of primitive form,
$a_1$
, and then this may be primitive or defined. If it is defined, we replace it by its corresponding definiens, and so on until, eventually, we reach something which is of primitive form,
![]() $a_n$
say, which is then what Curry very aptly called the ultimate definiens:
$a_n$
say, which is then what Curry very aptly called the ultimate definiens:
![]() $a_1$
is the immediate definiens, and
$a_1$
is the immediate definiens, and
![]() $a_n$
is the ultimate definiens, and that then is the result, or the value, of the computation,
$a_n$
is the ultimate definiens, and that then is the result, or the value, of the computation,
This fills in the first line in the semantic square in general, and of course we can then fill in the whole square. With respect to b here we can perform this change of attitude and consider instead the expression “b,” which is the same as the expression “
![]() $a_n$
,” and here we have the computation considered purely formally, as it is done, by the way, by a computer, which does not understand the senses of the symbols that it manipulates:
$a_n$
,” and here we have the computation considered purely formally, as it is done, by the way, by a computer, which does not understand the senses of the symbols that it manipulates:
This is the picture in the case of individual terms, or singular terms, and as I said, this is exactly how Dummett conceived of it. The difference comes when we go to the other base category, namely the category of propositions, or sentences and what they express, namely propositions.
I should say first of all here that the ground, or base, category that you have in type theory is, first of all, the category of propositions. To write that A and B are propositions, I am going to use the type-theoretical notation with a colon for the copula,
Given a proposition, A, we have the category of proofs of that proposition,
![]() ${\mathrm {prf}}(A)$
, and I will denote such proofs by small letters,
${\mathrm {prf}}(A)$
, and I will denote such proofs by small letters,
This covers also the previous example that I considered here, because propositions are identified in type theory, under the so-called Curry–Howard correspondence, with sets. (If you do not want to use the word “set,” say “individual domain” instead.) So, propositions are identified with sets, or individual domains, and in that case, instead of
![]() ${\mathrm {prf}}(A)$
, we have element of A, written
${\mathrm {prf}}(A)$
, we have element of A, written
![]() ${\mathrm {el}}(A)$
, or individual of the individual domain A:
${\mathrm {el}}(A)$
, or individual of the individual domain A:
The example that I considered previously was the example of an individual term, that is, a term of the category
![]() ${\mathrm {el}}(A)$
, but from this double interpretation under the Curry–Howard correspondence, you see that I have automatically also covered the case where a here is, not an element of an individual domain—for instance, a number, if A is the set of natural numbers—but I have also covered the case where a is an intuitionistic proof object. In that case, the computation that I have shown here is what is usually called, in proof-theoretical terminology, the process of normalization, for this is the passage from a to its normal form through the process of normalization.
${\mathrm {el}}(A)$
, but from this double interpretation under the Curry–Howard correspondence, you see that I have automatically also covered the case where a here is, not an element of an individual domain—for instance, a number, if A is the set of natural numbers—but I have also covered the case where a is an intuitionistic proof object. In that case, the computation that I have shown here is what is usually called, in proof-theoretical terminology, the process of normalization, for this is the passage from a to its normal form through the process of normalization.
I was on the point of beginning with the other ground category, or base category, and it is here that the difference with Dummett comes. The conclusion that Dummett reached in his lecture here 9 years ago concerning sentences was the following. He distinguished, first, between predicates, relational expressions, and logical constants, on the one hand, and we should include sentences there also, and on the other hand, the singular terms and the functional expressions, that is, open terms, if it is in first-order arithmetic or first-order logic. So these two kinds. Then he said that, for expressions of the former kind, that is, which includes sentences, there is no room for a distinction analogous to that between sense and reference, and then he concludes the argument by saying that, alas, for sentences constructively understood there can be no distinction between sense and reference.
It is very clear why he said this, namely that constructively—if you take this picture and replace the individual a here by a proposition instead, A say, then there is no—then it is as easy to make the step from A to “A” as it was before, but we know that, for Frege, the reference of a sentence was a truth value, and it is impossible—it was known at Frege’s time as well as it is now after the 1930s that it is impossible to calculate the truth value, in general, of a proposition. It is impossible to try to complete this picture, as we would have to do if we were entirely faithful to Frege, that is, to end up here with something that is either the True or the False. This is not possible. Had it been possible, then the logical positivist attempt of explaining what a proposition is by saying that it is a method of verification—I mean, the verificationism of the 1930s—would have been all right, if the passage from a sentence to its truth value had been effective and could have been achieved by a sequence of computational steps. As we know, this is not possible, and hence it was very natural for Dummett to say that there is no analogue of the sense/reference distinction for sentences.
Now, I do not think that this is the correct conclusion to draw, because even propositions can be primitive and defined. The primitive propositions are those whose meanings we explain classically by directly giving the truth condition for the proposition in question, or intuitionistically by explaining what a canonical proof of the proposition looks like. So those are the primitive propositions, and typically, conjunction, implication, universal quantification, etc. give primitive propositions in this sense, because their meaning is explained in precisely this way. But there are other propositions whose meanings we do not explain directly by laying down the truth, or intuitionistically, the proof condition for them, but whose meanings we explain by means of a nominal definition. The most typical example is negation. In intuitionistic logic, the negation of A,
![]() $\neg A$
, is defined as
$\neg A$
, is defined as
and material equivalence,
![]() $A\Leftrightarrow B$
, is defined as
$A\Leftrightarrow B$
, is defined as
These are exceedingly simple definitions, but already they give rise to one computational step, namely from
![]() $\neg A$
to
$\neg A$
to
![]() $A\supset \bot $
and from
$A\supset \bot $
and from
![]() $A\Leftrightarrow B$
to
$A\Leftrightarrow B$
to
![]() $(A \supset B) \wedge (B \supset A)$
. So we get chains of length one up here. That is already in propositional logic.
$(A \supset B) \wedge (B \supset A)$
. So we get chains of length one up here. That is already in propositional logic.
If you go to more powerful languages such as—arithmetic is not good enough, as an example I need to go to a language such as type theory, where you have the possibility of having a formalized Tarskian truth definition or something which is very similar to it, namely what I call universes in type theory, but since I take that as less well known, let me stick with the formalized Tarskian truth definition.
In formalizing that in type theory, you will introduce a set, or a domain, of formulas,
![]() ${\mathrm {form}}$
, and the formulas are defined by the usual inductive definition. So you will have a base clause such as
${\mathrm {form}}$
, and the formulas are defined by the usual inductive definition. So you will have a base clause such as
saying that
![]() ${\mathrm {abs}}$
is a formula, an element of the set of formulas. It is the code, or the descriptive name, of absurdity,
${\mathrm {abs}}$
is a formula, an element of the set of formulas. It is the code, or the descriptive name, of absurdity,
![]() $\bot $
. And we will have a unary operation that takes an arbitrary formula, a say, to the code of the negation of a:
$\bot $
. And we will have a unary operation that takes an arbitrary formula, a say, to the code of the negation of a:

I am imitating Tarski’s own way of writing these descriptive names.
Let me take one example, maybe the proposition
![]() $\neg \neg \bot $
. It has, in this notation, the structure of the descriptive name
$\neg \neg \bot $
. It has, in this notation, the structure of the descriptive name
![]() ${\mathrm {neg}}^\frown {\mathrm {neg}}^\frown {\mathrm {abs}}$
.
${\mathrm {neg}}^\frown {\mathrm {neg}}^\frown {\mathrm {abs}}$
.
These are two of the clauses generating the set of formulas, and we have other clauses for the other logical operations. Then there will be the formalization of Tarski’s truth definition. For any formula a, we will have a proposition
![]() ${\mathrm {T}}(a)$
:
${\mathrm {T}}(a)$
:

The truth predicate is defined by the usual clauses, of which two are as follows:
 $$ \begin{align*} {\mathrm{T}}({\mathrm{abs}}) & = \bot : {\mathrm{prop}}, \\ {\mathrm{T}}({\mathrm{neg}}^\frown a) &= \neg{\mathrm{T}}(a) : {\mathrm{prop}}. \end{align*} $$
$$ \begin{align*} {\mathrm{T}}({\mathrm{abs}}) & = \bot : {\mathrm{prop}}, \\ {\mathrm{T}}({\mathrm{neg}}^\frown a) &= \neg{\mathrm{T}}(a) : {\mathrm{prop}}. \end{align*} $$
As soon as we have such a formalized truth definition, then there is no problem in defining, by recursion, some astronomically big formula. We could define a function, say
![]() $f(n)$
, which takes formulas as values, and n is a number, and we do it by the following recursion:
$f(n)$
, which takes formulas as values, and n is a number, and we do it by the following recursion:
 $$ \begin{align*} f(0) & = {\mathrm{abs}}, \\ f({\mathrm{s}}(n)) & = {\mathrm{neg}}^\frown f(n). \end{align*} $$
$$ \begin{align*} f(0) & = {\mathrm{abs}}, \\ f({\mathrm{s}}(n)) & = {\mathrm{neg}}^\frown f(n). \end{align*} $$
Then we can apply f to some astronomically big number and get f of, say,
![]() $10^{10^{10}}$
. It will be a formula,
$10^{10^{10}}$
. It will be a formula,
 $$ \begin{align*} f(10^{10^{10}}) : {\mathrm{form}}, \end{align*} $$
$$ \begin{align*} f(10^{10^{10}}) : {\mathrm{form}}, \end{align*} $$
hence we can apply the truth predicate and get
 $$ \begin{align*} {\mathrm{T}}(f(10^{10^{10}})) : {\mathrm{prop}}. \end{align*} $$
$$ \begin{align*} {\mathrm{T}}(f(10^{10^{10}})) : {\mathrm{prop}}. \end{align*} $$
Now I have constructed a proposition that could serve as my A here, where the number of computation steps to reduce it to full normal form, that is, to compute it fully, is of the order of magnitude
![]() $10^{10^{10}}$
, because the normal form of this proposition is
$10^{10^{10}}$
, because the normal form of this proposition is
with
![]() $10^{10^{10}}$
negation signs in front, which means that the reference—or I should not say reference yet—the value of this proposition, if we compute it, is something that we—it is not feasible for us to confront ourselves with it, and we will never get to see this in full. We have access to this proposition, this canonical proposition, only as the result of evaluating the proposition
$10^{10^{10}}$
negation signs in front, which means that the reference—or I should not say reference yet—the value of this proposition, if we compute it, is something that we—it is not feasible for us to confront ourselves with it, and we will never get to see this in full. We have access to this proposition, this canonical proposition, only as the result of evaluating the proposition
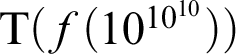 ${\mathrm {T}}(f(10^{10^{10}}))$
, which we do have access to.
${\mathrm {T}}(f(10^{10^{10}}))$
, which we do have access to.
It is clear that the picture now is the same in a certain respect as for individual terms, namely that also propositions can be primitive and defined, and if they are defined, they can be calculated. The only difference with the classical case is that we cannot calculate them to a truth value, but we can calculate them to canonical form. It is this canonical form which in constructive semantics replaces the Fregean truth value. I take it that Thomas Ricketts’ students will react with a sigh of relief at this point, that there is no need any longer to contort our minds into believing that it is the True or the False, these two objects, which are the only possible references of sentences.Footnote 1 What are references of sentences are canonical propositions. So, truth values are replaced by canonical propositions.
I have now dealt with the two base categories, propositions and individuals, and at the same time proof objects, and let me now go to the higher categories, the function categories.
We know that the question of the reference of incomplete expressions is something which has been discussed at length. It is a contestable point in Fregean interpretation, and Dummett devotes a whole long, 40-page chapter to it in his Frege book. It does not matter now whether by functional expression I mean an expression of a function in the old-fashioned sense—by which I mean a function of variables—or if I take a function in the modern sense—which is not a function of a variable, but which receives its argument by application—because the remarks about the sense/reference distinction are the same in both cases. In the former case, we could think of something like
 $$ \begin{align*} x^2+3y, \end{align*} $$
$$ \begin{align*} x^2+3y, \end{align*} $$
and in the latter case something like the factorial function,
If you ask, in cases like these, What is its reference, its value?, then you immediately get a counter-question: I cannot give you the value of
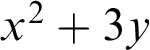 $x^2+3y$
unless you tell me for what arguments you want it. And similarly in this case: I cannot give you the value of the factorial function—if you tell me what you want the factorial of, I can give you the result: if you want it for 5, for instance, it is 120.
$x^2+3y$
unless you tell me for what arguments you want it. And similarly in this case: I cannot give you the value of the factorial function—if you tell me what you want the factorial of, I can give you the result: if you want it for 5, for instance, it is 120.
I think this first impression here is entirely correct, that there is no value, or reference, for a functional expression in the sense that you ask me for the value, and I give you something back. I can only give you something back for certain arguments. I certainly read Frege in this way as well, for when Frege discusses, in §29 of Grundgesetze, the reference of functional expressions, he is not explaining what the reference is: he is explaining what it means for a functional expression to have a reference, or to refer to something, or to be referential. That is what he explains: hat eine Bedeutung, bedeutet etwas, ist bedeutungsvoll. That is what he is defining. I would not—there is no reason to have any quarrel about saying that these are referential expressions. But what does it mean for them to be referential? Well, that means precisely that they refer in the proper sense that I have already explained, provided that we complete them by referring expressions. So I think that, on this point, there is agreement with Frege, at least with how I read this particular place in the Grundgesetze. Maybe there are other places that I am not aware of.
So the conclusion here is that, of the picture of the semantic square that I showed you for the two ground categories, of that picture there remains only the left part. Namely, if we have a function in the old-fashioned sense, we can certainly divest it of sense and look at the functional expression, and vice versa, and if it is a function in the modern sense, such as
![]() ${\mathrm {fac}}$
here, then we can do the same:
${\mathrm {fac}}$
here, then we can do the same:

But there is no way of passing to any value here, unless you first saturate the function by providing it with arguments. So this is—for functional expressions, that is, expressions of the higher types—different from what it is at the ground types.
The last part of my talk will be devoted to the question of what equalities are involved in relation to the semantic triangle. We have expression, sense, and reference. What are the identity criteria that we have for expressions, senses, and references?
Let me begin with expressions. First of all, we have the, so to say, trivial equality relation of syntactical identity, where two expressions are syntactically identical if they have identical forms, that is, graphically the same form and identical parts, and then you go down to the bottom of the expression.
This is maximally strict equality, but it seems to me that a closely related equality is more important, where you allow notational variants, that is, so to say, the equivalence relation which is generated by the principle of the arbitrariness of the sign, in Saussure’s terminology, l’arbitraire du signe. So we do not care about the particular graphical shape that we are using. We may have different shapes, as, say, for conjunction we may have the ampersand, &, and we have the sign
![]() $\wedge $
. For the factorial function you have not only the modern notation
$\wedge $
. For the factorial function you have not only the modern notation
![]() ${\mathrm {fac}}$
, you have also the old-fashioned notation
${\mathrm {fac}}$
, you have also the old-fashioned notation
![]() $!$
. And you have ordinary abbreviations—I do not mean what we logicians call abbreviations, but ordinary abbreviations, such as “etc.” You have graphical differences, but the meaning is the same.
$!$
. And you have ordinary abbreviations—I do not mean what we logicians call abbreviations, but ordinary abbreviations, such as “etc.” You have graphical differences, but the meaning is the same.
Once we have set up such a dictionary of alternative notations, that will immediately determine an equivalence relation between expressions, which I will denote by three bars,
![]() $\equiv $
, and which I think is the appropriate relation to identify as the synonymy relation. This is a relation between expressions: two expressions stand in this relation to each other if their forms are synonymous according to the lexicon that you have, and their corresponding parts are also synonymous, and this includes in particular renaming of bound variables. It is clear that different names for bound variables have this character. This is the relation that I will call synonymy, and as you see, this is very close to Carnap’s notion of intensional isomorphism. The only difference is that, in the bottom, that is, for the atomic parts, Carnap required them to be logically equivalent, L-equivalent, whereas what he said about—that the expression should have the same structure—is entirely the same as what I am saying here. So I am replacing the notion of L-equivalence for the atomic parts by the relation of notational variance as given by the lexicon.
$\equiv $
, and which I think is the appropriate relation to identify as the synonymy relation. This is a relation between expressions: two expressions stand in this relation to each other if their forms are synonymous according to the lexicon that you have, and their corresponding parts are also synonymous, and this includes in particular renaming of bound variables. It is clear that different names for bound variables have this character. This is the relation that I will call synonymy, and as you see, this is very close to Carnap’s notion of intensional isomorphism. The only difference is that, in the bottom, that is, for the atomic parts, Carnap required them to be logically equivalent, L-equivalent, whereas what he said about—that the expression should have the same structure—is entirely the same as what I am saying here. So I am replacing the notion of L-equivalence for the atomic parts by the relation of notational variance as given by the lexicon.
If we now pass from expressions to sense, we have a novelty of type theory. We have the relation of intensional equality, which in type theory is written like this:
To explain this form of judgement, I will make use of the scholastic notion of supposition, that is, the notion of what an expression stands for on a particular occasion of use. Corresponding to the three vertices in the semantic triangle, which I gave at the beginning of this lecture, we may distinguish between those cases where an expression stands for itself, those where it stands for its meaning, and those where it stands for its reference. I indicate supposition of the first kind with double quotes, supposition of the second kind, or meaning supposition, with single quotes—I need to have different kinds of quotes anyway—and for referential supposition, when we are talking about things, as we are normally doing, I will not use any special indication.
Now we may ask, What supposition do we have in the type-theoretical forms of judgement? It can be seen that, in the fundamental form of judgement,
![]() $a:A$
, we have referential supposition to the right of the copula and meaning supposition to the left of the copula. This applies also to the equality judgement,
$a:A$
, we have referential supposition to the right of the copula and meaning supposition to the left of the copula. This applies also to the equality judgement,
![]() $a=b:A$
, where we have meaning supposition on the left-hand side. The proper way of reading the intensional, or definitional, equality judgement (Int-id) is therefore that, in Frege’s terminology, the senses ‘a’ and ‘b’ are co-referential. So, whereas
$a=b:A$
, where we have meaning supposition on the left-hand side. The proper way of reading the intensional, or definitional, equality judgement (Int-id) is therefore that, in Frege’s terminology, the senses ‘a’ and ‘b’ are co-referential. So, whereas
![]() $a\equiv b$
is the relation of synonymy, that is, Sinnesgleichheit, intensional equality is the relation of Bedeutungsgleichheit.
$a\equiv b$
is the relation of synonymy, that is, Sinnesgleichheit, intensional equality is the relation of Bedeutungsgleichheit.
Then, finally, we have the identity we are used to, namely the identity relation that we have in predicate logic. This is the identity relation that Frege had both in the Begriffsschrift and in the Grundgesetze and which is expressed by a binary propositional function subject to the reflexivity law and Leibniz’s Law. In type theory you will have that identity relation, say
![]() ${\mathrm {Id}}(A, a, b)$
, on each individual domain A. Given such an identity proposition, we can form the judgement in which that proposition is held true,
${\mathrm {Id}}(A, a, b)$
, on each individual domain A. Given such an identity proposition, we can form the judgement in which that proposition is held true,
Because of what I said here about the difference in supposition between the left-hand side and the right-hand side, and because of the interpretation of a judgement of the form
—constructively, and especially in type theory, this is regarded as an abbreviated way of saying that you have a proof of A, you are just not showing the proof explicitly, I am simply suppressing the proof—since the right-hand side here is referentially transparent, that means that when I am suppressing the proof in
![]() $a:A$
, I am suppressing precisely the part of the complete judgement that is not transparent, the intensional part of the judgement, and what remains is the judgement
$a:A$
, I am suppressing precisely the part of the complete judgement that is not transparent, the intensional part of the judgement, and what remains is the judgement
![]() $A{\;\mathrm {true}}$
, where now A is referentially transparent.
$A{\;\mathrm {true}}$
, where now A is referentially transparent.
In particular, the identity proposition in the judgement (Ext-id) ends up in a referentially transparent position, which means that the appropriate way of reading this judgement is that a and b are the same, that is, the references of ‘a’ and ‘b’ are the same.
And observe the—subtle, maybe, when you see it the first time—difference between (Int-id) and (Ext-id). The judgement
![]() $a=b:A$
says of the two senses ‘a’ and ‘b’ that they are co-referential, whereas the judgement
$a=b:A$
says of the two senses ‘a’ and ‘b’ that they are co-referential, whereas the judgement
![]() ${\mathrm {Id}}(A, a, b){\;\mathrm {true}}$
says something about their references, which is to say, about a and b.
${\mathrm {Id}}(A, a, b){\;\mathrm {true}}$
says something about their references, which is to say, about a and b.
It is precisely this difficulty that Frege was grappling with in his discussion about identity, in the Begriffsschrift first and then on the beginning page of “Über Sinn und Bedeutung” [Reference Frege6]. He corrected himself, essentially from having thought that identity was something like (Int-id) to saying, No, identity is in fact a relation between objects, and not between linguistic entities. And that effect, so to say, that an identity proposition—or rather, an identity judgement—is about the objects, and neither about the linguistic expressions thought of as identical expressions, nor about their meanings, that effect comes about because of the referential transparency of the position into which the identity proposition is put in (Ext-id).


