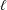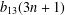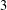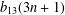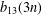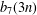Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Adiga, Chandrashekar
and
Dasappa, Ranganatha
2018.
Congruences for 7 and 49-regular partitions modulo powers of 7.
The Ramanujan Journal,
Vol. 46,
Issue. 3,
p.
821.
Penniston, David
2019.
11-Regular partitions and a Hecke eigenform.
International Journal of Number Theory,
Vol. 15,
Issue. 06,
p.
1251.
Chern, Shane
Tang, Dazhao
and
Xia, Ernest X. W.
2020.
Arithmetic properties for 7-regular partition triples.
Indian Journal of Pure and Applied Mathematics,
Vol. 51,
Issue. 2,
p.
717.
DA SILVA, ROBSON
and
SELLERS, JAMES A.
2021.
ARITHMETIC PROPERTIES OF 3-REGULAR PARTITIONS IN THREE COLOURS.
Bulletin of the Australian Mathematical Society,
Vol. 104,
Issue. 3,
p.
415.
PENNISTON, DAVID
2023.
-REGULAR PARTITIONS AND MODULAR FORMS WITH COMPLEX MULTIPLICATION.
Bulletin of the Australian Mathematical Society,
Vol. 108,
Issue. 2,
p.
254.
Murugan, P.
and
Fathima, S. N.
2023.
Arithmetic properties of 3-regular 6-tuple partitions.
Indian Journal of Pure and Applied Mathematics,
Vol. 54,
Issue. 4,
p.
1249.
El-Guindy, Ahmad
and
Ghazy, Mostafa M.
2024.
$$\ell $$-Adic properties and congruences of $$\ell $$-regular partition functions.
Research in Number Theory,
Vol. 10,
Issue. 4,