Hostname: page-component-7f64f4797f-7vqc4 Total loading time: 0 Render date: 2025-11-06T10:46:39.692Z Has data issue: false hasContentIssue false
  • English
  • Français

CANONICAL DECOMPOSITION AND QUIVER REPRESENTATIONS OF TYPE 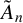$\tilde {A}_n$ OVER FINITE FIELDS

Part of: Representation theory of rings and algebras

Published online by Cambridge University Press:  22 September 2022

QINGHUA CHEN Open the ORCID record for QINGHUA CHEN [Opens in a new window]  and
YE LIU Open the ORCID record for YE LIU [Opens in a new window]
QINGHUA CHEN*
Affiliation:
School of Mathematics and Statistics, Fu Zhou University, Fu Zhou, Fujian 350108, PR China
YE LIU
Affiliation:
School of Mathematical Sciences, Beijing Normal University, Beijing 100875, PR China Current address: The high school attached to Hunan Normal University, Chang Sha, Hunan 410006, PR China e-mail: 252241859@qq.com
*
e-mail: 252241859@qq.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let Q be a quiver of type 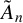$\tilde {A}_n$. Let 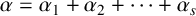$\alpha =\alpha _1+\alpha _2+\cdots +\alpha _s$ be the canonical decomposition. For the polynomials 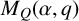$M_Q(\alpha ,q)$ that count the number of isoclasses of representations of Q over 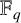${\mathbb F}_q$ with dimension vector 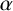$\alpha $, we obtain a precise relation between the degree of 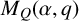$M_Q(\alpha ,q)$ and that of 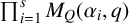$\prod _{i=1}^{s} M_Q(\alpha _i,q)$ for an arbitrary dimension vector 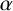$\alpha $.

Keywords

canonical decompositionquiver representationdimension vector

MSC classification

Primary: 16G20: Representations of quivers and partially ordered sets

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 107 , Issue 2 , April 2023 , pp. 250 - 260
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Auslander, M., Reiten, I. and Smalø, S., Representation Theory of Artin Algebras, Cambridge Studies in Advanced Mathematics, 36 (Cambridge University Press, Cambridge, 1997).Google Scholar
Chen, Q. and Liu, Y., ‘Canonical decomposition and quiver representations over finite field’, Comm. Algebra 46(11) (2018), 4859–4867.CrossRefGoogle Scholar
Crawley-Boevey, W. W. and Van den Bergh, M., ‘Absolutely indecomposable representations and Kac–Moody Lie algebras’, Invent. Math. 155(3) (2001), 537–559, with an appendix by H. Nakajima.Google Scholar
Deng, B., Du, J., Parshall, B. and Wang, J., Finite Dimensional Algebras and Quantum Groups, Mathematical Surveys and Monographs, 150 (American Mathematical Society, Providence, RI, 2008).CrossRefGoogle Scholar
Derksen, H. and Weyman, J., ‘On the canonical decomposition of quiver representations’, Compos. Math. 133 (2002), 245–265.CrossRefGoogle Scholar
Dlab, V. and Ringel, C. M., Indecomposable Representations of Graphs and Algebras, Memoirs of the American Mathematical Society, 6(173) (American Mathematical Society, Providence, RI, 1976).CrossRefGoogle Scholar
Gabriel, P., ‘Unzerlegbare Darstellungen I’, Manuscripta Math. 6 (1972), 71–103.CrossRefGoogle Scholar
Hua, J., ‘Counting representations of quivers over finite fields’, J. Algebra 226 (2000), 1011–1013.CrossRefGoogle Scholar
Kac, V., ‘Infinite root systems, representations of graphs and invariant theory’, Invent. Math. 56 (1980), 57–92.CrossRefGoogle Scholar
Kac, V., ‘Infinite root systems, representations of graphs and invariant theory II’, J. Algebra 78 (1982), 141–162.CrossRefGoogle Scholar
Schofield, A., ‘General representations of quivers’, Proc. Lond. Math. Soc. (3) 65 (1992), 46–64.CrossRefGoogle Scholar