Article contents
EQUIVALENCE OF SEMI-NORMS RELATED TO SUPER WEAKLY COMPACT OPERATORS
Published online by Cambridge University Press: 22 June 2021
Abstract
We study super weakly compact operators through a quantitative method. We introduce a semi-norm 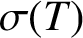 $\sigma (T)$ of an operator
$\sigma (T)$ of an operator 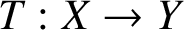 $T:X\to Y$, where X, Y are Banach spaces, the so-called measure of super weak noncompactness, which measures how far T is from the family of super weakly compact operators. We study the equivalence of the measure
$T:X\to Y$, where X, Y are Banach spaces, the so-called measure of super weak noncompactness, which measures how far T is from the family of super weakly compact operators. We study the equivalence of the measure 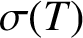 $\sigma (T)$ and the super weak essential norm of T. We prove that Y has the super weakly compact approximation property if and and only if these two semi-norms are equivalent. As an application, we construct an example to show that the measures of T and its dual
$\sigma (T)$ and the super weak essential norm of T. We prove that Y has the super weakly compact approximation property if and and only if these two semi-norms are equivalent. As an application, we construct an example to show that the measures of T and its dual 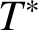 $T^*$ are not always equivalent. In addition we give some sequence spaces as examples of Banach spaces having the super weakly compact approximation property.
$T^*$ are not always equivalent. In addition we give some sequence spaces as examples of Banach spaces having the super weakly compact approximation property.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 104 , Issue 3 , December 2021 , pp. 506 - 518
- Copyright
- © 2021 Australian Mathematical Publishing Association Inc.
Footnotes
Supported in part by NSFC, grant no. 11701501, and funding from Yangzhou University.
References
- 2
- Cited by


