Published online by Cambridge University Press: 22 November 2019
A Ducci sequence is a sequence of integer  $n$-tuples obtained by iterating the map Such a sequence is eventually periodic and we denote by
$n$-tuples obtained by iterating the map Such a sequence is eventually periodic and we denote by 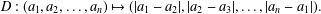 $$\begin{eqnarray}D:(a_{1},a_{2},\ldots ,a_{n})\mapsto (|a_{1}-a_{2}|,|a_{2}-a_{3}|,\ldots ,|a_{n}-a_{1}|).\end{eqnarray}$$
$$\begin{eqnarray}D:(a_{1},a_{2},\ldots ,a_{n})\mapsto (|a_{1}-a_{2}|,|a_{2}-a_{3}|,\ldots ,|a_{n}-a_{1}|).\end{eqnarray}$$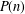 $P(n)$ the maximal period of such sequences for given odd
$P(n)$ the maximal period of such sequences for given odd  $n$. We prove a lower bound for
$n$. We prove a lower bound for 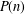 $P(n)$ by counting certain partitions. We then estimate the size of these partitions via the multiplicative order of two modulo
$P(n)$ by counting certain partitions. We then estimate the size of these partitions via the multiplicative order of two modulo  $n$.
$n$.
The second author was supported in part by the Australian Research Council Grant DP180100201.