No CrossRef data available.
Article contents
ON THE REGULAR GRAPH RELATED TO THE G-CONJUGACY CLASSES
Published online by Cambridge University Press: 12 May 2021
Abstract
Given a finite group G with a normal subgroup N, the simple graph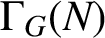 
$\Gamma _{\textit {G}}( \textit {N} )$ is a graph whose vertices are of the form 
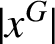$|x^G|$, where 
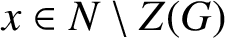$x\in {N\setminus {Z(G)}}$ and 
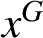$x^G$ is the G-conjugacy class of N containing the element x. Two vertices 
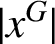$|x^G|$ and 
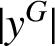$|y^G|$ are adjacent if they are not coprime. We prove that, if 
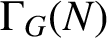$\Gamma _G(N)$ is a connected incomplete regular graph, then 
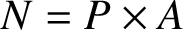$N= P \times {A}$ where P is a p-group, for some prime p, 
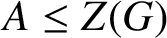$A\leq {Z(G)}$ and 
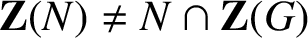$\textbf {Z}(N)\not = N\cap \textbf {Z}(G)$.
MSC classification
Primary:
20E45: Conjugacy classes
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 105 , Issue 1 , February 2022 , pp. 101 - 105
- Copyright
- © 2021 Australian Mathematical Publishing Association Inc.
Footnotes
The research of the second author was in part supported by a grant from IPM (No. 1400200028).
References
Beltrán, A., Felipe, M. J. and Melchor, C., ‘Graphs associated to conjugacy classes of normal subgroups in finite groups’,
J. Algebra
443 (2015), 335–348.CrossRefGoogle Scholar
Bertram, E. A., Herzog, M. and Mann, A., ‘On a graph related to conjugacy classes of groups’,
Bull. Lond. Math. Soc.
22(6) (1990), 569–575.CrossRefGoogle Scholar
Bianchi, M., Camina, R. D., Herzog, M. and Pacifici, E., ‘Conjugacy classes of finite groups and graph regularity’,
Forum Math.
27(6) (2015), 3167–3172.CrossRefGoogle Scholar
Bianchi, M., Herzog, M., Pacifici, E. and Saffirio, G., ‘On the regularity of a graph related to conjugacy classes of groups’,
European J. Combin.
33(7) (2012), 1402–1407.CrossRefGoogle Scholar
Camina, A. R. and Camina, R. D., ‘The influence of conjugacy class sizes on the structure of finite groups: a survey’,
Asian-Eur. J. Math.
4(4) (2011), 559–588.CrossRefGoogle Scholar
Lewis, M. L., ‘An overview of graphs associated with character degrees and conjugacy class sizes in finite groups’,
Rocky Mountain J. Math.
38 (2008), 175–211.CrossRefGoogle Scholar