Hostname: page-component-7dd5485656-hw7sx Total loading time: 0 Render date: 2025-10-31T14:57:47.061Z Has data issue: false hasContentIssue false
  • English
  • Français

SUMSETS CONTAINING A TERM OF A SEQUENCE

Part of: Sequences and sets

Published online by Cambridge University Press:  18 September 2023

MIN CHEN Open the ORCID record for MIN CHEN [Opens in a new window]  and
MIN TANG Open the ORCID record for MIN TANG [Opens in a new window]
MIN CHEN
Affiliation:
School of Mathematics and Statistics, Anhui Normal University, Wuhu 241002, PR China e-mail: 2395409935@qq.com
MIN TANG*
Affiliation:
School of Mathematics and Statistics, Anhui Normal University, Wuhu 241002, PR China
*
e-mail: tmzzz2000@163.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 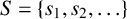$S=\{s_{1}, s_{2}, \ldots \}$ be an unbounded sequence of positive integers with 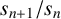$s_{n+1}/s_{n}$ approaching 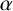$\alpha $ as 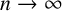$n\rightarrow \infty $ and let 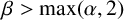$\beta>\max (\alpha , 2)$. We show that for all sufficiently large positive integers l, if 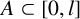$A\subset [0, l]$ with 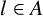$l\in A$, 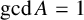$\gcd A=1$ and 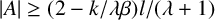$|A|\geq (2-{k}/{\lambda \beta })l/(\lambda +1)$, where 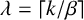$\lambda =\lceil {k}/{\beta }\rceil $, then 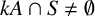$kA\cap S\neq \emptyset $ for 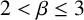$2<\beta \leq 3$ and 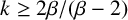$k\geq {2\beta }/{(\beta -2)}$ or for 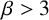$\beta>3$ and 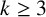$k\geq 3$.

Keywords

sumsetssequencespowers of an integer

MSC classification

Primary: 11B13: Additive bases, including sumsets

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 109 , Issue 3 , June 2024 , pp. 420 - 428
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This work was supported by the National Natural Science Foundation of China (Grant Nos. 11071033, 12371003) and the Top Talents Project of Anhui Department of Education (Grant No. gxbjZD05).

References

Abe, T., ‘Sumsets containing powers of an integer’, Combinatorica 24 (2004), 1–4.CrossRefGoogle Scholar
Erdős, P. and Freiman, G., ‘On two additive problems’, J. Number Theory 34 (1990), 1–12.CrossRefGoogle Scholar
Kapoor, V., ‘Set whose sumset avoids a thin sequence’, J. Number Theory 130 (2010), 534–538.CrossRefGoogle Scholar
Lev, V. F., ‘Representing powers of 2 by a sum of four integers’, Combinatorica 16 (1996), 413–416.CrossRefGoogle Scholar
Lev, V. F., ‘Structure theorem for multiple addition and the Frobenius problem’, J. Number Theory 58 (1996), 79–78.CrossRefGoogle Scholar
Nathanson, M. B. and Sárközy, A., ‘Sumsets containing long arithmetic progressions and powers of 2’, Acta Arith. 54 (1989), 147–154.CrossRefGoogle Scholar
Pan, H., ‘Note on integer powers in sumsets’, J. Number Theory 117 (2006), 216–221.CrossRefGoogle Scholar
Wu, X. and Chen, Y. Q., ‘Note on powers of 2 in sumsets’, Appl. Math. Lett. 25 (2012), 932–936.CrossRefGoogle Scholar