No CrossRef data available.
Article contents
A BIJECTION OF INVARIANT MEANS ON AN AMENABLE GROUP WITH THOSE ON A LATTICE SUBGROUP
Published online by Cambridge University Press: 18 January 2021
Abstract
Suppose G is an amenable locally compact group with lattice subgroup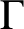 
$\Gamma $. Grosvenor [‘A relation between invariant means on Lie groups and invariant means on their discrete subgroups’, Trans. Amer. Math. Soc. 288(2) (1985), 813–825] showed that there is a natural affine injection 
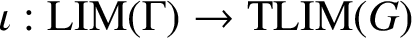$\iota : {\text {LIM}}(\Gamma )\to {\text {TLIM}}(G)$ and that 
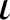$\iota $ is a surjection essentially in the case 
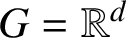$G={\mathbb R}^d$, 
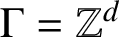$\Gamma ={\mathbb Z}^d$. In the present paper it is shown that 
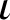$\iota $ is a surjection if and only if 
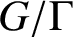$G/\Gamma $ is compact.
MSC classification
Secondary:
22F30: Homogeneous spaces
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 104 , Issue 2 , October 2021 , pp. 302 - 307
- Copyright
- © 2021 Australian Mathematical Publishing Association Inc.
References
Bader, U., Caprace, P.-E., Gelander, T. and Mozes, S., ‘Lattices in amenable groups’, Fundamenta Math. 246(3) (2019), 217–255.CrossRefGoogle Scholar
Greenleaf, F. P., Invariant Means on Topological Groups and Their Applications (Van Nostrand, New York, 1969).Google Scholar
Grosvenor, J. R., ‘A relation between invariant means on Lie groups and invariant means on their discrete subgroups’, Trans. Amer. Math. Soc. 288(2) (1985), 813–825.CrossRefGoogle Scholar
Hopfensperger, J., ‘When is an invariant mean the limit of a Følner net?’, Preprint, 2020, arXiv:2003.00251 [math.FA].CrossRefGoogle Scholar
Paterson, A. L. T., Amenability (American Mathematical Society, Providence, RI, 1988).CrossRefGoogle Scholar
Raughunathan, M. S., Discrete Subgroups of Lie Groups (Springer-Verlag, Berlin, 1972).CrossRefGoogle Scholar
Weil, A., L’Intégration dans les Groupes Topologiques et ses Applications (Hermann, Paris, 1953).Google Scholar