Hostname: page-component-8448b6f56d-xtgtn Total loading time: 0 Render date: 2024-04-23T22:49:47.693Z Has data issue: false hasContentIssue false
  • English
  • Français

Class number of (v, n, M)-extensions

Published online by Cambridge University Press:  17 April 2009

Osama Alkam  and
Mehpare Bilhan
Osama Alkam
Affiliation:
Department of Mathematics, College of Science, University of Petra, Amman, Jordan
Mehpare Bilhan
Affiliation:
Department of Mathematics, Faculty of Science and Arts, Middle East Technical University, Ankara, Turkey
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An analogue of cyclotomic number fields for function fields over the finite field q, was investigated by L. Carlitz in 1935 and has been studied recently by D. Hayes, M. Rosen, S. Galovich and others. For each nonzero polynomial M in q [T], we denote by k (ΛM) the cyclotomic function field associated with M, where k = q(T). Replacing T by 1/T in k and considering the cyclotomic function field Fv that corresponds to (1/T)v+1 gets us an extension of k, denoted by Lv, which is the fixed field of Fv modulo 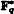. We define a (v, n, M)-extension to be the composite N = knk (Λm) Lv where kn is the constant field of degree n over k. In this paper we give analytic class number formulas for (v, n, M)-extensions when M has a nonzero constant term.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 63 , Issue 1 , February 2001 , pp. 21 - 34
Copyright
Copyright © Australian Mathematical Society 2001

References

[1]Bilhan, M., ‘Arithmetic progressions of polynomials over a finite field’, in Number theory and its applications (Ankara 1996), Lecture Notes in Pure and Applied Mathematics 204 (Dekker, New York, 1999), pp. 1–21.Google Scholar
[2]Carlitz, L., ‘On certain functions connected with polynomials in a Galois field’, Duke Math J. 1 (1935), 137–168.CrossRefGoogle Scholar
[3]Galovich, S. and Rosen, M., ‘The class number of cyclotomic function fields’, J. Number Theory 13 (1981), 363–375.CrossRefGoogle Scholar
[4]Hayes, D. R., ‘Explicit class field theory for rational functional fields’, Trans. Amer. Math. Soc. 189 (1974), 77–91.CrossRefGoogle Scholar
[5]Weil, A., Basic number theory (Springer-Verlag, Berlin, Heidelberg, New York, 1973).CrossRefGoogle Scholar