Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
LORENSEN, KARL
2015.
‘COHOMOLOGY AND PROFINITE TOPOLOGIES FOR SOLVABLE GROUPS OF FINITE RANK’.
Bulletin of the Australian Mathematical Society,
Vol. 91,
Issue. 2,
p.
351.

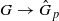 induces an isomorphism
induces an isomorphism 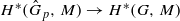 for any discrete
for any discrete 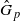 -module
-module 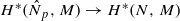 is an isomorphism for any discrete
is an isomorphism for any discrete 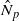 -module
-module 