No CrossRef data available.
Article contents
COMPARING THE GENERALISED ROUNDNESS OF METRIC SPACES
Published online by Cambridge University Press: 02 November 2016
Abstract
Motivated by the local theory of Banach spaces, we introduce a notion of finite representability for metric spaces. This allows us to develop a new technique for comparing the generalised roundness of metric spaces. We illustrate this technique by applying it to Banach spaces and metric trees. In the realm of Banach spaces we obtain results such as the following: (1) if 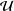 ${\mathcal{U}}$ is any ultrafilter and
${\mathcal{U}}$ is any ultrafilter and 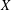 $X$ is any Banach space, then the second dual
$X$ is any Banach space, then the second dual 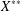 $X^{\ast \ast }$ and the ultrapower
$X^{\ast \ast }$ and the ultrapower 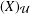 $(X)_{{\mathcal{U}}}$ have the same generalised roundness as
$(X)_{{\mathcal{U}}}$ have the same generalised roundness as 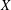 $X$ , and (2) no Banach space of positive generalised roundness is uniformly homeomorphic to
$X$ , and (2) no Banach space of positive generalised roundness is uniformly homeomorphic to 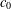 $c_{0}$ or
$c_{0}$ or 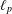 $\ell _{p}$ ,
$\ell _{p}$ , 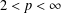 $2<p<\infty$ . For metric trees, we give the first examples of metric trees of generalised roundness one that have finite diameter. In addition, we show that metric trees of generalised roundness one possess special Euclidean embedding properties that distinguish them from all other metric trees.
$2<p<\infty$ . For metric trees, we give the first examples of metric trees of generalised roundness one that have finite diameter. In addition, we show that metric trees of generalised roundness one possess special Euclidean embedding properties that distinguish them from all other metric trees.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © 2016 Australian Mathematical Publishing Association Inc.

