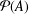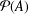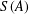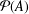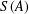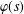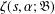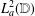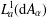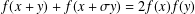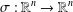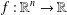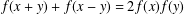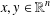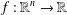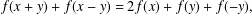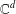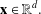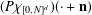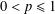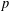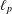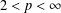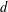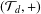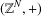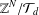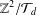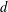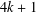Contents
Research Article
A FINITE-TO-ONE MAP FROM THE PERMUTATIONS ON A SET
- Part of:
-
- Published online by Cambridge University Press:
- 19 October 2016, pp. 177-182
-
- Article
-
- You have access
- Export citation
ON A PROBLEM OF ERDÖS AND MAHLER CONCERNING CONTINUED FRACTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 19 October 2016, pp. 183-186
-
- Article
-
- You have access
- Export citation
REMARKS ON THE MIXED JOINT UNIVERSALITY FOR A CLASS OF ZETA FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 19 October 2016, pp. 187-198
-
- Article
-
- You have access
- Export citation
ON PAIRS OF GOLDBACH–LINNIK EQUATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 19 October 2016, pp. 199-208
-
- Article
-
- You have access
- Export citation
FIXED ELEMENTS OF NONINJECTIVE ENDOMORPHISMS OF POLYNOMIAL ALGEBRAS IN TWO VARIABLES
- Part of:
-
- Published online by Cambridge University Press:
- 20 October 2016, pp. 209-213
-
- Article
-
- You have access
- Export citation
A PRIME ESSENTIAL RING THAT GENERATES A SPECIAL ATOM
- Part of:
-
- Published online by Cambridge University Press:
- 02 November 2016, pp. 214-218
-
- Article
-
- You have access
- Export citation
SEMIPERMUTABILITY IN GENERALISED SOLUBLE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 02 November 2016, pp. 219-227
-
- Article
-
- You have access
- Export citation
LOGARITHMIC COEFFICIENTS OF SOME CLOSE-TO-CONVEX FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 02 November 2016, pp. 228-237
-
- Article
-
- You have access
- Export citation
SOME NORMALITY CRITERIA AND A COUNTEREXAMPLE TO THE CONVERSE OF BLOCH’S PRINCIPLE
- Part of:
-
- Published online by Cambridge University Press:
- 23 November 2016, pp. 238-249
-
- Article
-
- You have access
- Export citation
THE HILBERT–SCHMIDT NORM OF A COMPOSITION OPERATOR ON THE BERGMAN SPACE
- Part of:
-
- Published online by Cambridge University Press:
- 02 November 2016, pp. 250-259
-
- Article
-
- You have access
- Export citation
ON THE REAL-VALUED GENERAL SOLUTIONS OF THE D’ALEMBERT EQUATION WITH INVOLUTION
-
- Published online by Cambridge University Press:
- 23 November 2016, pp. 260-268
-
- Article
-
- You have access
- Export citation
TWO NEW GENERALISED HYPERSTABILITY RESULTS FOR THE DRYGAS FUNCTIONAL EQUATION
- Part of:
-
- Published online by Cambridge University Press:
- 09 January 2017, pp. 269-280
-
- Article
-
- You have access
- Export citation
CHARACTERISATIONS OF PARTITION OF UNITIES GENERATED BY ENTIRE FUNCTIONS IN
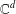 $\mathbb{C}^{d}$
$\mathbb{C}^{d}$
- Part of:
-
- Published online by Cambridge University Press:
- 05 January 2017, pp. 281-290
-
- Article
-
- You have access
- Export citation
MAPPINGS OF CONSERVATIVE DISTANCES IN
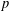 $p$ -NORMED SPACES (
$p$ -NORMED SPACES ( 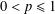 $0<p\leq 1$ )
$0<p\leq 1$ )
- Part of:
-
- Published online by Cambridge University Press:
- 02 November 2016, pp. 291-298
-
- Article
-
- You have access
- Export citation
COMPARING THE GENERALISED ROUNDNESS OF METRIC SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 02 November 2016, pp. 299-314
-
- Article
-
- You have access
- Export citation
STRUCTURE TOPOLOGY AND EXTREME OPERATORS
- Part of:
-
- Published online by Cambridge University Press:
- 19 October 2016, pp. 315-321
-
- Article
-
- You have access
- Export citation
OPERATOR QUASILINEARITY OF SOME FUNCTIONALS ASSOCIATED WITH DAVIS–CHOI–JENSEN’S INEQUALITY FOR POSITIVE MAPS
- Part of:
-
- Published online by Cambridge University Press:
- 19 October 2016, pp. 322-332
-
- Article
-
- You have access
- Export citation
A PURELY METRIC PROOF OF THE CARISTI FIXED POINT THEOREM
- Part of:
-
- Published online by Cambridge University Press:
- 02 November 2016, pp. 333-337
-
- Article
-
- You have access
- Export citation
ALGEBRAIC AND GEOMETRIC PROPERTIES OF LATTICE WALKS WITH STEPS OF EQUAL LENGTH
- Part of:
-
- Published online by Cambridge University Press:
- 02 November 2016, pp. 338-346
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD Theses
TOPOLOGY OF COMPLEX NETWORKS: MODELS AND ANALYSIS
- Part of:
-
- Published online by Cambridge University Press:
- 05 January 2017, pp. 347-349
-
- Article
-
- You have access
- Export citation