Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-27T23:25:18.156Z Has data issue: false hasContentIssue false
  • English
  • Français

ERGODIC EXTENSIONS OF ENDOMORPHISMS

Part of: Selfadjoint operator algebras Individual linear operators as elements of algebraic systems Ergodic theory

Published online by Cambridge University Press:  02 October 2015

EVGENIOS T. A. KAKARIADIS  and
JUSTIN R. PETERS
EVGENIOS T. A. KAKARIADIS*
Affiliation:
School of Mathematics and Statistics, Newcastle University, Newcastle upon Tyne, NE1 7RU, UK email evgenios.kakariadis@ncl.ac.uk
JUSTIN R. PETERS
Affiliation:
Department of Mathematics, Iowa State University, Ames, Iowa, IA 50011, USA email peters@iastate.edu
*
✉evgenios.kakariadis@ncl.ac.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We examine a class of ergodic transformations on a probability measure space 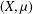$(X,{\it\mu})$ and show that they extend to representations of 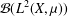${\mathcal{B}}(L^{2}(X,{\it\mu}))$ that are both implemented by a Cuntz family and ergodic. This class contains several known examples, which are unified in our work. During the analysis of the existence and uniqueness of this Cuntz family, we find several results of independent interest. Most notably, we prove a decomposition of 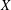$X$ for 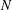$N$-to-one local homeomorphisms that is connected to the orthonormal bases of certain Hilbert modules.

Keywords

maximal abelian selfadjoint algebrasergodic transformationsHilbert modules

MSC classification

Primary: 47C15: Operators in $C^*$- or von Neumann algebras
Secondary: 37A55: Relations with the theory of $C^*$-algebras 46L55: Noncommutative dynamical systems
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 93 , Issue 2 , April 2016 , pp. 307 - 320
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Courtney, D., Muhly, P. S. and Schmidt, W., ‘Composition operators and endomorphisms’, Complex Anal. Oper. Theory 6(1) (2012), 163–188.Google Scholar
Cuntz, J., ‘Simple C*-algebras generated by isometries’, Comm. Math. Phys. 57(2) (1977), 173–185.Google Scholar
Exel, R., ‘A new look at the crossed-product of a C ∗ -algebra by an endomorphism’, Ergodic Theory Dynam. Systems 23(6) (2003), 1733–1750.Google Scholar
Gipson, P., ‘Invariant basis number for C*-algebras’, Preprint, 2014, arXiv:1407.4713.CrossRefGoogle Scholar
Kakariadis, E. T. A. and Katsoulis, E. G., ‘Isomorphism invariants for multivariable C*-dynamics’, J. Noncommut. Geom. 8(3) (2014), 771–787.Google Scholar
Kakariadis, E. T. A. and Peters, J. R., ‘Representations of C*-dynamical systems implemented by Cuntz families’, Münster J. Math. 6 (2013), 383–411.Google Scholar
Laca, M., ‘Endomorphisms of B(H) and Cuntz algebras’, J. Operator Theory 30 (1993), 85–108.Google Scholar
Lance, C., ‘Hilbert C*-modules’, in: A Toolkit for Operator Algebraists, London Mathematical Society Lecture Note Series, 210 (Cambridge University Press, Cambridge, 1995).Google Scholar
Manuilov, V. M. and Troitsky, E. V., ‘Hilbert C*-modules’, Translations of Mathematical Monographs, 226 (American Mathematical Society, Providence, RI, 2005): translated from the 2001 Russian original by the Authors.Google Scholar
Muhly, P. S. and Solel, B., ‘Quantum markov processes (correspondences and dilations)’, Internat. J. Math. 13(8) (2002), 863–909.Google Scholar
Paschke, W. L., ‘Inner product modules over B*-algebras’, Trans. Amer. Math. Soc. 182 (1973), 443–468.Google Scholar
Stacey, P. J., ‘Crossed products of C*-algebras by *-endomorphisms’, J. Aust. Math. Soc. Ser. A 54 (1993), 204–212.CrossRefGoogle Scholar