Dedicated to Professor Li-xin Xuan for his encouragement
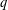 $q$-ADDITIVE FUNCTIONS AND DISTRIBUTIONAL PROPERTIES OF THE LARGEST PRIME FACTOR
$q$-ADDITIVE FUNCTIONS AND DISTRIBUTIONAL PROPERTIES OF THE LARGEST PRIME FACTOR
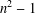 $n^{2}-1$
$n^{2}-1$
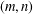 $(m,n)$-JORDAN DERIVATIONS OF RINGS AND BANACH ALGEBRAS
$(m,n)$-JORDAN DERIVATIONS OF RINGS AND BANACH ALGEBRAS
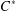 $C^{\ast }$-ALGEBRAS
$C^{\ast }$-ALGEBRAS