Hostname: page-component-5d84bcc8dc-5kdkp Total loading time: 0 Render date: 2026-09-15T21:21:20.789Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE MERTENS–CESÀRO THEOREM FOR NUMBER FIELDS

Part of: Algebraic number theory: global fields

Published online by Cambridge University Press:  11 November 2015

ANDREA FERRAGUTI  and
GIACOMO MICHELI
ANDREA FERRAGUTI
Affiliation:
Institute of Mathematics, University of Zurich, Winterthurerstrasse 190, 8057 Zurich, Switzerland email andrea.ferraguti@math.uzh.ch
GIACOMO MICHELI*
Affiliation:
Institute of Mathematics, University of Zurich, Winterthurerstrasse 190, 8057 Zurich, Switzerland email giacomo.micheli@math.uzh.ch
*
✉giacomo.micheli@math.uzh.ch
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the 'Save PDF' action button.

Let 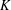$K$ be a number field with ring of integers 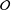${\mathcal{O}}$. After introducing a suitable notion of density for subsets of 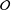${\mathcal{O}}$, generalising the natural density for subsets of 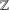$\mathbb{Z}$, we show that the density of the set of coprime 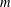$m$-tuples of algebraic integers is 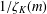$1/{\it\zeta}_{K}(m)$, where 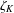${\it\zeta}_{K}$ is the Dedekind zeta function of 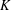$K$. This generalises a result found independently by Mertens [‘Ueber einige asymptotische Gesetze der Zahlentheorie’, J. reine angew. Math. 77 (1874), 289–338] and Cesàro [‘Question 75 (solution)’, Mathesis 3 (1883), 224–225] concerning the density of coprime pairs of integers in 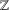$\mathbb{Z}$.

Keywords

number fieldsalgebraic integersnatural densityMertens–Cesàro theoremzeta function

MSC classification

Primary: 11R45: Density theorems
Secondary: 11R04: Algebraic numbers; rings of algebraic integers

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 93 , Issue 2 , April 2016 , pp. 199 - 210
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Barroero, F., Frei, C. and Tichy, R., ‘Additive unit representations in rings over global fields – a survey’, Publ. Math. Debrecen 79(3) (2011), 291–307.CrossRefGoogle Scholar
Cellarosi, F. and Vinogradov, I., ‘Ergodic properties of k-free integers in number fields’, J. Mod. Dyn. 7(3) (2013), 461–488.CrossRefGoogle Scholar
Cesàro, E., ‘Question proposée 75’, Mathesis 1 (1881), 184.Google Scholar
Cesàro, E., ‘Question 75 (solution)’, Mathesis 3 (1883), 224–225.Google Scholar
Hardy, G. H. and Wright, E. M., An Introduction to the Theory of Numbers (Clarendon Press, Oxford, 1960).Google Scholar
Masser, D. and Vaaler, J. D., ‘Counting algebraic numbers with large height II’, Trans. Amer. Math. Soc. 359(1) (2007), 427–445.Google Scholar
Maze, G., Rosenthal, J. and Wagner, U., ‘Natural density of rectangular unimodular integer matrices’, Linear Algebra Appl. 434(5) (2011), 1319–1324.CrossRefGoogle Scholar
Mertens, F., ‘Ueber einige asymptotische Gesetze der Zahlentheorie’, J. reine angew. Math. 77 (1874), 289–338.Google Scholar
Nymann, J. E., ‘On the probability that k positive integers are relatively prime’, J. Number Theory 4(5) (1972), 469–473.Google Scholar
Schanuel, S., ‘Heights in number fields’, Bull. Soc. Math. France 107(4) (1979), 433–449.CrossRefGoogle Scholar
Sittinger, B. D., ‘The probability that random algebraic integers are relatively r-prime’, J. Number Theory 130(1) (2010), 164–171.CrossRefGoogle Scholar