Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-21T10:01:52.405Z Has data issue: false hasContentIssue false
  • English
  • Français

FIBONACCI–MANN ITERATION FOR MONOTONE ASYMPTOTICALLY NONEXPANSIVE MAPPINGS

Part of: Normed linear spaces and Banach spaces; Banach lattices Nonlinear operators and their properties

Published online by Cambridge University Press:  13 March 2017

M. R. ALFURAIDAN  and
M. A. KHAMSI
M. R. ALFURAIDAN
Affiliation:
Department of Mathematics and Statistics, King Fahd University of Petroleum and Minerals, Dhahran 31261, Saudi Arabia email monther@kfupm.edu.sa
M. A. KHAMSI*
Affiliation:
Department of Mathematical Sciences, The University of Texas at El Paso, El Paso, TX 79968, USA email mohamed@utep.edu
*
✉mohamed@utep.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We extend the results of Schu [‘Iterative construction of fixed points of asymptotically nonexpansive mappings’, J. Math. Anal. Appl.158 (1991), 407–413] to monotone asymptotically nonexpansive mappings by means of the Fibonacci–Mann iteration process

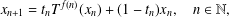$$\begin{eqnarray}x_{n+1}=t_{n}T^{f(n)}(x_{n})+(1-t_{n})x_{n},\quad n\in \mathbb{N},\end{eqnarray}$$
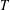where $T$ is a monotone asymptotically nonexpansive self-mapping defined on a closed bounded and nonempty convex subset of a uniformly convex Banach space and 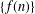$\{f(n)\}$ is the Fibonacci integer sequence. We obtain a weak convergence result in 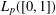$L_{p}([0,1])$, with 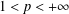$1<p<+\infty$, using a property similar to the weak Opial condition satisfied by monotone sequences.

Keywords

asymptotically nonexpansive mappingFibonacci sequencefixed pointMann iteration processmonotone Lipschitzian mappingOpial conditionuniformly convex Banach space

MSC classification

Primary: 47H09: Contraction-type mappings, nonexpansive mappings, $A$-proper mappings, etc.
Secondary: 46B20: Geometry and structure of normed linear spaces 47H10: Fixed-point theorems
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 2 , October 2017 , pp. 307 - 316
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

Footnotes

The authors acknowledge the support provided by the deanship of scientific research at King Fahd University of Petroleum and Minerals in funding this work through project no. IN141040.

References

Aksoy, A. and Khamsi, M. A., Nonstandard Methods in Fixed Point Theory (Springer, New York, 1990).Google Scholar
Alfuraidan, M. R. and Khamsi, M. A., ‘A fixed point theorem for monotone asymptotically nonexpansive mappings’, Proc. Amer. Math. Soc., to appear.Google Scholar
Beauzamy, B., Introduction to Banach Spaces and Their Geometry (North-Holland, Amsterdam, 1985).Google Scholar
Carl, S. and Heikkilä, S., Fixed Point Theory in Ordered Sets and Applications: From Differential and Integral Equations to Game Theory (Springer, New York, 2011).CrossRefGoogle Scholar
Goebel, K. and Kirk, W. A., ‘A fixed point theorem for asymptotically nonexpansive mappings’, Proc. Amer. Math. Soc. 35 (1972), 171–174.Google Scholar
Jachymski, J., ‘The contraction principle for mappings on a metric space with a graph’, Proc. Amer. Math. Soc. 136 (2008), 1359–1373.Google Scholar
Khamsi, M. A. and Kirk, W. A., An Introduction to Metric Spaces and Fixed Point Theory (John Wiley, New York, 2001).Google Scholar
Opial, Z., ‘Weak convergence of the sequence of successive approximations for nonexpansive mappings’, Bull. Amer. Math. Soc. 73 (1967), 591–597.Google Scholar
Ran, A. C. M. and Reurings, M. C. B., ‘A fixed point theorem in partially ordered sets and some applications to matrix equations’, Proc. Amer. Math. Soc. 132(5) (2004), 1435–1443.Google Scholar
Schu, J., ‘Iterative construction of fixed points of asymptotically nonexpansive mappings’, J. Math. Anal. Appl. 158 (1991), 407–413.Google Scholar