We investigate images of higher-order differential operators of polynomial algebras over a field 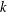 $k$ . We show that, when
$k$ . We show that, when 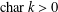 $\operatorname{char}k>0$ , the image of the set of differential operators
$\operatorname{char}k>0$ , the image of the set of differential operators 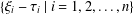 $\{\unicode[STIX]{x1D709}_{i}-\unicode[STIX]{x1D70F}_{i}\mid i=1,2,\ldots ,n\}$ of the polynomial algebra
$\{\unicode[STIX]{x1D709}_{i}-\unicode[STIX]{x1D70F}_{i}\mid i=1,2,\ldots ,n\}$ of the polynomial algebra 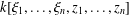 $k[\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{n},z_{1},\ldots ,z_{n}]$ is a Mathieu subspace, where
$k[\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{n},z_{1},\ldots ,z_{n}]$ is a Mathieu subspace, where 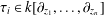 $\unicode[STIX]{x1D70F}_{i}\in k[\unicode[STIX]{x2202}_{z_{1}},\ldots ,\unicode[STIX]{x2202}_{z_{n}}]$ for
$\unicode[STIX]{x1D70F}_{i}\in k[\unicode[STIX]{x2202}_{z_{1}},\ldots ,\unicode[STIX]{x2202}_{z_{n}}]$ for 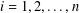 $i=1,2,\ldots ,n$ . We also show that, when
$i=1,2,\ldots ,n$ . We also show that, when 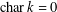 $\operatorname{char}k=0$ , the same conclusion holds for
$\operatorname{char}k=0$ , the same conclusion holds for 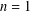 $n=1$ . The problem concerning images of differential operators arose from the study of the Jacobian conjecture.
$n=1$ . The problem concerning images of differential operators arose from the study of the Jacobian conjecture.
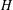 $H$ -FREE GRAPHS
$H$ -FREE GRAPHS
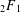 $_{2}F_{1}$
$_{2}F_{1}$
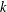 $k$ -GENERALISED FIBONACCI NUMBERS IS DENSE IN
$k$ -GENERALISED FIBONACCI NUMBERS IS DENSE IN 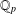 $\mathbb{Q}_{p}$
$\mathbb{Q}_{p}$
 $L$ -FUNCTIONS IN THE EXTENDED SELBERG CLASS
$L$ -FUNCTIONS IN THE EXTENDED SELBERG CLASS