Article contents
THE FINITE BASIS PROBLEM FOR THE MONOID OF TWO-BY-TWO UPPER TRIANGULAR TROPICAL MATRICES
Published online by Cambridge University Press: 08 January 2016
Abstract
For each positive  $n$ , let
$n$ , let 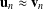 $\mathbf{u}_{n}\approx \boldsymbol{v}_{n}$ denote the identity obtained from the Adjan identity
$\mathbf{u}_{n}\approx \boldsymbol{v}_{n}$ denote the identity obtained from the Adjan identity 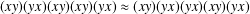 $(xy)(yx)(xy)(xy)(yx)\approx (xy)(yx)(yx)(xy)(yx)$ by substituting
$(xy)(yx)(xy)(xy)(yx)\approx (xy)(yx)(yx)(xy)(yx)$ by substituting 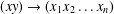 $(xy)\rightarrow (x_{1}x_{2}\ldots x_{n})$ and
$(xy)\rightarrow (x_{1}x_{2}\ldots x_{n})$ and 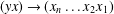 $(yx)\rightarrow (x_{n}\ldots x_{2}x_{1})$ . We show that every monoid which satisfies
$(yx)\rightarrow (x_{n}\ldots x_{2}x_{1})$ . We show that every monoid which satisfies 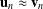 $\mathbf{u}_{n}\approx \boldsymbol{v}_{n}$ for each positive
$\mathbf{u}_{n}\approx \boldsymbol{v}_{n}$ for each positive  $n$ and generates a variety containing the bicyclic monoid is nonfinitely based. This implies that the monoid
$n$ and generates a variety containing the bicyclic monoid is nonfinitely based. This implies that the monoid 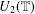 $U_{2}(\mathbb{T})$ (respectively,
$U_{2}(\mathbb{T})$ (respectively, 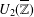 $U_{2}(\overline{\mathbb{Z}})$ ) of two-by-two upper triangular tropical matrices over the tropical semiring
$U_{2}(\overline{\mathbb{Z}})$ ) of two-by-two upper triangular tropical matrices over the tropical semiring 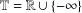 $\mathbb{T}=\mathbb{R}\cup \{-\infty \}$ (respectively,
$\mathbb{T}=\mathbb{R}\cup \{-\infty \}$ (respectively, 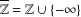 $\overline{\mathbb{Z}}=\mathbb{Z}\cup \{-\infty \}$ ) is nonfinitely based.
$\overline{\mathbb{Z}}=\mathbb{Z}\cup \{-\infty \}$ ) is nonfinitely based.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © 2016 Australian Mathematical Publishing Association Inc.
References
- 12
- Cited by

