Hostname: page-component-8448b6f56d-dnltx Total loading time: 0 Render date: 2024-04-24T12:30:50.533Z Has data issue: false hasContentIssue false
  • English
  • Français

HYPERTRANSCENDENCE OF 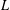$L$-FUNCTIONS FOR 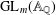$\text{GL}_{m}(\mathbb{A}_{\mathbb{Q}})$

Part of: Zeta and $L$-functions: analytic theory Differential equations in the complex domain

Published online by Cambridge University Press:  11 November 2015

HIROFUMI NAGOSHI
HIROFUMI NAGOSHI*
Affiliation:
Faculty of Science and Technology, Gunma University, Kiryu, Gunma, 376-8515, Japan email nagoshi@gunma-u.ac.jp
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We generalise a result of Hilbert which asserts that the Riemann zeta-function 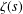${\it\zeta}(s)$ is hypertranscendental over 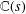$\mathbb{C}(s)$. Let ${\it\pi}$ be any irreducible cuspidal automorphic representation of 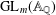$\text{GL}_{m}(\mathbb{A}_{\mathbb{Q}})$ with unitary central character. We establish a certain type of functional difference–differential independence for the associated 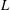$L$-function 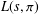$L(s,{\it\pi})$. This result implies algebraic difference–differential independence of 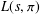$L(s,{\it\pi})$ over 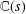$\mathbb{C}(s)$ (and more strongly, over a certain field 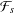${\mathcal{F}}_{s}$ which contains 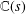$\mathbb{C}(s)$). In particular, 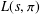$L(s,{\it\pi})$ is hypertranscendental over 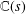$\mathbb{C}(s)$. We also extend a result of Ostrowski on the hypertranscendence of ordinary Dirichlet series.

Keywords

hypertranscendencedifference–differential independenceL-functionDirichlet series

MSC classification

Primary: 11M99: None of the above, but in this section
Secondary: 34M15: Algebraic aspects (differential-algebraic, hypertranscendence, group-theoretical)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 93 , Issue 3 , June 2016 , pp. 388 - 399
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Bank, S. and Kaufman, R., ‘An extension of Hölder’s theorem concerning the Gamma function’, Funkcial. Ekvac. Ser. Int. 19 (1976), 53–63.Google Scholar
Bank, S. and Kaufman, R., ‘A note on Hölder’s theorem concerning the Gamma function’, Math. Ann. 232 (1978), 115–120.CrossRefGoogle Scholar
Chiang, Y. and Feng, S., ‘Difference independence of the Riemann zeta function’, Acta Arith. 125 (2006), 317–329.Google Scholar
Godement, R. and Jacquet, H., Zeta Functions of Simple Algebras, Lecture Notes in Mathematics, 260 (Springer, Berlin, 1972).CrossRefGoogle Scholar
Goldberg, A. A. and Ostrovskii, I. V., Value Distribution of Meromorphic Functions, Translations of Mathematical Monographs, 236 (American Mathematical Society, Providence, RI, 2008).CrossRefGoogle Scholar
Gunning, R. and Rossi, H., Analytic Functions of Several Complex Variables (AMS Chelsea, Providence, RI, 2009), reprint of the 1965 original.CrossRefGoogle Scholar
Hilbert, D., ‘Mathematical problems’, Bull. Amer. Math. Soc. 8 (1902), 437–479 (reprinted); Bull. Amer. Math. Soc. (N.S.) 37(4) (2000), 407–436.CrossRefGoogle Scholar
Hölder, O., ‘Ueber die Eigenschaft der Gammafunction keiner algebraischen Differentialgleichung zu genügen’, Math. Ann. 28 (1886), 1–13.Google Scholar
Jacquet, H. and Shalika, J. A., ‘On Euler products and the classification of automorphic representations I’, Amer. J. Math. 103 (1981), 499–558.Google Scholar
Karatsuba, A. A. and Voronin, S. M., The Riemann Zeta-Function (Walter de Gruyter, Berlin, 1992).CrossRefGoogle Scholar
Laine, I., Nevanlinna Theory and Complex Differential Equations, de Gruyter Studies in Mathematics, 15 (Walter de Gruyter, Berlin, 1993).Google Scholar
Liao, L. and Yang, C., ‘On some new properties of the gamma function and the Riemann zeta function’, Math. Nachr. 257 (2003), 59–66.Google Scholar
Liu, J., Wang, Y. and Ye, Y., ‘A proof of Selberg’s orthogonality for automorphic L-functions’, Manuscripta Math. 118 (2005), 135–149.Google Scholar
Mijajlović, Ž. and Malešević, B., ‘Differentially transcendental functions’, Bull. Belg. Math. Soc. Simon Stevin 15 (2008), 193–201.Google Scholar
Nagoshi, H., ‘On the universality for L-functions attached to Maass forms’, Analysis 25 (2005), 1–22.Google Scholar
Nagoshi, H., ‘The universality of L-functions attached to Maass forms’, Adv. Stud. Pure Math. 49 (2007), 289–306.Google Scholar
Ostrowski, A., ‘Über Dirichletsche Reihen und algebraische Differentialgleichungen’, Math. Z. 8 (1920), 241–298.Google Scholar
Reich, A., ‘Zetafunktionen und Differenzen-Differentialgleichungen’, Arch. Math. 38 (1982), 226–235.CrossRefGoogle Scholar
Reich, A., ‘On hypertranscendental functions’, in: Topics in Classical Number Theory (Colloquium Budapest, 1981), Vol. II, Colloquia Mathematica Societatis János Bolyai, 34 (1984), 1349–1369.Google Scholar
Reich, A., ‘Über Dirichletsche Reihen und holomorphe Differentialgleichungen’, Analysis 4 (1984), 27–44.CrossRefGoogle Scholar
Rudnick, Z. and Sarnak, P., ‘Zeros of principal L-functions and random matrix theory’, Duke Math. J. 81 (1996), 269–322.Google Scholar
Stadigh, V. E. E., ‘Ein Satz Ueber Funktionen, Die Algebraische Differentialgleichungen Befriedigen, Und Ueber Die Eigenschaft Der Function ${\it\zeta}(s)$ Keiner Solchen Gleichung Zu Genügen’; Dissertation, Helsinki, 1902. http://daten.digitale-sammlungen.de/0006/bsb00067906/images.Google Scholar
Steuding, J., Value-Distribution of L-Functions, Lecture Notes in Mathematics, 1877 (Springer, Berlin, 2007).Google Scholar
Voronin, S. M., ‘On the distribution of nonzero values of the Riemann zeta-function’, Proc. Steklov Inst. Math. 128 (1972), 153–175.Google Scholar
Voronin, S. M., ‘On differential independence of 𝜁-functions’, Soviet Math. Dokl. 14 (1973), 607–609.Google Scholar