No CrossRef data available.
Article contents
THE MAXIMAL IDEAL IN THE SPACE OF OPERATORS ON 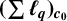 $\boldsymbol {(\sum {\ell }_{q})_{c_{0}}}$
$\boldsymbol {(\sum {\ell }_{q})_{c_{0}}}$
Published online by Cambridge University Press: 21 February 2022
Abstract
We study the isomorphic structure of 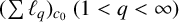 $(\sum {\ell }_{q})_{c_{0}}\ (1< q<\infty )$ and prove that these spaces are complementably homogeneous. We also show that for any operator T from
$(\sum {\ell }_{q})_{c_{0}}\ (1< q<\infty )$ and prove that these spaces are complementably homogeneous. We also show that for any operator T from 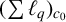 $(\sum {\ell }_{q})_{c_{0}}$ into
$(\sum {\ell }_{q})_{c_{0}}$ into 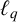 ${\ell }_{q}$, there is a subspace X of
${\ell }_{q}$, there is a subspace X of 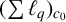 $(\sum {\ell }_{q})_{c_{0}}$ that is isometric to
$(\sum {\ell }_{q})_{c_{0}}$ that is isometric to 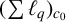 $(\sum {\ell }_{q})_{c_{0}}$ and the restriction of T on X has small norm. If T is a bounded linear operator on
$(\sum {\ell }_{q})_{c_{0}}$ and the restriction of T on X has small norm. If T is a bounded linear operator on 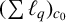 $(\sum {\ell }_{q})_{c_{0}}$ which is
$(\sum {\ell }_{q})_{c_{0}}$ which is 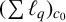 $(\sum {\ell }_{q})_{c_{0}}$-strictly singular, then for any
$(\sum {\ell }_{q})_{c_{0}}$-strictly singular, then for any 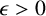 $\epsilon>0$, there is a subspace X of
$\epsilon>0$, there is a subspace X of 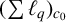 $(\sum {\ell }_{q})_{c_{0}}$ which is isometric to
$(\sum {\ell }_{q})_{c_{0}}$ which is isometric to 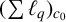 $(\sum {\ell }_{q})_{c_{0}}$ with
$(\sum {\ell }_{q})_{c_{0}}$ with 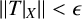 $\|T|_{X}\|<\epsilon $. As an application, we show that the set of all
$\|T|_{X}\|<\epsilon $. As an application, we show that the set of all 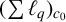 $(\sum {\ell }_{q})_{c_{0}}$-strictly singular operators on
$(\sum {\ell }_{q})_{c_{0}}$-strictly singular operators on 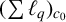 $(\sum {\ell }_{q})_{c_{0}}$ forms the unique maximal ideal of
$(\sum {\ell }_{q})_{c_{0}}$ forms the unique maximal ideal of 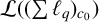 $\mathcal {L}((\sum {\ell }_{q})_{c_{0}})$.
$\mathcal {L}((\sum {\ell }_{q})_{c_{0}})$.
MSC classification
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 106 , Issue 2 , October 2022 , pp. 340 - 348
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
Bentuo Zheng’s research is supported in part by Simons Foundation Grant 585081.


