Hostname: page-component-848d4c4894-ttngx Total loading time: 0 Render date: 2024-06-13T01:41:27.937Z Has data issue: false hasContentIssue false
  • English
  • Français

A NEW MENON’S IDENTITY FROM GROUP ACTIONS

Part of: Elementary number theory Sequences and sets

Published online by Cambridge University Press:  28 November 2018

YU-JIE WANG Open the ORCID record for YU-JIE WANG [Opens in a new window]  and
CHUN-GANG JI Open the ORCID record for CHUN-GANG JI [Opens in a new window]
YU-JIE WANG
Affiliation:
School of Mathematical Sciences, Nanjing Normal University, Nanjing 210023, PR China email wangyujie9291@126.com
CHUN-GANG JI*
Affiliation:
School of Mathematical Sciences, Nanjing Normal University, Nanjing 210023, PR China email cgji@njnu.edu.cn
*
✉cgji@njnu.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $n$ be a positive integer. We obtain new Menon’s identities by using the actions of some subgroups of 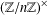$(\mathbb{Z}/n\mathbb{Z})^{\times }$ on the set 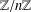$\mathbb{Z}/n\mathbb{Z}$. In particular, let 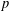$p$ be an odd prime and let $\unicode[STIX]{x1D6FC}$ be a positive integer. If 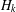$H_{k}$ is a subgroup of 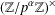$(\mathbb{Z}/p^{\unicode[STIX]{x1D6FC}}\mathbb{Z})^{\times }$ with index 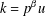$k=p^{\unicode[STIX]{x1D6FD}}u$ such that 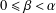$0\leqslant \unicode[STIX]{x1D6FD}<\unicode[STIX]{x1D6FC}$ and 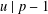$u\mid p-1$, then

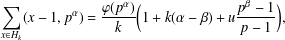$$\begin{eqnarray}\mathop{\sum }_{x\in H_{k}}(x-1,p^{\unicode[STIX]{x1D6FC}})=\frac{\unicode[STIX]{x1D711}(p^{\unicode[STIX]{x1D6FC}})}{k}\bigg(1+k(\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD})+u\frac{p^{\unicode[STIX]{x1D6FD}}-1}{p-1}\bigg),\end{eqnarray}$$
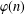where $\unicode[STIX]{x1D711}(n)$ is the Euler totient function.

Keywords

arithmetical sumsMenon’s identitygroup action

MSC classification

Primary: 11A25: Arithmetic functions; related numbers; inversion formulas
Secondary: 11B13: Additive bases, including sumsets
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 99 , Issue 3 , June 2019 , pp. 369 - 375
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

This work was partially supported by the Grant No. 11471162 from NNSF of China and the Specialized Research Fund for the Doctoral Program of Higher Education of China (Grant No. 20133207110012).

References

Jafari, M. H. and Madadi, A. R., ‘On the number of cyclic subgroups of a finite group’, Bull. Korean Math. Soc. 54 (2017), 2141–2147.Google Scholar
Li, Y. and Kim, D., ‘A Menon-type identity with many tuples of group of units in residually finite Dedekind domains’, J. Number Theory 175 (2017), 42–50.Google Scholar
Li, Y. and Kim, D., ‘Menon-type identities derived from actions of subgroups of general linear groups’, J. Number Theory 179 (2017), 97–112.Google Scholar
Menon, P. K., ‘On the sum ∑(a - 1, n)[(a, n) = 1]’, J. Indian Math. Soc. (N.S.) 29 (1965), 155–163.Google Scholar
Miguel, C., ‘Menon’s identity in residually finite Dedekind domains’, J. Number Theory 137 (2014), 179–185.Google Scholar
Miguel, C., ‘A Menon-type identity in residually finite Dedekind domains’, J. Number Theory 164 (2016), 43–51.Google Scholar
Neumann, P., ‘A lemma that is not Burnside’s’, Math. Sci. 4 (1979), 133–141.Google Scholar
Sury, B., ‘Some number-theoretic identities from group actions’, Rend. Circ. Mat. Palermo (2) 58 (2009), 99–108.Google Scholar
Tǎrnǎuceanu, M., ‘A generalization of Menon’s identity’, J. Number Theory 132 (2012), 2568–2573.Google Scholar
Zhang, X. and Ji, C. G., ‘Sums of generators of ideals in residue class ring’, J. Number Theory 174 (2017), 14–25.Google Scholar