Article contents
A NOTE ON GROUPS WHOSE PROPER LARGE SUBGROUPS HAVE A TRANSITIVE NORMALITY RELATION
Published online by Cambridge University Press: 04 November 2016
Abstract
A group 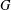 $G$ is said to have the
$G$ is said to have the 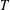 $T$ -property (or to be a
$T$ -property (or to be a 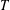 $T$ -group) if all its subnormal subgroups are normal, that is, if normality in
$T$ -group) if all its subnormal subgroups are normal, that is, if normality in 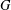 $G$ is a transitive relation. The aim of this paper is to investigate the behaviour of uncountable groups of cardinality
$G$ is a transitive relation. The aim of this paper is to investigate the behaviour of uncountable groups of cardinality 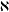 $\aleph$ whose proper subgroups of cardinality
$\aleph$ whose proper subgroups of cardinality 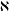 $\aleph$ have a transitive normality relation. It is proved that such a group
$\aleph$ have a transitive normality relation. It is proved that such a group 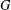 $G$ is a
$G$ is a 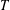 $T$ -group (and all its subgroups have the same property) provided that
$T$ -group (and all its subgroups have the same property) provided that 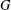 $G$ has an ascending subnormal series with abelian factors. Moreover, it is shown that if
$G$ has an ascending subnormal series with abelian factors. Moreover, it is shown that if 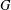 $G$ is an uncountable soluble group of cardinality
$G$ is an uncountable soluble group of cardinality 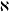 $\aleph$ whose proper normal subgroups of cardinality
$\aleph$ whose proper normal subgroups of cardinality 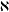 $\aleph$ have the
$\aleph$ have the 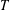 $T$ -property, then every subnormal subgroup of
$T$ -property, then every subnormal subgroup of 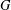 $G$ has only finitely many conjugates.
$G$ has only finitely many conjugates.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © 2016 Australian Mathematical Publishing Association Inc.
References
- 3
- Cited by

