Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gao, Yin-Zhu
and
Shi, Wei-Xue
2015.
Notes on the Collins–Roscoe property and D-spaces.
Topology and its Applications,
Vol. 196,
Issue. ,
p.
448.

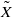 be the minimal dense linearly ordered extension of
be the minimal dense linearly ordered extension of 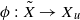 , ϕ(〈
, ϕ(〈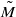 is a paracompact
is a paracompact 