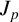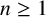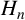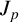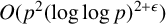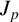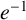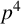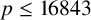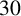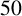1 Introduction
The sequence of harmonic numbers
$$ \begin{align*} H_n=1+\frac12+\frac13+\cdots+\frac1n \end{align*} $$
is a much studied one in the literature, mainly due to its connections with the Riemann zeta function and Bernoulli numbers. Over the centuries, many arithmetic properties of
$H_n$
have been discovered; a well-known example is Wolstenholme’s theorem [Reference Wolstenholme19], which states that
$p^2$
divides the numerator of
$H_{p-1}$
for every prime
$p\geq 5$
. More generally, the divisibility of
$H_n$
by a given prime p has attracted much interest [Reference Altuntaş1, Reference Bayat2, Reference Booker, Hathi, Mossinghoff and Trudgian4, Reference Boyd5, Reference Carlitz7, Reference Eswarathasan and Levine10–Reference Sun and Hong16, Reference Wu and Chen20].
Our motivation for looking into the sequence
$H_n$
is threefold. First, harmonic numbers are related to p-adic L-functions [Reference Washington18], which are less well understood than the classical ones. A striking fact in this context is that we do not even know if p-adic zeta functions are always nonzero on the positive integers (see, for example, [Reference Beukers3, Reference Calegari6]).
Second, the set of harmonic numbers divisible by a given prime p can be described by a probabilistic model, which allows one to make conjectures on what we should expect. This has been worked out in full detail by Boyd [Reference Boyd5].
Third, specialised software is available to test the predictions made by the probabilistic model. As explained by Boyd in [Reference Boyd5, Section 5], the ‘naive’ approach of computing
$H_n$
from
$H_{n-1}$
and then checking the divisibility is unfeasible for large values of n. Instead, a better-tailored p-adic method can reach much higher values.
1.1 The set
$J_p$
The central object in this paper is the set
$$ \begin{align*} J_p := \{n\geq 1:\; \nu_p(H_n)\geq 1\}, \end{align*} $$
where p is a prime and
$\nu _p(a)$
denotes the p-adic valuation of a. In other words,
$J_p$
contains those n such that p divides the numerator of
$H_n$
(when written in lowest terms). We aim to describe the two extreme cases of how small and how large the cardinality
$|J_p|$
can be.
In 1991, Eswarathasan and Levine [Reference Eswarathasan and Levine10] initiated a study of
$J_p$
and computed the full set when
$p=3,5,7$
. Based on the fact that these sets were all finite, they conjectured that this should always be the case (a rather ambitious conjecture, in view of the limited evidence).
Conjecture 1.1. The set
$J_p$
is finite for all primes p.
In the same paper, they showed that for all
$p\geq 5$
, the set
$J_p$
always contains
${p-1}$
,
$p^2-p$
and
$p^2-1$
. They called harmonic primes those p for which
$|J_p|=3$
and suggested that they should occur infinitely often.
Conjecture 1.2. There are infinitely many harmonic primes.
To explore these conjectures, Eswarathasan and Levine devised an algorithm based on the decomposition
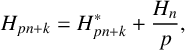$$ \begin{align} H_{pn+k} = H_{pn+k}^* + \frac{H_{n}}{p}, \end{align} $$
where
$k\in [0,p-1]$
and
$H_n^*$
denotes a sum as in
$H_n$
, but restricted to integers coprime to p. Since
$H_{pn+k}^*\equiv H_{k}$
modulo p, it follows from (1.1) that
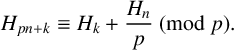$$ \begin{align} H_{pn+k} \equiv H_{k} + \frac{H_n}{p} \pmod{p}. \end{align} $$
Therefore,
$pn+k\in J_p$
if and only if
$n\in J_p$
and
$p^{-1}H_n\equiv -H_k$
modulo p (see [Reference Eswarathasan and Levine10, Theorem 3.1]). In particular, this suggests a search strategy as follows: after computing
$H_k$
modulo p for all
$k=1,\dots ,p-1$
, determine the elements of
$J_p\cap [p^m,p^{m+1}-1)$
and then use the above criterion to find
$J_p\cap [p^{m+1},p^{m+2}-1)$
.
In 1994, Boyd [Reference Boyd5] extended this method by exploiting a p-adically convergent series for
$H_{pn}-p^{-1}H_n$
(see [Reference Boyd5, Theorem 5.2]), which allowed him to essentially iterate the recursion in (1.2) and get back to computing only the initial interval
$J_p\cap [1,p-1]$
, but to a high p-adic precision. He managed to establish that
$J_p$
is finite for all primes
$p \le 547$
except possibly for
$p\in \{83, 127, 397\}$
.
Boyd also explained how the set
$J_p$
can be described in terms of a probabilistic Galton–Watson branching process. Such a random model suggests that, with probability one, the cardinality
$|J_p|$
is indeed finite (in agreement with Conjecture 1.1) and of the order
$O(p^2(\log \log p)^{2+\epsilon })$
, with infinitely many primes satisfying
$|J_p|\geq p^2(\log \log p)^2$
. In addition, Boyd’s model predicts that harmonic primes should have density
$e^{-1}$
among all primes, which gives a quantitative refinement of Conjecture 1.2. Finally, it predicts that
$H_n$
cannot be divisible by high powers of p [Reference Boyd5, page 288].
Conjecture 1.3. There are no pairs
$(p,n)$
with
$\nu _p(H_n)\geq 5$
. The case
$\nu _p(H_n)=4$
, if it occurs at all, should occur only finitely many times.
In contrast, it is very common that
$\nu _p(H_n)\leq 2$
. The case
$\nu _p(H_n)=3$
occurs too, although rarely, the first instance being when
$p=11$
and
$n=848$
.
1.2 Main result
We extend Boyd’s results in two directions. First, in a ‘vertical direction’, so to speak, we consider small primes and check how large
$|J_p|$
can get. For a single prime, this can become very time-consuming and so we decided to stop at
$p=16843$
(the first Wolstenholme prime), extending Boyd’s computations by a factor of approximately 30. In a ‘horizontal direction’, instead, we count harmonic primes up to some large bound. The computation for a single prime in this case is fast and we go up to
$50\times 10^5$
, extending Boyd’s computation by a factor of
$50$
. Our findings are summarised in the following theorem.
Theorem 1.4.
-
(i) For all primes
$p\leq 16843$
, the set
$J_p$
is finite, with at most one exception, namely
$p=1381$
. -
(ii) There are
$128594$
harmonic primes in the interval
$[5,50\times 10^5]$
, corresponding to
$\approx 36.89812\%$
of all primes in this range. -
(iii) There are no pairs
$(p,n)$
with
$p\leq 16843$
,
$p\neq 1381$
, for which
$\nu _p(H_n)\geq 4$
. If any such pair exists when
$p=1381$
, we must have
$n\geq 1381^{3801}$
.
The first point of Theorem 1.4 confirms Conjecture 1.1 for all primes
$p\leq 16843$
, with the exception of
$1381$
. We did not complete the full enumeration of
$J_{1381}$
, since we kept finding new elements all the way up to height
$1381^{3800}$
(and in each of the last twenty p-adic intervals, there are more than
$4000$
elements, suggesting that we are far from completion). A more precise version of point (i) is stated in Observation 2.1, where we explain that
$|J_p|\leq p^2$
for all the primes we examined with four exceptions that satisfy instead the inequality
$|J_p|\geq p^2(\log \log p)^2$
. This is in agreement with Boyd’s quantitative version of Conjecture 1.1. In Observation 2.3, we also discuss the extinction time of
$J_p$
, namely the largest power of p needed to visit the whole set, and compare it with the predictions from the model (see [Reference Boyd5, page 301]).
The second point in Theorem 1.4 (see Observation 2.2) is in agreement with the prediction that harmonic primes should have density
$e^{-1}=0.3678794411\dots $
among all primes and hints at the correctness of Conjecture 1.2. Figure 2 shows the fluctuations around the value
$e^{-1}$
.
Finally, in the last point of Theorem 1.4, we confirm that we never observe a p-adic valuation larger than
$3$
, in agreement with Conjecture 1.3. We found
$21$
elements with valuation
$3$
(see Observation 2.4 and Table 2).
Regarding progress towards a proof of Conjectures 1.1–1.3, Sanna [Reference Sanna15, Theorem 1.1] proved that for any prime p and any
$x\geq 1$
,
$$ \begin{align*} |J_p \cap [1,x]| < 129 \, p^{{2}/{3}} \, x^{0.765}. \end{align*} $$
Although not giving finiteness, this shows that
$J_p$
has density zero in the integers. Sanna’s result has been improved by Wu and Chen [Reference Wu and Chen20, Theorem 1.1] to
$$ \begin{align*} |J_p\cap [1,x]|\leq 3 \, x^{{2}/{3} + {1}/{25\log p}}. \end{align*} $$
Bounds of this type have also been proved for harmonic numbers of exponent greater than one by Altuntaş [Reference Altuntaş1, Theorem A]. As for the possibility of having large p-adic valuation, De Filpo and the first and third authors showed that if
$p\nmid n$
and
$\nu _p(H_n)$
equals
$3$
or
$4$
([Reference Carofiglio, De Filpo and Gambini8, Theorems 2.5 and 2.6], respectively), then
$\nu _p(H_{p^mn})$
grows linearly in m before going down again to something
$\leq 2$
. If we believe Conjecture 1.3 is correct, then we should expect that the descent occurs immediately. Our data confirm this, as we can see from Table 2 where no two consecutive values of m appear.
All computations were made with pari/gp [17]; source code is available online [Reference Cherubini9].
2 Proof of Theorem 1.4
We wish to understand whether
$J_p$
is finite or not, what is the largest size
$J_p$
can reach as p varies, and what is the largest p-adic valuation of its elements. Our first step consists in splitting the integers in p-adic blocks and checking the divisibility of harmonic numbers in each block. Let
$m\geq 1$
and define the mth p-adic block of
$J_p$
as
$$ \begin{align*} J_{p,m} := J_p \cap [p^{m-1},p^{m}-1]. \end{align*} $$
Clearly,
$J_p$
is the union of the sets
$J_{p,m}$
as m varies. Moreover, as explained by Boyd in [Reference Boyd5, Section 3],
$J_p$
has a recursive structure, so that its mth block can be obtained from the previous one, provided we understand the latter sufficiently well. To see this, let
$k\in [0,p-1]$
and set
$H_0=0$
. By [Reference Boyd5, Lemma 3.1],
$$ \begin{align} H_{pn+k} = H_{pn} + H_{k} + O(p) = \frac{H_n}{p} + H_k + O(p). \end{align} $$
Here and in the rest of the paper, we use the convention that something is
$O(p^s)$
if it is divisible by
$p^s$
. Therefore, if we know
$H_n$
up to an error
$O(p^2)$
for all
${n\in [p^{m-1}, p^m-1]}$
, as well as the value of
$H_k$
up to an error
$O(p)$
for all
$k\in [0,p-1]$
, we can determine if
$H_{pn+k}$
is a p-adic integer and if
$\nu _p(H_{pn+k})\geq 1$
for all integers
$pn+k\in [p^{m},p^{m+1}-1]$
. In particular, (2.1) implies that if
$\nu _p(H_n)\leq 0$
for all integers n in a given p-adic block, then for all integers in the next block, we have again
$\nu _p(H_{n})\leq 0$
. In turn, this shows that the finiteness of
$J_p$
is equivalent to showing that
$J_{p,m}=\emptyset $
for some
$m\geq 1$
, that is, eventually there is an empty block.
By the above discussion, it follows that the elements of
$J_p$
can be arranged in a tree, where the nodes at level m are those n in the interval
$[p^{m-1},p^m-1]$
with
$\nu _p(H_n)\geq 1$
and for every integer
$k\in [0,p-1]$
, there is an edge from n to
$pn+k$
if and only if
$H_n\equiv -p H_k\bmod {p^2}$
. The set of residues
$R=\{H_k\bmod {p}\}$
plays an important role in the structure of such a tree. Assuming that the elements in R are essentially randomly distributed, Boyd [Reference Boyd5, Sections 3 and 6–7] gave a heuristic argument that suggests that for every fixed
$\epsilon>0$
, we should have
$$ \begin{align*} |J_p| \ll_\epsilon p^2(\log\log p)^{2+\epsilon} \end{align*} $$
for all primes, although there should be infinitely many primes for which
$$ \begin{align} |J_p|> p^2(\log\log p)^2. \end{align} $$
Boyd computed
$J_p$
for all primes
$p<550$
and his results were consistent with these predictions. In particular, he found that
$|J_{11}|=638>11^2$
, giving one instance of (2.2). When
$p=83,127$
and
$397$
, he could not determine the set
$J_p$
in full, but obtained lower bounds on
$|J_p|$
by looking at p-adic blocks
$J_{p,m}$
with
$m\leq 100$
(see [Reference Boyd5, page 288]). We complete the computation for these three primes and go further, up to the first Wolstenholme prime, obtaining the following observation.
Observation 2.1. For
$5\leq p\leq 16843$
, we have
$|J_p|\leq p^2$
, unless
$p=11,83,397$
or
$1381$
, in which case, we have
$$ \begin{align} |J_{11}|=638,\quad |J_{83}|=43038,\quad |J_{397}|=701533,\quad |J_{1381}|\geq 7521563. \end{align} $$
The prime
$p=127$
completes with precision
$m=146$
and gives
$|J_{127}|=3515$
. When
$p=1381$
, we could not complete the determination of
$J_p$
(we reached precision
$3800$
) and that is why we only have a lower bound in (2.3).
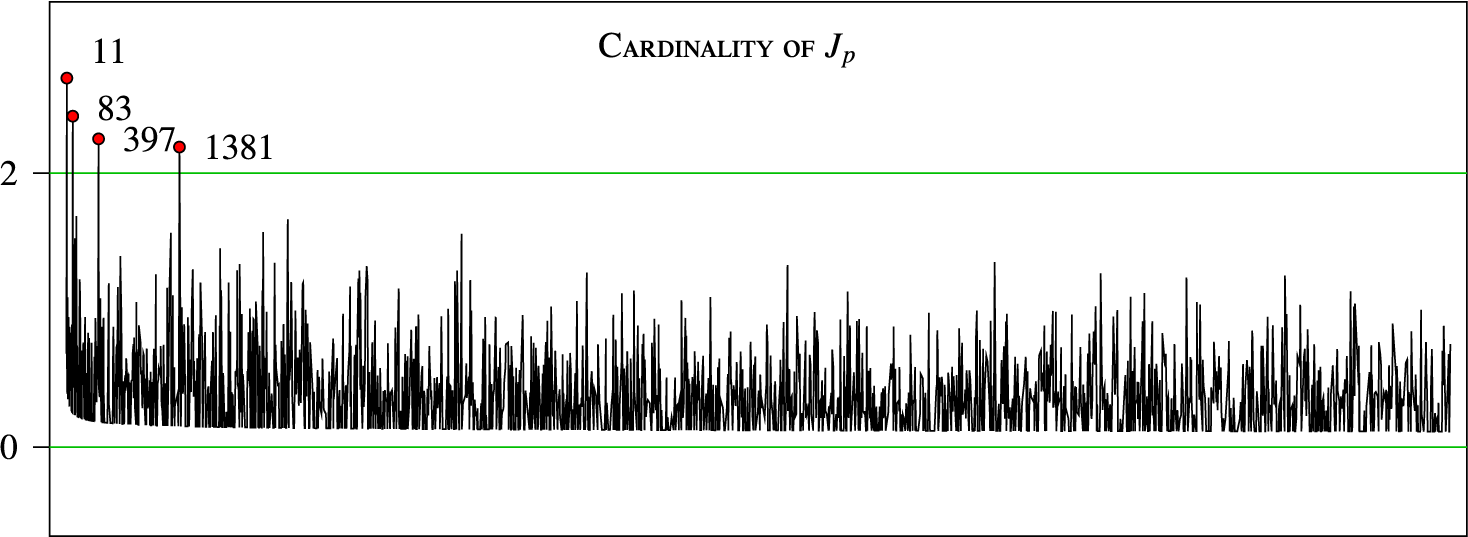
Figure 1 Cardinality of
$J_p$
on a logarithmic scale. On the horizontal axis, we have
$5\leq p\leq 16843$
and on the vertical axis, the quantity
$\log |J_p|/\!\log p$
. The profile on the bottom corresponds to the curve
$\log 3/\!\log p$
associated with harmonic primes for which
$|J_p|=3$
.
One can also look at how the cardinalities
$|J_p|$
distribute as p varies (see Figure 1). They certainly do not distribute uniformly, but rather tend to favour small numbers. For instance, more than sixty percent of all primes
$p\leq 16843$
have
$|J_p|\leq 31$
and approximately
$36$
percent have
$|J_p|=3$
. In Table 1, the distribution among the observed cardinalities up to
$31$
is given. Curiously, in this range, not all integers are observed. For instance, there is no prime
$p\leq 16843$
with
$|J_p|=5$
. Another visible feature is that most observed integers are odd. This can partly be explained by Boyd’s probabilistic model: apart from the set
$J_{p,1}$
which often contains the single element
$p-1$
, the model predicts that at each successive level
$J_{p,m}$
, an even number of elements is generated [Reference Boyd5, Section 6.2], making the total count odd. We indeed observe such a parity phenomenon in most levels. Nevertheless, there are some primes with
$|J_p|$
even, too.
Table 1 For
$3\leq N\leq 31$
, count of primes
$5\leq p\leq 16843$
with
$|J_p|=N$
and corresponding percentage of the total (the last digit is rounded down). The values
$18,20,24,26$
occur exactly once and are omitted. No other
$N\leq 30$
appears. Values above
$31$
appear less than
$19$
times each (less than
$1\%$
of the total) and are omitted.
The case
$|J_p|=3$
is special. For every
$p\geq 5$
, Eswarathasan and Levine [Reference Eswarathasan and Levine10] showed that
$J_p$
contains
$p-1,p^2-1,p^2-p$
and therefore
$|J_p|\geq 3$
. As we explained in the introduction, they called those primes for which equality holds ‘harmonic primes’. Table 1 shows that out of
$1942$
primes in the interval
$[5,16843]$
, approximately
$36.35$
percent are harmonic. Boyd’s model predicts that harmonic primes should have density
$e^{-1}=0.36787944\dots $
among all primes [Reference Boyd5, Section 4]. He computed harmonic primes up to
$10^{5}$
, which agreed with such a prediction, although he writes that ‘the number of harmonic primes in a given interval is perhaps somewhat higher than expected’.
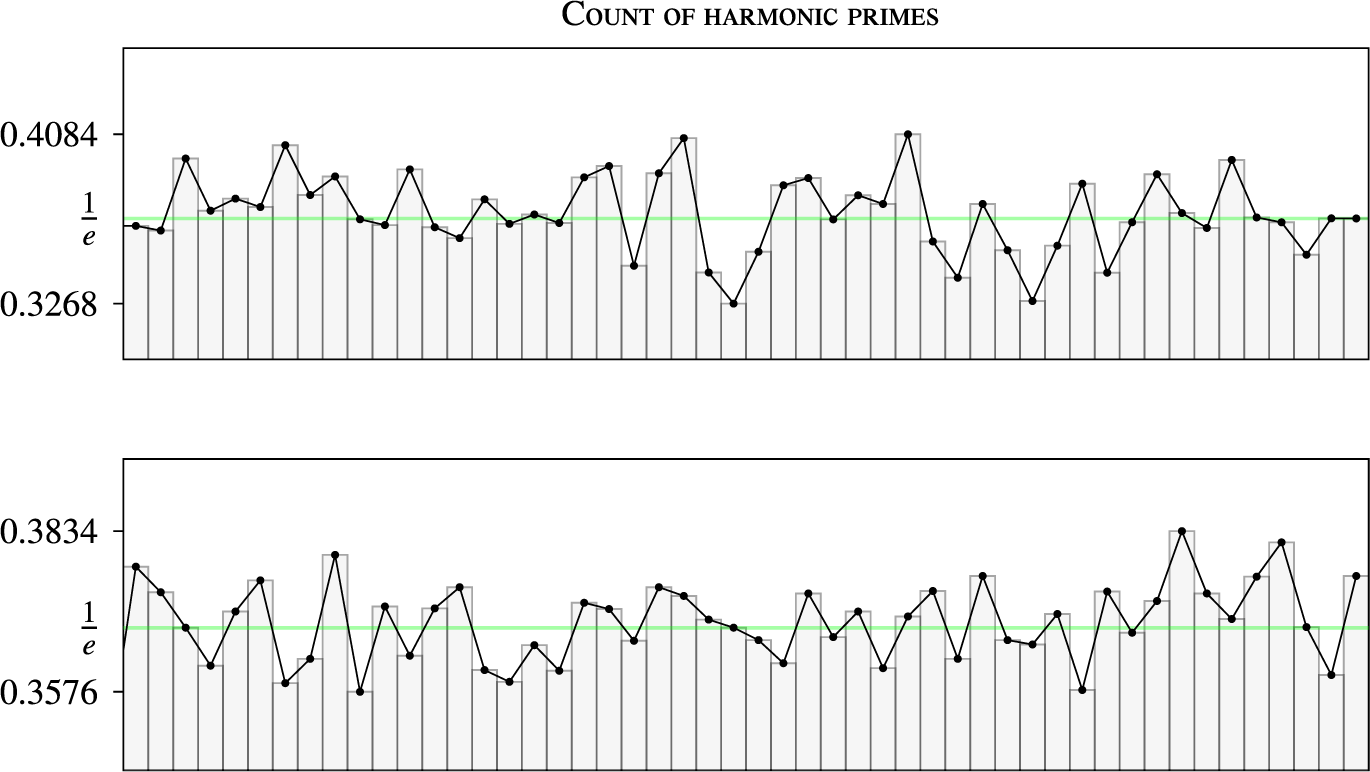
Figure 2 Count of harmonic primes in
$50$
intervals of size
$10^4$
(top) and of size
$10^5$
(bottom). In the top part, the first 10 columns correspond to [Reference Boyd5, Table 1]. The value
$e^{-1}\approx 0.367879$
is the density predicted by Boyd’s probabilistic model.
We extend Boyd’s computation to primes up to
$50\times 10^5$
and in Figure 2, we plot the ratio of harmonic primes in fifty intervals of size
$10^4$
(top) and of size
$10^5$
(bottom) over all primes in the same interval. There are fluctuations around the value
$e^{-1}$
, but it seems very convincing that this should be the correct density. For instance, in the interval
$[490000,500000]$
, the fit is so accurate that we find
$284$
harmonic primes out of
$772$
primes, for a ratio of
$$ \begin{align*} \tfrac{284}{772} = 0.367875647\dots \end{align*} $$
which agrees with
$e^{-1}$
to the fifth decimal digit. As for the total count, we have the following observation.
Observation 2.2. Out of
$348511$
primes
$p\in [5,50\times 10^5]$
,
$128594$
are harmonic, giving a ratio
$128594/348511\approx 0.3689812$
.
Returning to (2.1), let us explain how the set
$J_p$
is computed. From (2.1), we see that
$H_{pn}-H_n/p$
is a p-adic integer with valuation at least one. More is true: there exists a sequence of p-adic numbers
$\{c_k\}_{k\geq 1}$
such that for all integers
$n\geq 1$
,
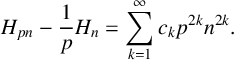$$ \begin{align} H_{pn}-\frac{1}{p}H_n = \sum_{k=1}^\infty c_k p^{2k} n^{2k}. \end{align} $$
The numbers
$c_k$
are p-adic integers unless
$(p-1) \mid 2k$
or
$p \mid k$
and, in general, we have
$v_p(c_k)-1+v_p(1/k)$
in the first case,
$v_p(c_k)=v_p(1/k)$
otherwise. This is proved in [Reference Boyd5, Theorem 5.2]. We use (2.4) to compute harmonic numbers as follows. First, we compute the numbers
$b_n=H_{pn}-H_n/p$
for
$n=1,\dots ,N$
, to a p-adic precision s, and then solve the linear system
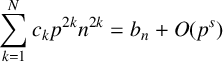$$ \begin{align} \sum_{k=1}^{N} c_k p^{2k} n^{2k} = b_n +O(p^s) \end{align} $$
in
$c_1p^2,\dots ,c_Np^{2N}$
. The matrix of this system is the Vandermonde matrix V, whose inverse satisfies
$\nu _p(V^{-1})>-2N/(p-1)$
, so that the unknowns
$c_kp^{2k}$
are obtained to precision
$s-2N/(p-1)$
. For fixed N, the sum on the left in (2.5) represents
$b_n$
to precision [Reference Boyd5, Remark 3]
$$ \begin{align*} s = \min_{k>N} (\nu_p(c_k)+2k) \geq 2N+2-[\log_p(N+1)]. \end{align*} $$
An algorithm to calculate
$J_p$
starts by computing
$b_n=H_{pn}-H_n/p$
for
$n\leq N$
and finding the coefficients
$c_k'=c_kp^{2k}$
to precision
$s\geq 2N+2-[\log _p(N+1)]$
as explained above. In the process, we have computed
$H_n$
for
$1\leq n\leq p-1$
to precision at least s and hence will know
$J_{p,1}$
. Then, once we have the elements at a given level
$J_{p,m}$
to a precision
$r\leq s$
, we compute
$H_{pn}$
from (2.4) to precision
$r-1$
and then compute
$H_{pn+k}=H_{pn+k-1}+1/(pn+k)$
for
$k=1,\dots ,p-1$
, thus obtaining
$J_{p,m+1}$
to precision
$r-1$
.
Notice that the precision decreases by one at each new level and so we can calculate elements in
$J_p$
up to the sth block
$J_{p,s}$
. If this set is empty, then we are done and we have found all elements in
$J_p$
, which is finite. If
$J_{p,s}$
is not empty, we begin the computation again with a larger value of N.
As pointed out in [Reference Boyd5, Section 5], this method is faster than the ‘naive’ method of computing harmonic numbers with the recursion
$H_n=H_{n-1}+1/n$
. For instance, from [Reference Boyd5], the naive method could not complete the full determination of
$J_{11}$
, which has 638 elements and contains integers as large as
$11^{30}$
, whereas the p-adic method described above succeeds and can go much further than that.
When running the algorithm with precision s, if
$J_{p,s}\neq \emptyset $
, we need to go back to the beginning and repeat the computation with a higher precision. To speed up successive computations, we observe that at each level, not all nodes have children and so it is not necessary to compute all elements in
$J_p$
, but only those that have descendants in the sth block
$J_{p,s}$
. This yields quite a bit of time and memory saving. For instance, when
${p=1381}$
, we find that
$J_{1381,s}$
is nonempty for all
$s\leq 3800$
. If we look at intermediate levels, we notice that
$|J_{1381,1663}|=2501$
, but only one element in this block has descendants all the way down to
$J_{1381,3800}$
. Therefore, when running the algorithm for any
$s\geq 3800$
, it suffices to calculate one element in each
$J_{1381,r}$
for all
$r\leq 1663$
, for a total of
$1663$
harmonic numbers instead of
$|J_{1381,1}\cup \cdots \cup J_{1381,1663}|=1860315$
elements.
In Figure 3, we plot the precision required to compute
$J_p$
for all primes
$p\leq 16843$
. This is sometimes referred to as the ‘extinction time’ for the branching process associated to
$J_p$
. Similarly as with the cardinality, the random model predicts that the extinction time should always be
$O(p(\log \log p)^{1+\epsilon })$
, but there should be infinitely many primes with extinction time larger than
$p\log \log p$
.
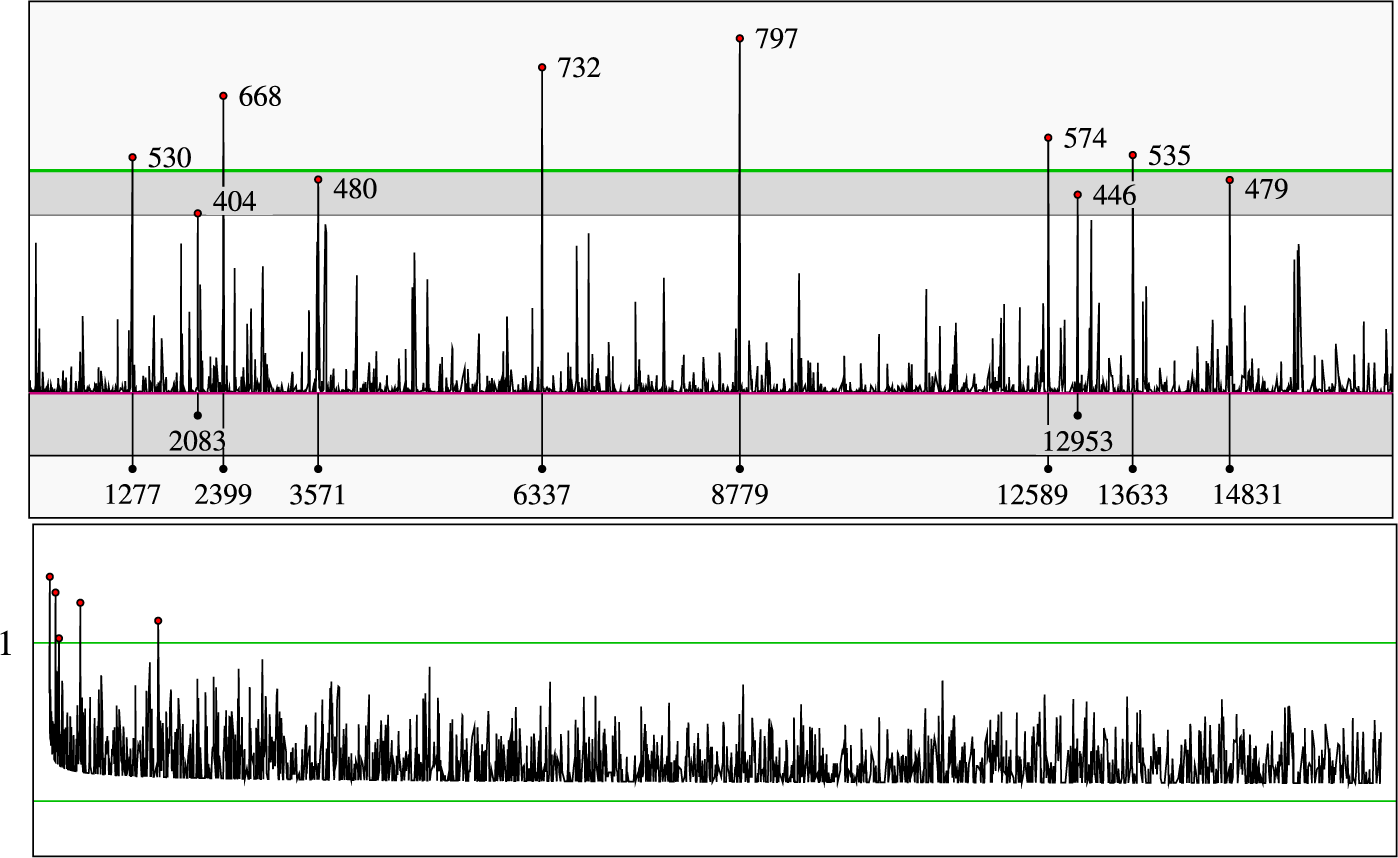
Figure 3 For primes
$5\leq p\leq 16843$
, we plot the extinction time
$M_p$
(top figure:
$p=397,1381,2699,4813,11299$
are omitted) and in logarithmic scale we plot
$\log M_p/\!\log p$
(bottom figure, including all primes).
We see from Figure 3 that the extinction time is indeed often large, say larger than 400. However, very few primes have an extinction time as large as
$p\log \log p$
and it does not come as a surprise that they are essentially the same ones for which the cardinality is exceptionally large. In fact, in the top part of the figure, the primes
${p=397}$
and
$1381$
are omitted, since their extinction time is much higher than all other primes (respectively
$1814$
and more than
$3801$
). We also omit the primes
$2699$
,
$4813$
and
$11299$
, whose extinction times are respectively
$1186$
,
$1336$
and
$1214$
. The peaks in the bottom part of Figure 3 correspond to
$p=11,83,127,397$
and
$1381$
. Summarising, we have the following observation.
Observation 2.3. The extinction time
$M_p$
satisfies
$M_p\leq p$
for all primes
$p\leq 16843$
, with the following exceptions:
$$ \begin{align*} M_{11}=30,\quad M_{83}=339,\quad M_{127}=146,\quad M_{397}=1815,\quad M_{1381}\geq 3801. \end{align*} $$
We conclude by discussing harmonic numbers with large p-adic valuation. For an integer n to be in
$J_p$
, we must have
$\nu _p(H_n)\geq 1$
and computations reveal many integers for which
$\nu _p(H_n)=2$
. Based on his model, Boyd conjectured that there are primes p for which the number of n such that
$\nu _p(H_n)=3$
is arbitrarily large, but of order between
$(\log \log p)^2$
and
$(\log \log p)^{2+\epsilon }$
. However, he conjectured that
$\nu _p(H_n)\geq 4$
never occurs. In his work, he found no element with valuation
$4$
or higher and only five instances of valuation 3: four when
$p=11$
and one when
$p=83$
. With the new data at hand, we have the following observation.
Observation 2.4.
-
(i) For a given prime
$5\leq p\leq 16843$
, the number of integers n such that
$\nu _p(H_n)=2$
can be as large as
$5314$
. More precisely,
$$ \begin{align*} \max_{5\leq p\leq 16843} |\{n\in J_p:\nu_p(H_n)=2\}| = |\{n\in J_{1381}:\nu_{1381}(H_n)=2\}| \geq 5314. \end{align*} $$
The second largest value is
$1760$
, which is attained when
$p=397$
. -
(ii) There are 21 pairs
$(p,n)$
with
$5\leq p\leq 16843$
for which
$\nu _p(H_n)=3$
and the integers n appear in the p-adic intervals
$J_{p,m}$
described in Table 2. When
${p=1381}$
, possible additional occurrences must have
$n\geq 1381^{3801}$
. -
(iii) There are no pairs
$(p,n)$
with
$5\leq p\leq 16843$
,
$p\neq 1381$
, for which
$\nu _p(H_n)\geq 4$
. If any such pair exists when
$p=1381$
, we must have
$n\geq 1381^{3801}$
.
Notice that when
$p=83$
, the new integers we found with valuation three are all larger than
$p^{107}$
. Since Boyd computed
$J_p$
up to
$p^{100}$
, this explains why they do not appear in his work.
Table 2 For each prime
$p=11,83,397,1381$
, elements with valuation three are found in the intervals
$J_{p,m}$
with m as listed on the right.
Open access
