Hostname: page-component-7dd5485656-glrdx Total loading time: 0 Render date: 2025-10-30T07:16:47.089Z Has data issue: false hasContentIssue false
  • English
  • Français

ON NONINNER AUTOMORPHISMS OF FINITE NONABELIAN 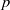$p$-GROUPS

Part of: Representation theory of groups

Published online by Cambridge University Press:  07 June 2013

S. M. GHORAISHI
S. M. GHORAISHI*
Affiliation:
Department of Mathematics, University of Isfahan, 81746-73441, Iran
*
m.ghoraishi@sci.ui.ac.ir
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A long-standing conjecture asserts that every finite nonabelian 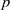$p$-group has a noninner automorphism of order 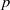$p$. In this paper the verification of the conjecture is reduced to the case of 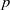$p$-groups 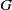$G$ satisfying 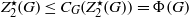${ Z}_{2}^{\star } (G)\leq {C}_{G} ({ Z}_{2}^{\star } (G))= \Phi (G)$, where 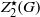${ Z}_{2}^{\star } (G)$ is the preimage of 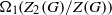${\Omega }_{1} ({Z}_{2} (G)/ Z(G))$ in 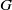$G$. This improves Deaconescu and Silberberg’s reduction of the conjecture: if 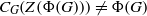${C}_{G} (Z(\Phi (G)))\not = \Phi (G)$, then 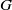$G$ has a noninner automorphism of order 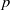$p$ leaving the Frattini subgroup of 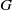$G$ elementwise fixed [‘Noninner automorphisms of order 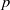$p$ of finite 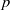$p$-groups’, J. Algebra 250 (2002), 283–287].

Keywords

finite p-groupsautomorphismsnoninner automorphisms

MSC classification

Secondary: 20D15: Nilpotent groups, $p$-groups

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 89 , Issue 2 , April 2014 , pp. 202 - 209
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Abdollahi, A., ‘Powerful $p$-groups have noninner automorphisms of order $p$ and some cohomology’, J. Algebra 323 (2010), 779–789.CrossRefGoogle Scholar
Abdollahi, A., ‘Finite $p$-groups of class 2 have noninner automorphisms of order $p$’, J. Algebra 312 (2007), 876–879.Google Scholar
Abdollahi, A., Ghoraishi, M. and Wilkens, B., ‘Finite $p$-groups of class 3 have noninner automorphisms of order $p$’, Beiträge Algebra Geom. 54 (1) (2013), 363–381.Google Scholar
Dekimpe, K. and Eick, B., ‘Computational aspects of group extensions and thier application in topology’, Exp. Math. 11 (2) (2002), 183–200.Google Scholar
Deaconescu, M. and Silberberg, G., ‘Noninner automorphisms of order $p$ of finite $p$-groups’, J. Algebra 250 (2002), 283–287.CrossRefGoogle Scholar
The GAP group, GAP-Groups, Algorithms, and Programming, version 4.4.12, www.gap-system.org (2008).Google Scholar
Gaschütz, W., ‘Nichtabelsche $p$-Gruppen besitzen äussere $p$-Automorphismen’, J. Algebra 4 (1966), 1–2.Google Scholar
Gorenstein, D., Finite Groups (Harper & Row, New York, 1968).Google Scholar
Ghoraishi, S. M., ‘A note on automorphisms of finite $p$-groups’, Bull. Aust. Math. Soc. 87 (2013), 24–26.Google Scholar
Jamalli, A. R. and Viseh, M., ‘On the existence of noinner automorphisms of order two in finite 2-groups’, Bull. Aust. Math. Soc. 87 (2013), 278–287.Google Scholar
Liebeck, H., ‘Outer automorphisms in nilpotent $p$-groups of class 2’, J. Lond. Math. Soc. 40 (1965), 268–275.Google Scholar
Mazurov, V. D. and Khukhro (eds), E. I., Unsolved Problems in Group Theory, The Kourovka Notebook, 16 (Russian Academy of Sciences, Siberian Division, Institue of Mathematics, Novosibirisk, 2006).Google Scholar
Schmid, P., ‘A cohomological property of regular $p$-groups’, Math. Z. 175 (1980), 1–3.Google Scholar
Shabani-Attar, M., ‘Existence of noninner automorphisms of order $p$ in some finite $p$-groups’, Bull. Aust. Math. Soc. 87 (2013), 272–277.CrossRefGoogle Scholar
Sims, C. C., Computation with Finitely Presented Groups (Cambridge University Press, Cambridge, 1994).CrossRefGoogle Scholar