No CrossRef data available.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 30 August 2018
Let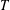 
$T$ be a finite simple group of Lie type in characteristic 
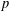$p$, and let 
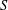$S$ be a Sylow subgroup of 
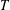$T$ with maximal order. It is well known that 
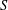$S$ is a Sylow 
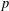$p$-subgroup except for an explicit list of exceptions and that 
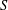$S$ is always ‘large’ in the sense that 
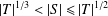$|T|^{1/3}<|S|\leq |T|^{1/2}$. One might anticipate that, moreover, the Sylow 
$r$-subgroups of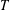 
$T$ with 
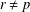$r\neq p$ are usually significantly smaller than 
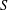$S$. We verify this hypothesis by proving that, for every 
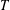$T$ and every prime divisor 
$r$ of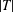 
$|T|$ with 
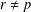$r\neq p$, the order of the Sylow 
$r$-subgroup of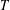 
$T$ is at most 
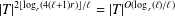$|T|^{2\lfloor \log _{r}(4(\ell +1)r)\rfloor /\ell }=|T|^{O(\log _{r}(\ell )/\ell )}$, where 
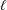$\ell$ is the Lie rank of 
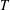$T$.
The authors acknowledge support from the Australian Research Council (ARC) grant DP140100416 and the first author also acknowledges support from DP160102323; the first and third authors are grateful to RWTH Aachen University for financial support and hospitality during their respective visits in 2017, when the research leading to this paper was undertaken.
You have
Access