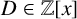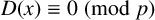1 Introduction
Let P be a univariate polynomial with integer coefficients. A prime p is said to be a prime divisor of P if p divides
![]() $P(n)$
for some integer n. Denote the set of prime divisors of P by
$P(n)$
for some integer n. Denote the set of prime divisors of P by
![]() $S(P)$
.
$S(P)$
.
Consider the structure of the sets
![]() $S(P)$
. One may easily prove, by elementary means, that
$S(P)$
. One may easily prove, by elementary means, that
![]() $S(P)$
is infinite when P is nonconstant. The Chebotarev density theorem proves that
$S(P)$
is infinite when P is nonconstant. The Chebotarev density theorem proves that
![]() $S(P)$
in fact has positive density in the set of primes (again when P is nonconstant). However, no simple description of the set
$S(P)$
in fact has positive density in the set of primes (again when P is nonconstant). However, no simple description of the set
![]() $S(P)$
is known in the general case, though quadratic reciprocity yields a characterisation in the case
$S(P)$
is known in the general case, though quadratic reciprocity yields a characterisation in the case
![]() $\deg (P) = 2$
.
$\deg (P) = 2$
.
One may further ask what one can say about finite intersections
![]() $S(P_1) \cap \cdots \cap S(P_n)$
. Again, Chebotarev’s theorem shows that such sets have positive density. Nagell [Reference Nagell3] has given a more elementary argument proving the infinitude of
$S(P_1) \cap \cdots \cap S(P_n)$
. Again, Chebotarev’s theorem shows that such sets have positive density. Nagell [Reference Nagell3] has given a more elementary argument proving the infinitude of
![]() $S(P_1) \cap S(P_2)$
. A somewhat easier proof can be found in [Reference Gerst and Brillhart2, Theorem 7].
$S(P_1) \cap S(P_2)$
. A somewhat easier proof can be found in [Reference Gerst and Brillhart2, Theorem 7].
It turns out that such intersections are again of the form
![]() $S(D)$
for some
$S(D)$
for some
![]() $D \in \mathbb {Z}[x]$
.
$D \in \mathbb {Z}[x]$
.
Theorem 1.1. Let
![]() $A, B \in \mathbb {Z}[x]$
be nonconstant. There exists a nonconstant polynomial
$A, B \in \mathbb {Z}[x]$
be nonconstant. There exists a nonconstant polynomial
![]() $D \in \mathbb {Z}[x]$
such that
$D \in \mathbb {Z}[x]$
such that
![]() $S(A) \cap S(B) = S(D).$
$S(A) \cap S(B) = S(D).$
Let F be a system of polynomial equations with integer coefficients in finitely many variables. Ax [Reference Ax1] proved that the set
![]() $S(F)$
of primes p such that F is solvable modulo p may be written as a finite combination of unions, intersections and complements of sets of the form
$S(F)$
of primes p such that F is solvable modulo p may be written as a finite combination of unions, intersections and complements of sets of the form
![]() $S(P)$
with
$S(P)$
with
![]() $P \in \mathbb {Z}[x]$
. This has been improved by van den Dries [Reference van den Dries4]: one may write
$P \in \mathbb {Z}[x]$
. This has been improved by van den Dries [Reference van den Dries4]: one may write
![]() $S(F)$
as a finite intersection of sets
$S(F)$
as a finite intersection of sets
![]() $S(P)$
. Combining this with Theorem 1.1 immediately gives the following result.
$S(P)$
. Combining this with Theorem 1.1 immediately gives the following result.
Theorem 1.2. Let
![]() $F_1, \ldots , F_m \in \mathbb {Z}[x_1, \ldots , x_n]$
be arbitrary. There exists a polynomial
$F_1, \ldots , F_m \in \mathbb {Z}[x_1, \ldots , x_n]$
be arbitrary. There exists a polynomial
![]() $D \in \mathbb {Z}[x]$
such that for any prime p, the system of equations
$D \in \mathbb {Z}[x]$
such that for any prime p, the system of equations
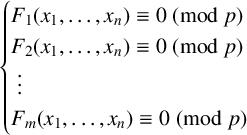 $$ \begin{align*} \begin{cases} F_1(x_1, \ldots , x_n) \equiv 0 \pmod{p} \\ F_2(x_1, \ldots , x_n) \equiv 0 \pmod{p} \\ \ \vdots \\ F_m(x_1, \ldots , x_n) \equiv 0 \pmod{p} \\ \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} F_1(x_1, \ldots , x_n) \equiv 0 \pmod{p} \\ F_2(x_1, \ldots , x_n) \equiv 0 \pmod{p} \\ \ \vdots \\ F_m(x_1, \ldots , x_n) \equiv 0 \pmod{p} \\ \end{cases} \end{align*} $$
is solvable if and only if
![]() $p \in S(D)$
.
$p \in S(D)$
.
Clearly, if there are some
![]() $G_1, \ldots , G_m \in \mathbb {Z}[x_1, \ldots , x_n]$
such that
$G_1, \ldots , G_m \in \mathbb {Z}[x_1, \ldots , x_n]$
such that
![]() $F_1G_1 + \cdots + F_mG_m$
is a nonzero constant, then there are only finitely many primes p with
$F_1G_1 + \cdots + F_mG_m$
is a nonzero constant, then there are only finitely many primes p with
![]() $F_1 \equiv \cdots \equiv F_m \equiv 0 \pmod {p}$
solvable. By the Nullstellensatz, this is equivalent to the assertion that the system
$F_1 \equiv \cdots \equiv F_m \equiv 0 \pmod {p}$
solvable. By the Nullstellensatz, this is equivalent to the assertion that the system
![]() $F_1 = \cdots = F_m = 0$
has no complex solutions. In any other case, there are infinitely many such p [Reference van den Dries4, Proposition 2.7] and D in Theorem 1.2 is nonconstant.
$F_1 = \cdots = F_m = 0$
has no complex solutions. In any other case, there are infinitely many such p [Reference van den Dries4, Proposition 2.7] and D in Theorem 1.2 is nonconstant.
It seems that the results above are known to experts. However, it is relatively difficult to find references for the results, especially if one wishes to find elementary treatments. A proof of Theorem 1.2 (using algebraic geometric language) may be found in [Reference van Dobben de Bruyn5]. An elementary exposition, which falls a little short of Theorem 1.1, is given in [Reference Gerst and Brillhart2] (in particular Theorem 11 there).
The purpose of this note is to give a short, self-contained and elementary proof of Theorem 1.1. Our approach is not far from the ideas of [Reference Gerst and Brillhart2]. The proof is constructive, allowing one to take
![]() $\deg (D) \le \deg (A)\deg (B)$
. This is optimal in the general case (see the remarks after the proof).
$\deg (D) \le \deg (A)\deg (B)$
. This is optimal in the general case (see the remarks after the proof).
The result of Theorem 1.2 is considerably more difficult: one needs some version of the Lang–Weil bound to deduce that ‘generic’ systems with
![]() $m < n$
are solvable modulo p for p large enough, and such results are not easy to prove.
$m < n$
are solvable modulo p for p large enough, and such results are not easy to prove.
2 Proof of Theorem 1.1
We begin by proving that to obtain Theorem 1.1, it suffices to show that for any monic
![]() $A, B \in \mathbb {Z}[x]$
, there exists
$A, B \in \mathbb {Z}[x]$
, there exists
![]() $D \in \mathbb {Z}[x]$
such that
$D \in \mathbb {Z}[x]$
such that
![]() $S(A) \cap S(B)$
and
$S(A) \cap S(B)$
and
![]() $S(D)$
differ by only finitely many primes. This follows from the following two lemmas.
$S(D)$
differ by only finitely many primes. This follows from the following two lemmas.
Lemma 2.1. Let
![]() $P \in \mathbb {Z}[x]$
and p be given. There exist polynomials
$P \in \mathbb {Z}[x]$
and p be given. There exist polynomials
![]() $P_+, P_- \in \mathbb {Z}[x]$
such that
$P_+, P_- \in \mathbb {Z}[x]$
such that
![]() $S(P_+) = S(P) \cup \{p\}$
and
$S(P_+) = S(P) \cup \{p\}$
and
![]() $S(P_-) = S(P) \setminus \{p\}$
.
$S(P_-) = S(P) \setminus \{p\}$
.
Proof. Take
![]() $P_+(x) = pP(x)$
. If
$P_+(x) = pP(x)$
. If
![]() $P(0) = 0$
, take
$P(0) = 0$
, take
![]() $P_-(x) = px + 1$
. Otherwise, let
$P_-(x) = px + 1$
. Otherwise, let
![]() $P_-(x) = P(p^{k+1}x)/p^k$
, where
$P_-(x) = P(p^{k+1}x)/p^k$
, where
![]() $p^k$
is the largest power of p dividing
$p^k$
is the largest power of p dividing
![]() $P(0)$
. One easily checks that this works.
$P(0)$
. One easily checks that this works.
Lemma 2.2. Let
![]() $P \in \mathbb {Z}[x]$
be given. There exists a monic polynomial
$P \in \mathbb {Z}[x]$
be given. There exists a monic polynomial
![]() $Q \in \mathbb {Z}[x]$
such that
$Q \in \mathbb {Z}[x]$
such that
![]() $S(P)$
and
$S(P)$
and
![]() $S(Q)$
differ by only finitely many elements.
$S(Q)$
differ by only finitely many elements.
Proof. Let c be the leading coefficient of P. One easily checks that the polynomial
![]() $Q(x) = c^{\deg (P) - 1}P(x/c)$
works.
$Q(x) = c^{\deg (P) - 1}P(x/c)$
works.
We make the further reduction that A and B may be assumed to be irreducible. Assume we have proven Theorem 1.1 for irreducible and monic
![]() $A, B$
. Now, by Gauss’s lemma, write
$A, B$
. Now, by Gauss’s lemma, write
![]() $A = A_1 \cdots A_a$
and
$A = A_1 \cdots A_a$
and
![]() $B = B_1 \cdots B_b$
, where
$B = B_1 \cdots B_b$
, where
![]() $A_i, B_j \in \mathbb {Z}[x]$
are irreducible and monic. Let
$A_i, B_j \in \mathbb {Z}[x]$
are irreducible and monic. Let
![]() $D_{i, j} \in \mathbb {Z}[x]$
be such that
$D_{i, j} \in \mathbb {Z}[x]$
be such that
![]() $S(A_i) \cap S(B_j) = S(D_{i, j})$
. Then
$S(A_i) \cap S(B_j) = S(D_{i, j})$
. Then
![]() $S(A) \cap S(B) = S(D)$
, where D is the product of all the
$S(A) \cap S(B) = S(D)$
, where D is the product of all the
![]() $D_{i, j}$
.
$D_{i, j}$
.
Hence, assume A and B are monic and irreducible. Fix any root
![]() $\alpha $
of A. As usual, denote by
$\alpha $
of A. As usual, denote by
![]() $\mathbb {Z}/p\mathbb {Z}$
the integers modulo p and let
$\mathbb {Z}/p\mathbb {Z}$
the integers modulo p and let
![]() $\mathbb {Z}[\alpha ] = \{P(\alpha ) \mid P \in \mathbb {Z}[x]\}$
.
$\mathbb {Z}[\alpha ] = \{P(\alpha ) \mid P \in \mathbb {Z}[x]\}$
.
Lemma 2.3. Let
![]() $p \in S(A)$
be a prime and let a be an integer such that
$p \in S(A)$
be a prime and let a be an integer such that
![]() $A(a) = 0$
. There exists a homomorphism
$A(a) = 0$
. There exists a homomorphism
![]() $\varphi : \mathbb {Z}[\alpha ] \to \mathbb {Z}/p\mathbb {Z}$
with
$\varphi : \mathbb {Z}[\alpha ] \to \mathbb {Z}/p\mathbb {Z}$
with
![]() $\varphi (\alpha ) \equiv a \pmod {p}$
.
$\varphi (\alpha ) \equiv a \pmod {p}$
.
Proof. For
![]() $\beta \in \mathbb {Z}[\alpha ]$
, write
$\beta \in \mathbb {Z}[\alpha ]$
, write
![]() $\beta = P(\alpha ), P \in \mathbb {Z}[x]$
, and define
$\beta = P(\alpha ), P \in \mathbb {Z}[x]$
, and define
![]() $\varphi (\beta ) \equiv P(a) \pmod {p}$
. This is well defined, since if
$\varphi (\beta ) \equiv P(a) \pmod {p}$
. This is well defined, since if
![]() $\beta = P_1(\alpha ) = P_2(\alpha )$
, then
$\beta = P_1(\alpha ) = P_2(\alpha )$
, then
![]() $P_1 - P_2$
has
$P_1 - P_2$
has
![]() $\alpha $
as its root and thus is divisible by the minimal polynomial A, resulting in
$\alpha $
as its root and thus is divisible by the minimal polynomial A, resulting in
![]() $P_1(a) \equiv P_2(a) \pmod {p}$
. Clearly,
$P_1(a) \equiv P_2(a) \pmod {p}$
. Clearly,
![]() $\varphi $
is a homomorphism with
$\varphi $
is a homomorphism with
![]() $\varphi (\alpha ) \equiv a \pmod {p}$
.
$\varphi (\alpha ) \equiv a \pmod {p}$
.
Factorise B in
![]() $\mathbb {Q}(\alpha )[x]$
into a product
$\mathbb {Q}(\alpha )[x]$
into a product
![]() $E_1E_2 \cdots E_t$
of irreducibles. By Gauss’s lemma, we may take the coefficients of
$E_1E_2 \cdots E_t$
of irreducibles. By Gauss’s lemma, we may take the coefficients of
![]() $E_i$
to lie in
$E_i$
to lie in
![]() $\mathbb {Z}[\alpha ]$
. Let
$\mathbb {Z}[\alpha ]$
. Let
![]() $\beta _1, \ldots , \beta _t$
be some roots of
$\beta _1, \ldots , \beta _t$
be some roots of
![]() $E_1, \ldots , E_t$
. By the primitive element theorem, let
$E_1, \ldots , E_t$
. By the primitive element theorem, let
![]() $G_1, \ldots , G_t \in \mathbb {Z}[x, y]$
be such that
$G_1, \ldots , G_t \in \mathbb {Z}[x, y]$
be such that
![]() $\mathbb {Q}(\alpha , \beta _i) = \mathbb {Q}(G_i(\alpha , \beta _i))$
. (One may take
$\mathbb {Q}(\alpha , \beta _i) = \mathbb {Q}(G_i(\alpha , \beta _i))$
. (One may take
![]() $G_i(x, y) = x + n_iy$
for some suitable
$G_i(x, y) = x + n_iy$
for some suitable
![]() $n_i \in \mathbb {Z}$
.) Let
$n_i \in \mathbb {Z}$
.) Let
![]() $D_i$
be the minimal polynomial of
$D_i$
be the minimal polynomial of
![]() $G_i(\alpha , \beta _i)$
and let
$G_i(\alpha , \beta _i)$
and let
We show that
![]() $S(A) \cap S(B)$
and
$S(A) \cap S(B)$
and
![]() $S(D)$
differ by only finitely many primes, which proves the theorem. This is done in the following two lemmas.
$S(D)$
differ by only finitely many primes, which proves the theorem. This is done in the following two lemmas.
Lemma 2.4. We have
![]() $S(A) \cap S(B) \subset S(D) \cup T$
for some finite set T.
$S(A) \cap S(B) \subset S(D) \cup T$
for some finite set T.
Proof. For each i, define
![]() $D_i^{\ast }(x) = D_i(G_i(\alpha , x))$
. Hence,
$D_i^{\ast }(x) = D_i(G_i(\alpha , x))$
. Hence,
![]() $D_i^{\ast } \in \mathbb {Z}[\alpha ][x]$
has
$D_i^{\ast } \in \mathbb {Z}[\alpha ][x]$
has
![]() $\beta _i$
as its root, so
$\beta _i$
as its root, so
![]() $D_i^{\ast }$
is divisible by
$D_i^{\ast }$
is divisible by
![]() $E_i$
. Write
$E_i$
. Write
![]() $D_i^{\ast } = E_iF_i$
, where the coefficients of
$D_i^{\ast } = E_iF_i$
, where the coefficients of
![]() $F_i$
are polynomials in
$F_i$
are polynomials in
![]() $\alpha $
with rational coefficients. Let
$\alpha $
with rational coefficients. Let
![]() $c \in \mathbb {Z}_+$
be such that
$c \in \mathbb {Z}_+$
be such that
![]() $cF_i \in \mathbb {Z}[\alpha ][x]$
for all i.
$cF_i \in \mathbb {Z}[\alpha ][x]$
for all i.
Assume
![]() $p \in S(A) \cap S(B)$
does not divide c. Let
$p \in S(A) \cap S(B)$
does not divide c. Let
![]() $a, b \in \mathbb {Z}$
be such that
$a, b \in \mathbb {Z}$
be such that
![]() $A(a) \equiv B(b) \equiv 0 \pmod {p}$
, and let
$A(a) \equiv B(b) \equiv 0 \pmod {p}$
, and let
![]() $\varphi $
be as in Lemma 2.3. Then modulo p,
$\varphi $
be as in Lemma 2.3. Then modulo p,
Let i be such that
![]() $\varphi (E_i(b)) \equiv 0 \pmod {p}$
. Now,
$\varphi (E_i(b)) \equiv 0 \pmod {p}$
. Now,
and hence
![]() $p \in S(D_i) \subset S(D)$
.
$p \in S(D_i) \subset S(D)$
.
Lemma 2.5. We have
![]() $S(D) \subset (S(A) \cap S(B)) \cup T$
for some finite set T.
$S(D) \subset (S(A) \cap S(B)) \cup T$
for some finite set T.
Proof. The argument is relatively standard (see, for example, [Reference Gerst and Brillhart2, Theorem 2]).
It suffices to show that for any i and any large enough prime
![]() $p \in S(D_i)$
, we have
$p \in S(D_i)$
, we have
![]() $p \in S(A) \cap S(B)$
. We show that
$p \in S(A) \cap S(B)$
. We show that
![]() $p \in S(A)$
for large
$p \in S(A)$
for large
![]() $p \in S(D_i)$
. The proof for B is similar. Let
$p \in S(D_i)$
. The proof for B is similar. Let
![]() $\gamma _i = G_i(\alpha , \beta _i)$
. By the choice of
$\gamma _i = G_i(\alpha , \beta _i)$
. By the choice of
![]() $G_i$
, there exists
$G_i$
, there exists
![]() $P \in \mathbb {Q}[x]$
such that
$P \in \mathbb {Q}[x]$
such that
![]() $P(\gamma _i) = \alpha $
. Now
$P(\gamma _i) = \alpha $
. Now
![]() $A(P(\gamma _i)) = 0$
, so we may write
$A(P(\gamma _i)) = 0$
, so we may write
![]() $A(P(x)) = D_i(x)Q(x)$
for
$A(P(x)) = D_i(x)Q(x)$
for
![]() $Q \in \mathbb {Q}[x]$
. Let
$Q \in \mathbb {Q}[x]$
. Let
![]() $c \in \mathbb {Z}_+$
be such that
$c \in \mathbb {Z}_+$
be such that
![]() $cQ \in \mathbb {Z}[x]$
.
$cQ \in \mathbb {Z}[x]$
.
Assume that
![]() $p \in S(D_i)$
does not divide c nor the denominator of any coefficient of P. Let
$p \in S(D_i)$
does not divide c nor the denominator of any coefficient of P. Let
![]() $d \in \mathbb {Z}$
be such that
$d \in \mathbb {Z}$
be such that
![]() $D_i(d) \equiv 0 \pmod {p}$
. Then
$D_i(d) \equiv 0 \pmod {p}$
. Then
![]() $cA(P(d)) = D_i(d) \cdot cQ(d) \equiv 0 \pmod {p}$
. Hence, there is a rational number
$cA(P(d)) = D_i(d) \cdot cQ(d) \equiv 0 \pmod {p}$
. Hence, there is a rational number
![]() $P(d) = r/s$
with
$P(d) = r/s$
with
![]() $p \nmid s$
such that
$p \nmid s$
such that
![]() $cA(r/s)$
is an integer divisible by p. A calculation reveals that
$cA(r/s)$
is an integer divisible by p. A calculation reveals that
![]() $cA(rs^{p-2})$
is divisible by p, corresponding to the fact that
$cA(rs^{p-2})$
is divisible by p, corresponding to the fact that
![]() $r/s$
may be interpreted modulo p as
$r/s$
may be interpreted modulo p as
![]() $rs^{p-2} \pmod {p}$
(by Fermat’s little theorem), and therefore
$rs^{p-2} \pmod {p}$
(by Fermat’s little theorem), and therefore
![]() $p \in S(A)$
.
$p \in S(A)$
.
Remark 2.6. An easy calculation shows the constructed D has degree
![]() $\deg (A)\deg (B)$
.
$\deg (A)\deg (B)$
.
Remark 2.7. There are A and B such that any D with
![]() $S(A) \cap S(B) = S(D)$
satisfies
$S(A) \cap S(B) = S(D)$
satisfies
![]() $\deg (D) \ge \deg (A)\deg (B)$
. By the Chebotarev density theorem, the density of
$\deg (D) \ge \deg (A)\deg (B)$
. By the Chebotarev density theorem, the density of
![]() $S(P)$
is at least
$S(P)$
is at least
![]() $1/\deg (P)$
for any nonconstant
$1/\deg (P)$
for any nonconstant
![]() $P \in \mathbb {Z}[x]$
. If A and B are such that
$P \in \mathbb {Z}[x]$
. If A and B are such that
![]() $S(A) \cap S(B)$
has density
$S(A) \cap S(B)$
has density
![]() $1/\deg (A)\deg (B)$
(take A and B to be, for example, the nth and mth cyclotomic polynomials for
$1/\deg (A)\deg (B)$
(take A and B to be, for example, the nth and mth cyclotomic polynomials for
![]() $(n, m) = 1$
), then
$(n, m) = 1$
), then
![]() $S(A) \cap S(B) = S(D)$
implies
$S(A) \cap S(B) = S(D)$
implies
![]() $\deg (D) \ge \deg (A)\deg (B)$
.
$\deg (D) \ge \deg (A)\deg (B)$
.
Remark 2.8. Combining the results of the previous remarks shows that the density of
![]() $S(P_1) \cap \cdots \cap S(P_n)$
is at least
$S(P_1) \cap \cdots \cap S(P_n)$
is at least
![]() $1/\deg (P_1) \cdots \deg (P_n)$
for nonconstant
$1/\deg (P_1) \cdots \deg (P_n)$
for nonconstant
![]() $P_i$
. Some equality cases are given by quadratic or cyclotomic polynomials.
$P_i$
. Some equality cases are given by quadratic or cyclotomic polynomials.
Remark 2.9. With slightly more care, one can prove the following strengthening of Theorem 1.1: for any
![]() $A, B$
, there exists D such that
$A, B$
, there exists D such that
![]() $A(x) \equiv B(y) \equiv 0 \pmod {m}$
is solvable if and only if
$A(x) \equiv B(y) \equiv 0 \pmod {m}$
is solvable if and only if
![]() $D(z) \equiv 0 \pmod {m}$
, where the modulus m is not necessarily a prime. (One needs the following consequence of Hensel’s lemma: if
$D(z) \equiv 0 \pmod {m}$
, where the modulus m is not necessarily a prime. (One needs the following consequence of Hensel’s lemma: if
![]() $P \in \mathbb {Z}[x]$
is given, for all but finitely many primes
$P \in \mathbb {Z}[x]$
is given, for all but finitely many primes
![]() $p \in S(P)$
, the equation
$p \in S(P)$
, the equation
![]() $P(x) \equiv 0 \pmod {p^k}$
is solvable for any
$P(x) \equiv 0 \pmod {p^k}$
is solvable for any
![]() $k \in \mathbb {Z}_+$
.)
$k \in \mathbb {Z}_+$
.)