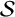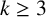1 Introduction
We denote
![]() $\mathbb {N}=\{0,1,2,\ldots \}$
and we define a numerical semigroup to be a set
$\mathbb {N}=\{0,1,2,\ldots \}$
and we define a numerical semigroup to be a set
![]() $\mathcal {S}\subseteq \mathbb {N}$
that is closed under addition and contains 0. A numerical semigroup can be defined by a set of generators,
$\mathcal {S}\subseteq \mathbb {N}$
that is closed under addition and contains 0. A numerical semigroup can be defined by a set of generators,
and if
![]() $a_1,\ldots ,a_n$
are the minimal set of generators of
$a_1,\ldots ,a_n$
are the minimal set of generators of
![]() $\mathcal {S}$
, we say that
$\mathcal {S}$
, we say that
![]() $\mathcal {S}$
has embedding dimension
$\mathcal {S}$
has embedding dimension
![]() $\mathsf e(\mathcal {S}) = n$
. For example,
$\mathsf e(\mathcal {S}) = n$
. For example,
has embedding dimension 2.
If
![]() $\mathcal {S}$
is a numerical semigroup, then an interesting way to create a new numerical semigroup is by taking the quotient
$\mathcal {S}$
is a numerical semigroup, then an interesting way to create a new numerical semigroup is by taking the quotient
by some positive integer d. Note that
![]() $\mathcal {S}/d$
is itself a numerical semigroup, one that in particular satisfies
$\mathcal {S}/d$
is itself a numerical semigroup, one that in particular satisfies
![]() $\mathcal {S} \subseteq \mathcal {S}/d \subseteq \mathbb {N}$
. For example,
$\mathcal {S} \subseteq \mathcal {S}/d \subseteq \mathbb {N}$
. For example,
Quotients of numerical semigroups have appeared in the literature over the past couple of decades [Reference Rosales and García-Sánchez17, Reference Rosales21] as well as recently [Reference Adeniran, Butler, Defant, Gao, Harris, Hettle, Liang, Nam and Volk1, Reference Moscariello14]. See [Reference Rosales and García-Sánchez18, Ch. 5] for a thorough overview.
Definition 1.1. We say a numerical semigroup
![]() $\mathcal {S}$
is a k-quotient if
$\mathcal {S}$
is a k-quotient if
![]() $\mathcal {S}=\langle a_1,\ldots ,a_k\rangle /d$
for some positive integers
$\mathcal {S}=\langle a_1,\ldots ,a_k\rangle /d$
for some positive integers
![]() $d, a_1, \ldots , a_k$
. The quotient rank of
$d, a_1, \ldots , a_k$
. The quotient rank of
![]() $\mathcal {S}$
is the smallest k such that
$\mathcal {S}$
is the smallest k such that
![]() $\mathcal {S}$
is a k-quotient, and we say
$\mathcal {S}$
is a k-quotient, and we say
![]() $\mathcal {S}$
has full quotient rank if its quotient rank is
$\mathcal {S}$
has full quotient rank if its quotient rank is
![]() $\mathsf e(\mathcal {S})$
(since
$\mathsf e(\mathcal {S})$
(since
![]() $\mathcal {S}={\mathcal {S}}/{1}$
, its quotient rank is at most
$\mathcal {S}={\mathcal {S}}/{1}$
, its quotient rank is at most
![]() $\mathsf e(S)$
).
$\mathsf e(S)$
).
Numerical semigroups of quotient rank 2 are precisely the proportionally modular numerical semigroups [Reference Rosales and Urbano-Blanco22], which have been well studied [Reference Bullejos and Rosales6, Reference Rosales, García-Sánchez, García-García and Urbano-Blanco20]. This includes arithmetical numerical semigroups (whose generators have the form
![]() $a, a + d, \ldots , a + kd$
with
$a, a + d, \ldots , a + kd$
with
![]() $\gcd (a,d) = 1$
), which have a rich history in the numerical semigroup literature [Reference Alfonsín2, Reference Amos, Chapman, Hine and Paixão4, Reference Gimenez, Sengupta and Srinivasan9]. In fact, generalised arithmetical numerical semigroups [Reference Omidali and Rahmati16], whose generating sets have the form
$\gcd (a,d) = 1$
), which have a rich history in the numerical semigroup literature [Reference Alfonsín2, Reference Amos, Chapman, Hine and Paixão4, Reference Gimenez, Sengupta and Srinivasan9]. In fact, generalised arithmetical numerical semigroups [Reference Omidali and Rahmati16], whose generating sets have the form
![]() $a, ah + d, \ldots , ah + kd$
, can also be shown to have quotient rank 3.
$a, ah + d, \ldots , ah + kd$
, can also be shown to have quotient rank 3.
For quotient rank
![]() $k \ge 3$
, much less is known. It is identified as an open problem in [Reference Delgado, García-Sánchez and Rosales8] that no numerical semigroup has been proven to have quotient rank at least 4. Since then, the only progress in this direction is [Reference Moreno, Nicola, Pardo and Thomas13], wherein it is shown that there exist infinitely many numerical semigroups with quotient rank at least 4, though no explicit examples are given.
$k \ge 3$
, much less is known. It is identified as an open problem in [Reference Delgado, García-Sánchez and Rosales8] that no numerical semigroup has been proven to have quotient rank at least 4. Since then, the only progress in this direction is [Reference Moreno, Nicola, Pardo and Thomas13], wherein it is shown that there exist infinitely many numerical semigroups with quotient rank at least 4, though no explicit examples are given.
With this in mind, we state the main question of the present paper.
Main Problem. When is a given numerical semigroup
![]() $\mathcal {S}$
a k-quotient?
$\mathcal {S}$
a k-quotient?
Our main structural results, which are stated in Section 2, are as follows.
-
• We prove a sufficient condition for full quotient rank (Theorem 2.1), which we use to obtain, for each k, a numerical semigroup of embedding dimension
 $k + 1$
that is not a k-quotient (Theorem 3.1). When
$k + 1$
that is not a k-quotient (Theorem 3.1). When
 $k \ge 3$
, this is the first known example of a numerical semigroup that is not a k-quotient. We also construct, for each k, a numerical semigroup that cannot be written as an intersection of k-quotients (Theorem 3.2), settling a conjecture posed in [Reference Moreno, Nicola, Pardo and Thomas13].
$k \ge 3$
, this is the first known example of a numerical semigroup that is not a k-quotient. We also construct, for each k, a numerical semigroup that cannot be written as an intersection of k-quotients (Theorem 3.2), settling a conjecture posed in [Reference Moreno, Nicola, Pardo and Thomas13]. -
• We prove quotient rank is sub-additive whenever the denominators are coprime. This provides a new method of proving a given numerical semigroup is a quotient: partition its generating set and prove that each subset generates a quotient, for example,
We use this result to prove that any numerical semgiroup with maximal embedding dimension (that is, the smallest generator equals the embedding dimension) fails to have full quotient rank (Theorem 4.5). $$ \begin{align*} \langle 11,12,13,17,18,19,20 \rangle &= \langle 11,12,13 \rangle + \langle 17,18,19,20 \rangle = \frac{\langle 11,13\rangle}{2}+\frac{\langle 17,20\rangle}{3} \\ &= \frac{3\langle 11,13\rangle + 2\langle 17,20\rangle}{2 \cdot 3} = \frac{\langle 33,34,39,40\rangle}{6}. \end{align*} $$
$$ \begin{align*} \langle 11,12,13,17,18,19,20 \rangle &= \langle 11,12,13 \rangle + \langle 17,18,19,20 \rangle = \frac{\langle 11,13\rangle}{2}+\frac{\langle 17,20\rangle}{3} \\ &= \frac{3\langle 11,13\rangle + 2\langle 17,20\rangle}{2 \cdot 3} = \frac{\langle 33,34,39,40\rangle}{6}. \end{align*} $$
Our remaining results are probabilistic in nature. We examine two well-studied models for ‘randomly selecting’ a numerical semigroup: the ‘box’ model, where the number of generators and a bound on the generators are fixed [Reference Aliev, Henk and Hinrichs3, Reference Arnol’d5, Reference Burgeĭn and Sinaĭ7]; as well as a model where the smallest generator and the number of gaps are fixed [Reference Kaplan10], whose prior study has yielded connections to enumerative combinatorics [Reference Rosales, García-Sánchez, García-García and Branco19] and polyhedral geometry [Reference Kaplan and O’Neill11, Reference Kunz12]. We prove that under the first model, asymptotically all semigroups have full quotient rank (Theorem 4.1), while under the second model, asymptotically no semigroups have full quotient rank (Theorem 4.5).
Our results also represent partial progress on the following question, which has proved difficult.
Problem 1.2. Given a numerical semigroup
![]() $\mathcal {S}$
and a positive number k, is there an algorithm to determine whether
$\mathcal {S}$
and a positive number k, is there an algorithm to determine whether
![]() $\mathcal {S}$
is a k-quotient?
$\mathcal {S}$
is a k-quotient?
Remark 1.3. Some texts require that the generators of a numerical semigroup be relatively prime, so that
![]() $\mathbb {N}\setminus \mathcal {S}$
is finite. This assumption is harmless, since any numerical semigroup can be written as
$\mathbb {N}\setminus \mathcal {S}$
is finite. This assumption is harmless, since any numerical semigroup can be written as
![]() $m\mathcal {S}$
, where the generators of
$m\mathcal {S}$
, where the generators of
![]() $\mathcal {S}$
are relatively prime, and it does not affect k-quotientability: given a positive integer d, one can readily check that
$\mathcal {S}$
are relatively prime, and it does not affect k-quotientability: given a positive integer d, one can readily check that
where
![]() $m' = m/\gcd (m,d)$
and
$m' = m/\gcd (m,d)$
and
![]() $d' = d/\gcd (m,d)$
.
$d' = d/\gcd (m,d)$
.
2 When is
 $\mathcal {S}$
not a k-quotient?
$\mathcal {S}$
not a k-quotient?
In this section, we give two structural results. The first (Theorem 2.1) is a necessary condition for a given numerical semigroup
![]() $\mathcal {S}$
to be a k-quotient, which forms the backbone of the constructions in Section 3 and the probabilistic results in Section 4. The second (Theorem 2.3) is a constructive proof that quotient rank is sub-additive, provided the denominators are relatively prime.
$\mathcal {S}$
to be a k-quotient, which forms the backbone of the constructions in Section 3 and the probabilistic results in Section 4. The second (Theorem 2.3) is a constructive proof that quotient rank is sub-additive, provided the denominators are relatively prime.
In what follows, we write
![]() $[p] = \{1,2,\ldots ,p\}$
for any positive integer p, and given a collection of vectors
$[p] = \{1,2,\ldots ,p\}$
for any positive integer p, and given a collection of vectors
![]() $\{\mathbf{v}_i\}$
and a set of indices I, we define
$\{\mathbf{v}_i\}$
and a set of indices I, we define
![]() $\mathbf{v}_I=\sum _{i\in I}\mathbf{v}_i$
.
$\mathbf{v}_I=\sum _{i\in I}\mathbf{v}_i$
.
Theorem 2.1. Suppose
for some
![]() $b_i\in \mathbb {N}$
and positive integer d. Given any elements
$b_i\in \mathbb {N}$
and positive integer d. Given any elements
![]() $s_1,\ldots ,s_p \in \mathcal {S}$
with
$s_1,\ldots ,s_p \in \mathcal {S}$
with
![]() $p> k$
, there exists a nonempty subset
$p> k$
, there exists a nonempty subset
![]() $I\subseteq [p]$
such that
$I\subseteq [p]$
such that
![]() $s_I/2\in \mathcal {S}$
.
$s_I/2\in \mathcal {S}$
.
Proof. Let
![]() $\mathbf{b}=(b_1,\ldots ,b_k)$
. For
$\mathbf{b}=(b_1,\ldots ,b_k)$
. For
![]() $1\le i\le p$
, let
$1\le i\le p$
, let
![]() $\mathbf{c}_i=(c_{i1},\ldots ,c_{ik})\in \mathbb {N}^k$
be such that
$\mathbf{c}_i=(c_{i1},\ldots ,c_{ik})\in \mathbb {N}^k$
be such that
which exist since
![]() $s_i\in \mathcal {S}$
. For a vector
$s_i\in \mathcal {S}$
. For a vector
![]() $\mathbf{v}\in \mathbb {Z}^k$
, define
$\mathbf{v}\in \mathbb {Z}^k$
, define
![]() $\mathbf{v}\bmod 2\in \mathbb {Z}_2^k$
to be the coordinate-wise reduction of
$\mathbf{v}\bmod 2\in \mathbb {Z}_2^k$
to be the coordinate-wise reduction of
![]() $\mathbf{v}$
modulo 2. For
$\mathbf{v}$
modulo 2. For
![]() $J\subseteq [p]$
, examine
$J\subseteq [p]$
, examine
![]() $\mathbf{c}_J \bmod 2$
. There are
$\mathbf{c}_J \bmod 2$
. There are
![]() $2^p$
possible J and
$2^p$
possible J and
![]() $2^k$
possible values for
$2^k$
possible values for
![]() $\mathbf{c}_J \bmod 2$
, with
$\mathbf{c}_J \bmod 2$
, with
![]() $p>k$
, so there must be two distinct
$p>k$
, so there must be two distinct
![]() $J_1$
and
$J_1$
and
![]() $J_2$
such that
$J_2$
such that
Let
![]() $I=(J_1\setminus J_2)\cup (J_2\setminus J_1)$
be their symmetric difference, which is nonempty. Then,
$I=(J_1\setminus J_2)\cup (J_2\setminus J_1)$
be their symmetric difference, which is nonempty. Then,
so
![]() $\mathbf{c}_{I}$
has even coordinates. Let
$\mathbf{c}_{I}$
has even coordinates. Let
![]() $\mathbf{c}_I = (2q_1,\ldots ,2q_k)$
where
$\mathbf{c}_I = (2q_1,\ldots ,2q_k)$
where
![]() $q_i\in \mathbb {N}$
. Then,
$q_i\in \mathbb {N}$
. Then,
 $$ \begin{align*} s_I/2&=\sum_{i\in I}(d\cdot (c_{i1}b_1+\cdots+ c_{ik}b_k))/2 = d\sum_{j=1}^kb_j\sum_{i\in I}c_{ij}/2 =d\sum_{j=1}^k q_jb_j \end{align*} $$
$$ \begin{align*} s_I/2&=\sum_{i\in I}(d\cdot (c_{i1}b_1+\cdots+ c_{ik}b_k))/2 = d\sum_{j=1}^kb_j\sum_{i\in I}c_{ij}/2 =d\sum_{j=1}^k q_jb_j \end{align*} $$
is an element of
![]() $\mathcal {S}$
, as desired.
$\mathcal {S}$
, as desired.
Corollary 2.2. Let
![]() $\mathcal {S} = \langle a_1, \ldots , a_n \rangle $
be a numerical semigroup. If
$\mathcal {S} = \langle a_1, \ldots , a_n \rangle $
be a numerical semigroup. If
![]() $\mathcal {S}$
does not have full quotient rank, then there exists
$\mathcal {S}$
does not have full quotient rank, then there exists
![]() $I \subseteq [n]$
such that
$I \subseteq [n]$
such that
Proof. By applying Theorem 2.1 to the generating set
![]() $\{a_1, \ldots , a_n\}$
, we see that
$\{a_1, \ldots , a_n\}$
, we see that
![]() $a_J/2 \in \mathcal {S}$
for some
$a_J/2 \in \mathcal {S}$
for some
![]() $J \subseteq [n]$
. So there exist
$J \subseteq [n]$
. So there exist
![]() $c_r\in \mathbb {N}$
such that
$c_r\in \mathbb {N}$
such that
 $$ \begin{align*} \sum_{j\in J} a_j=\sum_{r\in R} 2c_r a_r, \end{align*} $$
$$ \begin{align*} \sum_{j\in J} a_j=\sum_{r\in R} 2c_r a_r, \end{align*} $$
where
![]() $R=\{r: c_r>0\}$
. Letting
$R=\{r: c_r>0\}$
. Letting
![]() $I=J\setminus R$
and subtracting each
$I=J\setminus R$
and subtracting each
![]() $a_j$
with
$a_j$
with
![]() $j\in J\cap R$
from both sides, we have
$j\in J\cap R$
from both sides, we have
 $$ \begin{align*} a_I=\sum_{i\in I} a_i = \sum_{r\in J\cap R} (2c_r-1) a_r + \sum_{r\in R\setminus J}2c_r a_r \end{align*} $$
$$ \begin{align*} a_I=\sum_{i\in I} a_i = \sum_{r\in J\cap R} (2c_r-1) a_r + \sum_{r\in R\setminus J}2c_r a_r \end{align*} $$
is an element of
![]() $\langle a_j: j\notin I\rangle $
, as desired. Note that I is nonempty, as otherwise
$\langle a_j: j\notin I\rangle $
, as desired. Note that I is nonempty, as otherwise
 $$ \begin{align*} 0 = a_I = \sum_{r\in J\cap R} (2c_r-1) a_r + \sum_{r\in R\setminus J}2c_r a_r \ge \sum_{r\in J\cap R} a_r = \sum_{r\in J} a_r> 0 \end{align*} $$
$$ \begin{align*} 0 = a_I = \sum_{r\in J\cap R} (2c_r-1) a_r + \sum_{r\in R\setminus J}2c_r a_r \ge \sum_{r\in J\cap R} a_r = \sum_{r\in J} a_r> 0 \end{align*} $$
since J is nonempty, which is a contradiction.
Theorem 2.3. If
![]() $\mathcal {S}$
and
$\mathcal {S}$
and
![]() $\mathcal {T}$
are numerical semigroups and
$\mathcal {T}$
are numerical semigroups and
![]() $\gcd (c,d) = 1$
, then
$\gcd (c,d) = 1$
, then
Proof. First suppose that
![]() $x \in \mathcal {S}/c + \mathcal {T}/d$
. Then
$x \in \mathcal {S}/c + \mathcal {T}/d$
. Then
![]() $x = s+t$
, where
$x = s+t$
, where
![]() $cs \in \mathcal {S}$
and
$cs \in \mathcal {S}$
and
![]() $dt \in \mathcal {T}$
, so
$dt \in \mathcal {T}$
, so
which implies
![]() $x \in (d\mathcal {S} + c \mathcal {T})/cd$
. Note this containment does not require
$x \in (d\mathcal {S} + c \mathcal {T})/cd$
. Note this containment does not require
![]() $\gcd (c,d) = 1$
.
$\gcd (c,d) = 1$
.
However, suppose
![]() $cdx \in d \mathcal {S} + c \mathcal {T}$
, so
$cdx \in d \mathcal {S} + c \mathcal {T}$
, so
In particular,
![]() $ct = d(cx-s)$
is a multiple of d. Since c and d are relatively prime, this implies that t is a multiple of d, say
$ct = d(cx-s)$
is a multiple of d. Since c and d are relatively prime, this implies that t is a multiple of d, say
![]() $t = bd$
. Since
$t = bd$
. Since
![]() $t \in \mathcal {T}$
, we conclude that
$t \in \mathcal {T}$
, we conclude that
![]() $b \in \mathcal {T}/d$
. Similarly, we can write
$b \in \mathcal {T}/d$
. Similarly, we can write
![]() $s = ac$
for some a and so
$s = ac$
for some a and so
![]() $a \in \mathcal {S}/c$
.
$a \in \mathcal {S}/c$
.
Substituting
![]() $t=bd$
and
$t=bd$
and
![]() $s=ac$
into (2.1), we obtain
$s=ac$
into (2.1), we obtain
By cancellation, we obtain
![]() $x = a + b$
with
$x = a + b$
with
![]() $a \in \mathcal {S}/c$
and
$a \in \mathcal {S}/c$
and
![]() $b \in \mathcal {T}/d$
, as desired.
$b \in \mathcal {T}/d$
, as desired.
Given the ease of proving Theorem 2.3, it is surprisingly more difficult when the denominators do have a common factor. In a follow-up to this current paper, we will translate the quotient operation into a geometric setting, which will allow us to generalise Theorem 2.3 to drop the ‘coprime denominators’ hypothesis. Intriguingly, the translation can cause a large blow-up in the numbers, for example,
Based on experimentation, this blow-up seems necessary.
3 Some families of numerical semigroups with full quotient rank
In this section, we produce two families of numerical semigroups: those in the first have embedding dimension
![]() $k+1$
but are not k-quotients, so in particular have full quotient rank (Theorem 3.1); and those in the second are not even intersections of k-quotients (Theorem 3.2).
$k+1$
but are not k-quotients, so in particular have full quotient rank (Theorem 3.1); and those in the second are not even intersections of k-quotients (Theorem 3.2).
Theorem 3.1. Given a positive integer k, let
![]() $a\ge 2^k$
be an integer. Define
$a\ge 2^k$
be an integer. Define
![]() $a_i=2a+2^i$
for
$a_i=2a+2^i$
for
![]() $i=0,1,\ldots ,k$
. Then the numerical semigroup
$i=0,1,\ldots ,k$
. Then the numerical semigroup
is not a k-quotient.
Proof. For
![]() $1\le j\le 2^k-1$
, let
$1\le j\le 2^k-1$
, let
![]() $b_j=\omega (\,j)a+j$
, where
$b_j=\omega (\,j)a+j$
, where
![]() $\omega (\,j)$
is the number of 1s in the binary representation of j. We first prove that if
$\omega (\,j)$
is the number of 1s in the binary representation of j. We first prove that if
![]() $\mathcal {T}$
is any k-quotient that contains
$\mathcal {T}$
is any k-quotient that contains
![]() $a_0,\ldots ,a_k$
(so
$a_0,\ldots ,a_k$
(so
![]() $\mathcal {T}=\mathcal {S}$
will be an example), then there exists j (
$\mathcal {T}=\mathcal {S}$
will be an example), then there exists j (
![]() $1\le j\le 2^k-1$
) such that
$1\le j\le 2^k-1$
) such that
![]() $b_j\in \mathcal {T}$
. Indeed, we apply Theorem 2.1. We know that there exists a nonempty
$b_j\in \mathcal {T}$
. Indeed, we apply Theorem 2.1. We know that there exists a nonempty
![]() $I\subseteq \{0,1,\ldots ,k\}$
such that
$I\subseteq \{0,1,\ldots ,k\}$
such that
![]() $a_I/2\in \mathcal {T}$
. If
$a_I/2\in \mathcal {T}$
. If
![]() $0\in I$
, then
$0\in I$
, then
![]() $a_I$
is odd and
$a_I$
is odd and
![]() $a_I/2$
is not an integer, so we know
$a_I/2$
is not an integer, so we know
![]() $I\subseteq \{1,\ldots ,k\}$
. Let
$I\subseteq \{1,\ldots ,k\}$
. Let
We have
![]() $1\le j\le 2^k-1$
, and
$1\le j\le 2^k-1$
, and
so
![]() $b_j\in \mathcal {T}$
.
$b_j\in \mathcal {T}$
.
Now we apply this to
![]() $\mathcal {T}=\mathcal {S}$
. Seeking a contradiction, suppose
$\mathcal {T}=\mathcal {S}$
. Seeking a contradiction, suppose
![]() $\mathcal {S}$
is a k-quotient, so that some
$\mathcal {S}$
is a k-quotient, so that some
![]() $b_j\in \mathcal {S}$
, that is,
$b_j\in \mathcal {S}$
, that is,
![]() $b_j=\sum _{i=0}^ka_ix_i$
with
$b_j=\sum _{i=0}^ka_ix_i$
with
![]() $x_i\in \mathbb {N}$
. Examining this sum modulo a, and noting that
$x_i\in \mathbb {N}$
. Examining this sum modulo a, and noting that
![]() $b_j=j\pmod a$
and
$b_j=j\pmod a$
and
![]() $a_i=2^i\pmod a$
, we see that
$a_i=2^i\pmod a$
, we see that
 $$ \begin{align*}\sum_{i=0}^k x_i\ge \omega(\,j).\end{align*} $$
$$ \begin{align*}\sum_{i=0}^k x_i\ge \omega(\,j).\end{align*} $$
However, a sum of
![]() $\omega (\,j)$
generators of
$\omega (\,j)$
generators of
![]() $\mathcal {S}$
is too large:
$\mathcal {S}$
is too large:
which is a contradiction. Therefore,
![]() $b_j\notin \mathcal {S}$
and so
$b_j\notin \mathcal {S}$
and so
![]() $\mathcal {S}$
cannot be a k-quotient.
$\mathcal {S}$
cannot be a k-quotient.
Theorem 3.2. Given a positive integer
![]() $k\ge 2$
, let
$k\ge 2$
, let
![]() $a\ge k2^k$
be an integer. As before, define
$a\ge k2^k$
be an integer. As before, define
![]() $a_i=2a+2^i$
and
$a_i=2a+2^i$
and
![]() $b_j=\omega (\,j)a+j$
, where
$b_j=\omega (\,j)a+j$
, where
![]() $\omega (\,j)$
is the number of 1s in the binary representation of j. Let
$\omega (\,j)$
is the number of 1s in the binary representation of j. Let
![]() $N=(2k+1)a$
. Then,
$N=(2k+1)a$
. Then,
cannot be written as an intersection of k-quotients.
Proof. Suppose, seeking a contradiction, that
![]() $\mathcal {S}=\bigcap _{\ell =1}^p \mathcal {S}_\ell $
, where the
$\mathcal {S}=\bigcap _{\ell =1}^p \mathcal {S}_\ell $
, where the
![]() $\mathcal {S}_\ell $
are k-quotients. Each
$\mathcal {S}_\ell $
are k-quotients. Each
![]() $\mathcal {S}_\ell $
must contain
$\mathcal {S}_\ell $
must contain
![]() $a_0,a_1,\ldots ,a_k$
, and we noted in the proof of Theorem 3.1 that this implies that
$a_0,a_1,\ldots ,a_k$
, and we noted in the proof of Theorem 3.1 that this implies that
![]() $\mathcal {S}_\ell $
must contain
$\mathcal {S}_\ell $
must contain
![]() $b_j$
for some j. However, then
$b_j$
for some j. However, then
![]() $\mathcal {S}_\ell $
contains both
$\mathcal {S}_\ell $
contains both
![]() $b_j$
and
$b_j$
and
![]() $N-b_j$
, and so additive closure implies that it contains N. This means
$N-b_j$
, and so additive closure implies that it contains N. This means
![]() $N \in \bigcap _{\ell =1}^p \mathcal {S}_\ell = \mathcal {S}$
. Let
$N \in \bigcap _{\ell =1}^p \mathcal {S}_\ell = \mathcal {S}$
. Let
 $$ \begin{align} N=\sum_{i=1}^k a_ix_i + \sum_{j=1}^{2^k-1}(N-b_j)y_j, \end{align} $$
$$ \begin{align} N=\sum_{i=1}^k a_ix_i + \sum_{j=1}^{2^k-1}(N-b_j)y_j, \end{align} $$
where
![]() $x_i,y_j \in \mathbb {N}$
. We break into three cases.
$x_i,y_j \in \mathbb {N}$
. We break into three cases.
-
• If
 $\sum _{j}y_j\ge 2$
, then (3.1) would be too large, as for some
$\sum _{j}y_j\ge 2$
, then (3.1) would be too large, as for some
 $j_1,j_2$
, which is impossible since
$j_1,j_2$
, which is impossible since $$ \begin{align*}(2k+1)a = N &\ge (N-b_{j_1})+(N-b_{j_2})\\ &= 2N-(\omega(j_1)+\omega(j_2))a -(j_1+j_2)\\ &> 2\cdot (2k+1)a -2ka-2\cdot 2^k\\ &= (2k+2)a-2^{k+1}, \end{align*} $$
$$ \begin{align*}(2k+1)a = N &\ge (N-b_{j_1})+(N-b_{j_2})\\ &= 2N-(\omega(j_1)+\omega(j_2))a -(j_1+j_2)\\ &> 2\cdot (2k+1)a -2ka-2\cdot 2^k\\ &= (2k+2)a-2^{k+1}, \end{align*} $$
 $a\ge 2^{k+1}$
.
$a\ge 2^{k+1}$
.
-
• If
 $\sum _{j}y_j=1$
, then (3.1) uses exactly one
$\sum _{j}y_j=1$
, then (3.1) uses exactly one
 $N-b_j$
. However, then
$N-b_j$
. However, then
 $N=(N-b_j)+b_j$
implies that
$N=(N-b_j)+b_j$
implies that
 $b_j\in \langle a_0,a_1\ldots ,a_k\rangle $
, which we saw was impossible in the proof of Theorem 3.1 since
$b_j\in \langle a_0,a_1\ldots ,a_k\rangle $
, which we saw was impossible in the proof of Theorem 3.1 since
 $a\ge 2^k$
.
$a\ge 2^k$
. -
• If
 $\sum _{j}y_j=0$
, then
$\sum _{j}y_j=0$
, then
 $N = \sum _{i} a_ix_i$
. If
$N = \sum _{i} a_ix_i$
. If
 $\sum _i x_i \le k$
, then which is impossible since
$\sum _i x_i \le k$
, then which is impossible since $$ \begin{align*}(2k+1)a=N\le k(2a+2^k),\end{align*} $$
$$ \begin{align*}(2k+1)a=N\le k(2a+2^k),\end{align*} $$
 $a>k2^k$
. However, if
$a>k2^k$
. However, if
 $\sum _i x_i> k$
, then which is also impossible.
$\sum _i x_i> k$
, then which is also impossible. $$ \begin{align*}(2k+1)a=N\ge (k+1)(2a+1)>(2k+1)a,\end{align*} $$
$$ \begin{align*}(2k+1)a=N\ge (k+1)(2a+1)>(2k+1)a,\end{align*} $$
In each case, we obtain a contradiction.
4 How often do numerical semigroups have full quotient rank?
In this section, we consider the question ‘how likely is a randomly selected numerical semigroup to have full quotient rank?’ We consider two sampling methods. The first is the ‘box’ method, wherein a fixed number of generators are selected uniformly and independently from an interval
![]() $[1,M]$
. Numerical semigroups selected under this model have high probability (that is, approaching 1 as
$[1,M]$
. Numerical semigroups selected under this model have high probability (that is, approaching 1 as
![]() $M \to \infty $
) of having full quotient rank.
$M \to \infty $
) of having full quotient rank.
Theorem 4.1. Fix a positive integer n. If
![]() $\mathcal {S} = \langle a_1, \ldots , a_n \rangle $
, where
$\mathcal {S} = \langle a_1, \ldots , a_n \rangle $
, where
![]() $a_1, \ldots , a_n \in [M]$
are uniformly and independently chosen, then the probability that
$a_1, \ldots , a_n \in [M]$
are uniformly and independently chosen, then the probability that
![]() $\mathcal {S}$
has full quotient rank tends to 1 as
$\mathcal {S}$
has full quotient rank tends to 1 as
![]() $M \to \infty $
. More precisely, this probability is
$M \to \infty $
. More precisely, this probability is
![]() $1 - O(M^{-{1}/{n}})$
.
$1 - O(M^{-{1}/{n}})$
.
Proof. By Corollary 2.2, it suffices to bound the probability that there exists
![]() $I \subseteq [n]$
such that
$I \subseteq [n]$
such that
![]() $a_I \in \langle a_j: j\notin I\rangle $
. Let A be this event, and let B be the event where
$a_I \in \langle a_j: j\notin I\rangle $
. Let A be this event, and let B be the event where
![]() $a_i \leq M^{{(n-1)}/{n}}$
for some i. We will use the fact that
$a_i \leq M^{{(n-1)}/{n}}$
for some i. We will use the fact that
For the first term, the union bound gives
For the second term, fix a nontrivial subset
![]() $I \subsetneq [n]$
and
$I \subsetneq [n]$
and
![]() $b_i \in \mathbb {N}$
for
$b_i \in \mathbb {N}$
for
![]() $i \notin I$
. If
$i \notin I$
. If
![]() $b_i> nM^{{1}/{n}}$
for some
$b_i> nM^{{1}/{n}}$
for some
![]() $i \notin I$
, then since every
$i \notin I$
, then since every
![]() $a_i$
is greater than
$a_i$
is greater than
![]() $M^{{(n-1)}/{n}}$
, we have
$M^{{(n-1)}/{n}}$
, we have
 $$ \begin{align*} \sum_{j \notin I} b_ja_j \geq b_ia_i> ( nM^{{1}/{n}} ) M^{{(n-1)}/{n}} = nM. \end{align*} $$
$$ \begin{align*} \sum_{j \notin I} b_ja_j \geq b_ia_i> ( nM^{{1}/{n}} ) M^{{(n-1)}/{n}} = nM. \end{align*} $$
However,
![]() $a_I$
cannot be this large because it is the sum of at most
$a_I$
cannot be this large because it is the sum of at most
![]() $n-1$
integers that are each at most M. So we need only consider
$n-1$
integers that are each at most M. So we need only consider
![]() $b_i \le nM^{{1}/{n}}$
. Letting
$b_i \le nM^{{1}/{n}}$
. Letting
![]() $i^\ast = \min (I)$
and
$i^\ast = \min (I)$
and
![]() $m = nM^{{1}/{n}}$
,
$m = nM^{{1}/{n}}$
,
 $$ \begin{align*} \Pr(A \mid B^c) &\le \sum_{\substack{I \subsetneq [n] \\ I \ne \emptyset}} \sum_{\substack{b_j \le m \\ j \notin I}} \Pr \bigg( \sum_{i \in I}a_i = \sum_{i \notin I}b_ia_i \biggm\vert a_1, \ldots, a_n> M^{{n}/{(n-1)}} \bigg) \\ & = \sum_{\substack{I \subsetneq [n] \\ I \ne \emptyset}} \sum_{\substack{b_j \le m \\ j \notin I}} \Pr \bigg( a_{i^\ast} = \sum_{i \notin I}b_ia_i - \!\!\! \sum_{i \in I \setminus \{i^\ast\}} \!\!\! a_i \biggm\vert a_1, \ldots, a_n > M^{{n}/{(n-1)}} \bigg) \\ & \le \sum_{\substack{I \subsetneq [n] \\ I \ne \emptyset}} \sum_{\substack{b_j \le m \\ j \notin I}} \frac{1}{M-M^{{(n-1)}/{n}}} \le \frac{( 2^n - 2) ( nM^{{1}/{n}})^{n-1}} {M-M^{{(n-1)}/{n}}} = \frac{( 2^n - 2 )n^{n-1}}{M^{{1}/{n}}-1}, \end{align*} $$
$$ \begin{align*} \Pr(A \mid B^c) &\le \sum_{\substack{I \subsetneq [n] \\ I \ne \emptyset}} \sum_{\substack{b_j \le m \\ j \notin I}} \Pr \bigg( \sum_{i \in I}a_i = \sum_{i \notin I}b_ia_i \biggm\vert a_1, \ldots, a_n> M^{{n}/{(n-1)}} \bigg) \\ & = \sum_{\substack{I \subsetneq [n] \\ I \ne \emptyset}} \sum_{\substack{b_j \le m \\ j \notin I}} \Pr \bigg( a_{i^\ast} = \sum_{i \notin I}b_ia_i - \!\!\! \sum_{i \in I \setminus \{i^\ast\}} \!\!\! a_i \biggm\vert a_1, \ldots, a_n > M^{{n}/{(n-1)}} \bigg) \\ & \le \sum_{\substack{I \subsetneq [n] \\ I \ne \emptyset}} \sum_{\substack{b_j \le m \\ j \notin I}} \frac{1}{M-M^{{(n-1)}/{n}}} \le \frac{( 2^n - 2) ( nM^{{1}/{n}})^{n-1}} {M-M^{{(n-1)}/{n}}} = \frac{( 2^n - 2 )n^{n-1}}{M^{{1}/{n}}-1}, \end{align*} $$
where the second inequality comes from the fact that for any choice of the
![]() $a_i$
with
$a_i$
with
![]() $i \neq i^\ast $
, there is at most one choice of
$i \neq i^\ast $
, there is at most one choice of
![]() $a_i^\ast $
that makes the linear equation hold. Thus,
$a_i^\ast $
that makes the linear equation hold. Thus,
which completes the proof.
Remark 4.2. The ‘minimally generated’ and ‘finite complement’ conditions, which are often imposed on numerical semigroups, do not affect Theorem 4.1. Indeed, under this ‘box’ probability model, the chosen generators
![]() $a_1, \ldots , a_n$
need not form a minimal generating set. Since the quotient rank is at most the embedding dimension, the (asymptotically rare) event that the rank of
$a_1, \ldots , a_n$
need not form a minimal generating set. Since the quotient rank is at most the embedding dimension, the (asymptotically rare) event that the rank of
![]() $\mathcal {S}$
is less than n contains the event that the chosen generating set is not minimal. Additionally, the probability that
$\mathcal {S}$
is less than n contains the event that the chosen generating set is not minimal. Additionally, the probability that
![]() $a_1,\ldots , a_n$
are relatively prime approaches the positive constant
$a_1,\ldots , a_n$
are relatively prime approaches the positive constant
![]() $1/\zeta (n)$
by [Reference Nymann15], where
$1/\zeta (n)$
by [Reference Nymann15], where
![]() $\zeta (n)$
is the Reimann zeta function
$\zeta (n)$
is the Reimann zeta function
![]() $\sum _{i=1}^{\infty }1/i^n$
. Therefore, even if one restricts to those
$\sum _{i=1}^{\infty }1/i^n$
. Therefore, even if one restricts to those
![]() $a_1,\ldots , a_n$
that are relatively prime, the conditional probability that the quotient rank of the resulting numerical semigroup is less than n still tends to 0.
$a_1,\ldots , a_n$
that are relatively prime, the conditional probability that the quotient rank of the resulting numerical semigroup is less than n still tends to 0.
Under the second model, a numerical semigroup
![]() $\mathcal {S}$
is selected uniformly at random from among the (finitely many) with a fixed smallest generator m and number of gaps g. Such numerical semigroups have high probability (that is, tending to 1 as
$\mathcal {S}$
is selected uniformly at random from among the (finitely many) with a fixed smallest generator m and number of gaps g. Such numerical semigroups have high probability (that is, tending to 1 as
![]() $g \to \infty $
) of having embedding dimension m (such numerical semigroups are said to have maximal embedding dimension). We prove that maximal embedding dimension numerical semigroups never have full quotient rank, illustrating a stark contrast in asymptotic behaviour to the first model.
$g \to \infty $
) of having embedding dimension m (such numerical semigroups are said to have maximal embedding dimension). We prove that maximal embedding dimension numerical semigroups never have full quotient rank, illustrating a stark contrast in asymptotic behaviour to the first model.
We first recall a characterisation of quotient rank 2 numerical semigroups, which appears in [Reference Rosales and García-Sánchez18] as a characterisation of proportionally modular numerical semigroups in the case
![]() $\gcd (\mathcal {S}) = 1$
. Our statement here is more general, thanks to Remark 1.3.
$\gcd (\mathcal {S}) = 1$
. Our statement here is more general, thanks to Remark 1.3.
Theorem 4.3. A numerical semigroup
![]() $\mathcal {S}$
with
$\mathcal {S}$
with
![]() $\gcd (\mathcal {S}) = D$
has quotient rank 2 if and only if there exists an ordering
$\gcd (\mathcal {S}) = D$
has quotient rank 2 if and only if there exists an ordering
![]() $b_1, \ldots , b_n$
of its minimal generators such that:
$b_1, \ldots , b_n$
of its minimal generators such that:
-
(a)
 $\gcd (b_i, b_{i+1}) = D$
for
$\gcd (b_i, b_{i+1}) = D$
for
 $1 \leq i \leq n-1$
; and
$1 \leq i \leq n-1$
; and -
(b)
 $b_{i-1} + b_{i+1}$
is divisible by
$b_{i-1} + b_{i+1}$
is divisible by
 $b_i$
for
$b_i$
for
 $2 \leq i \leq n-1$
.
$2 \leq i \leq n-1$
.
Lemma 4.4. For any
![]() $a, b, m \ge 1$
, the numerical semigroup
$a, b, m \ge 1$
, the numerical semigroup
![]() $\mathcal {S} = \langle m,am-1, bm+1 \rangle $
is a 2-quotient.
$\mathcal {S} = \langle m,am-1, bm+1 \rangle $
is a 2-quotient.
Proof. If
![]() $\mathsf e(\mathcal {S}) \le 2$
, then
$\mathsf e(\mathcal {S}) \le 2$
, then
![]() $\mathcal {S}$
is clearly a 2-quotient. Otherwise, letting
$\mathcal {S}$
is clearly a 2-quotient. Otherwise, letting
![]() $b_1 = am-1$
,
$b_1 = am-1$
,
![]() $b_2 = m$
and
$b_2 = m$
and
![]() $b_3 = bm+1$
, it is clear that
$b_3 = bm+1$
, it is clear that
![]() $\gcd (b_1, b_2) = \gcd (b_2, b_3) = 1$
and that
$\gcd (b_1, b_2) = \gcd (b_2, b_3) = 1$
and that
![]() ${b_2 \mid (b_1 + b_3)}$
. As such,
${b_2 \mid (b_1 + b_3)}$
. As such,
![]() $\mathcal {S}$
is a 2-quotient by Theorem 4.3.
$\mathcal {S}$
is a 2-quotient by Theorem 4.3.
Theorem 4.5. If
![]() $m = \min (\mathcal {S} \setminus \{0\})$
, then
$m = \min (\mathcal {S} \setminus \{0\})$
, then
![]() $\mathcal {S}$
is an
$\mathcal {S}$
is an
![]() $(m-1)$
-quotient. In particular, if
$(m-1)$
-quotient. In particular, if
![]() $\mathsf e(\mathcal {S}) = m$
, then
$\mathsf e(\mathcal {S}) = m$
, then
![]() $\mathcal {S}$
does not have full quotient rank.
$\mathcal {S}$
does not have full quotient rank.
Proof. If
![]() $\mathcal {S}={\mathcal {S}}/{1}$
has embedding dimension less than m, then the proof is immediate. If not, then
$\mathcal {S}={\mathcal {S}}/{1}$
has embedding dimension less than m, then the proof is immediate. If not, then
![]() $\mathcal {S}$
has m minimal generators, and so they must all have distinct residues modulo m. That is,
$\mathcal {S}$
has m minimal generators, and so they must all have distinct residues modulo m. That is,
for some positive integers
![]() $b_1, \ldots , b_{m-1}$
. Write
$b_1, \ldots , b_{m-1}$
. Write
![]() $\mathcal {S} = \mathcal {S}_1 + \mathcal {S}_2$
, where
$\mathcal {S} = \mathcal {S}_1 + \mathcal {S}_2$
, where
Now by Lemma 4.4,
![]() $\mathcal {S}_1$
as a 2-quotient, and
$\mathcal {S}_1$
as a 2-quotient, and
![]() $\mathcal {S}_2 = {\mathcal {S}_2}/{1}$
is trivially an
$\mathcal {S}_2 = {\mathcal {S}_2}/{1}$
is trivially an
![]() $(m-3)$
-quotient. Since
$(m-3)$
-quotient. Since
![]() $1$
is coprime to every integer, Theorem 2.3 implies
$1$
is coprime to every integer, Theorem 2.3 implies
![]() $\mathcal {S}$
is an
$\mathcal {S}$
is an
![]() $(m-1)$
-quotient.
$(m-1)$
-quotient.
Acknowledgements
The authors thank Pedro García-Sánchez, John Goodrick and Francesco Strazzanti for helpful conversations.